Een asymptoot is een lijn die een grafiek nadert, maar niet snijdt.
In deze les leren we hoe we verticale asymptoten, horizontale asymptoten en schuine asymptoten van rationale functies kunnen vinden.
Onderwerpen die hiermee verband houden:
Meer lessen over Rekenen

Het volgende diagram toont de verschillende soorten asymptoten: horizontale asymptoten, verticale asymptoten, en schuine asymptoten. Scroll naar beneden voor meer voorbeelden en oplossingen voor het vinden van asymptoten.

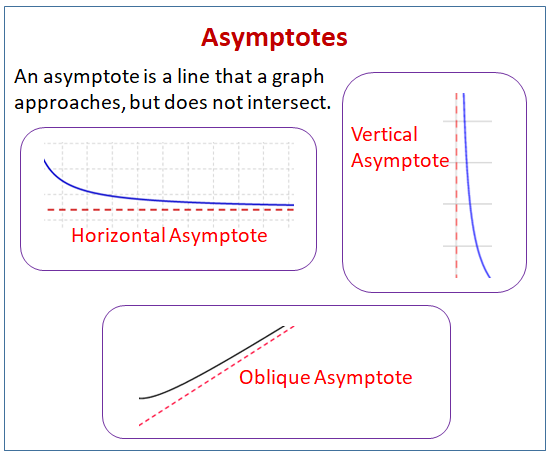
Hoe bepaal je de verticale asymptoot?

Methode 1: Gebruik de definitie van verticale asymptoot

De lijn x = a wordt een verticale asymptoot van de kromme y = f(x) genoemd als ten minste een van de volgende beweringen waar is.

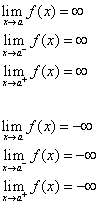
Methode 2:

Voor rationale functies zijn verticale asymptoten verticale lijnen die overeenkomen met de nulpunten van de noemer.
Gegeven de rationale functie, f(x)

Stap 1: schrijf f(x) in gereduceerde vorm

Stap 2: als x – c een factor is in de noemer dan is x = c de verticale asymptoot.

Voorbeeld:

Vind de verticale asymptoten van

Oplossing:

Methode 1: Gebruik de definitie van Verticale asymptoot.

Als x dicht bij 3 ligt maar groter is dan 3, dan is de noemer x – 3 een klein positief getal en 2x ligt dicht bij 8. is dus een groot positief getal.

Intuïtief zien we dat

Zo ook, als x dicht bij 3 ligt maar kleiner is dan 3, dan is x – 3 een klein negatief getal en 2x ligt dicht bij 8. is dus een groot negatief getal.

De lijn x = 3 is de verticale asymptoot.

Methode 2:

Stap 1: f(x) is al in gereduceerde vorm.

Stap 2: De noemer is x – 3, en dus ligt de verticale asymptoot bij x = 3.

Vinden van verticale asymptoten van rationale functies

Waar moet je op letten om verticale asymptoten van rationale functies te vinden.

• Stapsgewijze oplossingen tonen

Verticale asymptoten van rationale functies: Quick Way to Find Them

Voorbeeld van het vinden van verticale asymptoten van rationale functies.

• Show Step-by-step Solutions

Hoe vind je verticale asymptoten voor rationale functies

• Show Step-by-step Solutions

Hoe bepaal je de horizontale asymptoot?

Methode 1: Gebruik de definitie van Horizontale Asymptoot

De lijn y = L wordt een horizontale asymptoot van de kromme y = f(x) genoemd indien ofwel

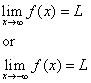
Methode 2:

Voor de rationale functie, f(x)

Als de graad van x in de teller kleiner is dan de graad van x in de noemer dan is y = 0 de horizontale asymptoot.

Als de graad van x in de teller gelijk is aan de graad van x in de noemer dan is y = c waarbij c wordt verkregen door de voorloopcoëfficiënten te delen.

Voorbeeld:

Vind de horizontale en verticale asymptoten van de functie.

Oplossing:

Methode 1:

Deel zowel teller als noemer door x.

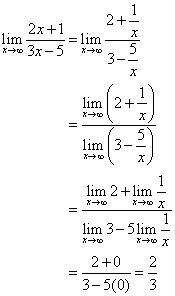
De lijn is de horizontale asymptoot.

Methode 2:

De graad van x in de teller is gelijk aan de graad van x in de noemer.

Deling van de leidende coëfficiënten levert

De lijn is de horizontale asymptoot.

Shortcut to Find Horizontal Asymptotes of Rational Functions

Een paar trucs die het vinden van horizontale asymptoten van rationale functies heel gemakkelijk maken

• Show Step-by-step Solutions

Deze video geeft een basisoverzicht van horizontale asymptoten. We zullen bepalen of de gegeven rationale functies horizontale asymptoten hebben en wat ze zijn.

• Show Step-by-step Solutions

Deze video gaat dieper in op horizontale asymptootregels.

• Show Step-by-step Solutions

Oblique Asymptote or Slant Asymptote

Sommige krommen hebben asymptoten die schuin zijn, dat wil zeggen, noch horizontaal, noch verticaal.

Als dan wordt de rechte y = mx + b de schuine of schuine asymptoot genoemd omdat de verticale afstanden tussen de kromme y = f(x) en de rechte y = mx + b 0 benaderen.

Voor rationale functies komen schuine asymptoten voor als de graad van de teller één meer is dan de graad van de noemer. In zo’n geval kan de vergelijking van de schuine asymptoot worden gevonden door een lange deling.

Voorbeeld:

Vind de asymptoten van de functie

Oplossing:

Omdat de noemer x2 + 1 nooit 0 is, is er geen verticale asymptoot.

Omdat de graad van x in de teller groter is dan de graad van x in de noemer is er geen horizontale asymptoot.

Omdat de graad van x in de teller één groter is dan de graad van x in de noemer kunnen we lange deling gebruiken om de schuine asymptoot te verkrijgen.

De rechte y = x is dus de schuine asymptoot.

Vinden van schuine asymptoten van rationale functies

Deze video beschrijft wanneer een rationale functie een schuine asymptoot heeft, beschrijft kort wat een schuine asymptoot is, en geeft vervolgens twee voorbeelden.

• Stapsgewijze oplossingen tonen

Vind asymptoten van een rationale functie (verticaal, horizontaal en schuin/schuin)

Deze video laat zien hoe je de verticale asymptoten en een schuine/schuine asymptoot van een rationale functie kunt vinden.

• Stapsgewijze oplossingen tonen

Alle asymptoten van een rationale functie vinden (verticaal, horizontaal, schuin)

Hier bekijken we een functie en vinden we de verticale asymptoot en concluderen ook dat er geen horizontale asymptoten zijn, maar dat er wel een schuine asymptoot bestaat. We gebruiken dan lange deling om de schuine asymptoot te vinden.

• Laat stap-voor-stap oplossingen zien

Probeer met de gratis Mathway rekenmachine en probleemoplosser hieronder om verschillende wiskunde onderwerpen te oefenen. Probeer de gegeven voorbeelden, of typ uw eigen probleem in en controleer uw antwoord met de stap-voor-stap uitleg.