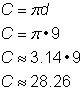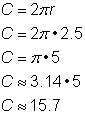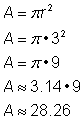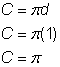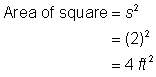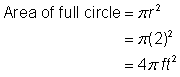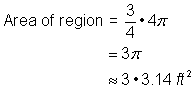cirkels
Leerdoel(en)
– Eigenschappen van cirkels benoemen.
– De omtrek van een cirkel bepalen.
– De oppervlakte van een cirkel bepalen.
– De oppervlakte en omtrek van samengestelde meetkundige figuren bepalen.
Inleiding
Cirkels zijn een veel voorkomende vorm. Je ziet ze overal: wielen van auto’s, frisbees die door de lucht vliegen, compact discs die gegevens overbrengen. Dit zijn allemaal cirkels.
Een cirkel is een tweedimensionale figuur, net als veelhoeken en vierhoeken. Cirkels worden echter anders gemeten dan deze andere vormen – je moet zelfs andere termen gebruiken om ze te beschrijven. Laten we eens kijken naar deze interessante vorm.
Eigenschappen van cirkels
Een cirkel stelt een verzameling punten voor, die allemaal op dezelfde afstand liggen van een vast, middelpunt. Dit vaste punt wordt het middelpunt genoemd. De afstand van het middelpunt van de cirkel tot een willekeurig punt op de cirkel wordt de straal genoemd.
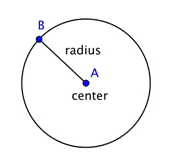
Wanneer twee stralen (het meervoud van straal) worden samengevoegd tot een lijnstuk over de cirkel, heb je een diameter. De diameter van een cirkel gaat door het middelpunt van de cirkel en heeft zijn eindpunten op de cirkel zelf.
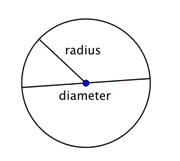
De diameter van een willekeurige cirkel is twee keer de lengte van de straal van die cirkel. Hij kan worden weergegeven met de uitdrukking 2r, of “twee keer de straal”. Dus als u de straal van een cirkel kent, kunt u die met 2 vermenigvuldigen om de diameter te vinden; dit betekent ook dat als u de diameter van een cirkel kent, u door 2 kunt delen om de straal te vinden.
|
Voorbeeld |
||
|
Probleem |
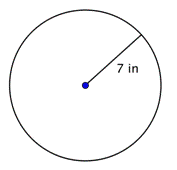
Vind de diameter van de cirkel.
|
|
|
d = 2r d = 2(7) d = 14 |
De diameter is twee keer de straal, oftewel 2r. De straal van deze cirkel is 7 inch, dus de diameter is 2(7) = 14 inch. |
|
|
Antwoord |
De diameter is 14 inch. |
|
|
Voorbeeld |
||
|
Probleem |
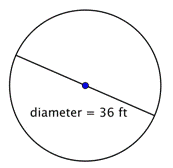
Vind de straal van de cirkel.
|
|
|
|
De straal is de helft van de diameter, ofwel |
|
|
Antwoord |
De straal is 18 voet. |
|
Omtrek
De afstand om een cirkel wordt de omtrek genoemd. (Bedenk dat de afstand om een veelhoek de omtrek is.)
Een interessante eigenschap van cirkels is dat de verhouding tussen de omtrek en de diameter van een cirkel voor alle cirkels gelijk is. Het maakt niet uit hoe groot de cirkel is, de verhouding tussen de omtrek en de diameter zal hetzelfde zijn.
Hieronder staan enkele actuele metingen van verschillende voorwerpen. De metingen zijn nauwkeurig tot op de millimeter of kwart inch (afhankelijk van de gebruikte meeteenheid). Kijk naar de verhouding van de omtrek tot de diameter voor elk van hen – hoewel de items zijn verschillend, de verhouding voor elk is ongeveer hetzelfde.
|
Item |
Omtrek (C) (afgerond op het dichtstbijzijnde honderdste) |
Diameter (d) |
Ratio |
|
Cup |
253 mm |
79 mm |
|
|
Quarter |
84 mm |
27 mm |
|
|
Bowl |
37.25 in |
11.75 in |
|
De omtrek en de diameter zijn benaderende maten, aangezien er geen precieze manier is om deze afmetingen exact te meten. Als u ze echter nauwkeuriger zou kunnen meten, zou u zien dat de verhouding ![]() voor elk van de gegeven items in de richting van 3,14 zou gaan. De wiskundige naam voor de verhouding
voor elk van de gegeven items in de richting van 3,14 zou gaan. De wiskundige naam voor de verhouding ![]() is pi, en wordt weergegeven door de Griekse letter
is pi, en wordt weergegeven door de Griekse letter ![]() .
.
![]() is een niet-beëindigende, niet-herhalende decimaal, dus het is onmogelijk om het volledig uit te schrijven. De eerste 10 cijfers van
is een niet-beëindigende, niet-herhalende decimaal, dus het is onmogelijk om het volledig uit te schrijven. De eerste 10 cijfers van ![]() zijn 3,141592653; het wordt vaak afgerond tot 3,14 of geschat als de breuk
zijn 3,141592653; het wordt vaak afgerond tot 3,14 of geschat als de breuk ![]() . Merk op dat zowel 3,14 als
. Merk op dat zowel 3,14 als ![]() benaderingen zijn van
benaderingen zijn van![]() , en worden gebruikt in berekeningen waarbij het niet belangrijk is om precies te zijn.
, en worden gebruikt in berekeningen waarbij het niet belangrijk is om precies te zijn.
Omdat je weet dat de verhouding tussen omtrek en diameter (of ![]() ) consistent is voor alle cirkels, kun je dit getal gebruiken om de omtrek van een cirkel te vinden als je de diameter kent.
) consistent is voor alle cirkels, kun je dit getal gebruiken om de omtrek van een cirkel te vinden als je de diameter kent.
![]() =
= ![]() , dus C =
, dus C = ![]() d
d
Ook, omdat d = 2r, dan is C = ![]() d =
d = ![]() (2r) = 2
(2r) = 2![]() r.
r.
Omtrek van een cirkel
Om de omtrek (C) van een cirkel te vinden, gebruikt u een van de volgende formules:
Als u de diameter (d) van een cirkel weet: ![]()
Als je de straal (r) van een cirkel weet: ![]()
|
Voorbeeld |
||
|
Probleem |
Vind de omtrek van de cirkel.
|
|
|
|
Om de omtrek te berekenen bij een diameter van 9 inch, gebruikt u de formule Omdat u een benadering gebruikt voor |
|
|
Antwoord |
De omtrek is 9 |
|
|
Voorbeeld |
||
|
Opgave |
Vind de omtrek van een cirkel met een straal van 2.5 yards. |
|
|
|
Om de omtrek van een cirkel met een straal van 2,5 yards te berekenen, gebruikt u de formule |
|
|
Antwoord |
De omtrek is 5 |
|
Een cirkel heeft een straal van 8 inches. Wat is de omtrek, afgerond op de dichtstbijzijnde inch?
A) 25 inch
B) 50 inch
C) 64 inch2
D) 201 inch
Area
![]() is een belangrijk getal in de meetkunde. Je hebt het al gebruikt om de omtrek van een cirkel te berekenen. Je gebruikt
is een belangrijk getal in de meetkunde. Je hebt het al gebruikt om de omtrek van een cirkel te berekenen. Je gebruikt ![]() ook bij het berekenen van de oppervlakte van een cirkel.
ook bij het berekenen van de oppervlakte van een cirkel.
Area of a Circle
Om de oppervlakte (A) van een cirkel te vinden, gebruik je de formule: ![]()
|
Voorbeeld |
||
|
Probleem |
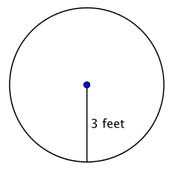
Vind de oppervlakte van de cirkel.
|
|
|
|
Om de oppervlakte van deze cirkel te vinden, gebruikt u de formule Denk eraan het antwoord te schrijven in termen van kwadraateenheden, omdat u de oppervlakte vindt. |
|
|
Antwoorden |
De oppervlakte is 9 |
|
Een knoop heeft een doorsnede van 20 millimeter. Wat is de oppervlakte van de knoop? Gebruik 3,14 als benadering van ![]() .
.
A) 62,8 mm
B) 314 mm2
C) 400 mm2
D) 1256 mm2
Samengestelde figuren
Nu je weet hoe je de omtrek en oppervlakte van een cirkel kunt berekenen, kun je deze kennis gebruiken om de omtrek en oppervlakte van samengestelde figuren te vinden. De truc om dit soort problemen op te lossen is om vormen (en delen van vormen) binnen de samengestelde figuur te identificeren, hun individuele afmetingen te berekenen, en ze dan bij elkaar op te tellen.
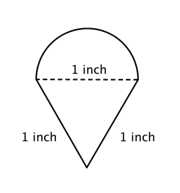
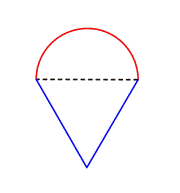
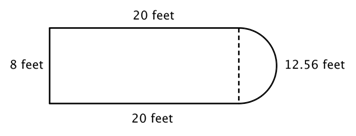
Kijk bijvoorbeeld eens naar de afbeelding hieronder. Is het mogelijk om de omtrek te vinden?
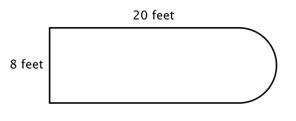
De eerste stap is om eenvoudigere figuren binnen deze samengestelde figuur te identificeren. Je kunt het opdelen in een rechthoek en een halve cirkel, zoals hieronder te zien is.
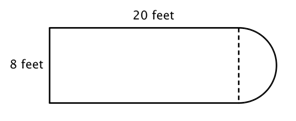
Je weet hoe je de omtrek van een rechthoek kunt vinden, en je weet hoe je de omtrek van een cirkel kunt vinden. Hier is de omtrek van de drie zijden van de rechthoek 8 + 20 + 20 = 48 voet. (Merk op dat slechts drie zijden van de rechthoek worden opgeteld bij de omtrek van de samengestelde figuur, omdat de andere zijde niet aan een rand ligt; deze wordt bedekt door de halve cirkel!)
Om de omtrek van de halve cirkel te vinden, gebruikt u de formule ![]() met een diameter van 8 voet, en dan neemt u de helft van de uitkomst. De omtrek van de halve cirkel is
met een diameter van 8 voet, en dan neemt u de helft van de uitkomst. De omtrek van de halve cirkel is ![]() , of ongeveer 12,56 voet, dus de totale omtrek is ongeveer 60,56 voet.
, of ongeveer 12,56 voet, dus de totale omtrek is ongeveer 60,56 voet.
|
Voorbeeld |
||||
|
Probleem |
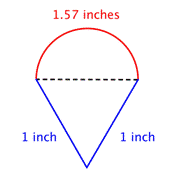
Vind de omtrek (op het dichtstbijzijnde honderdste) van de samengestelde figuur, die bestaat uit een halve cirkel en een driehoek.
|
|||
|
|
Identificeer kleinere vormen binnen de samengestelde figuur. Deze figuur bevat een halve cirkel en een driehoek. |
|||
|
Diameter (d) = 1
Omtrek van halve cirkel = |
Vind de omtrek van de cirkel. Deel vervolgens door 2 om de omtrek van de halve cirkel te vinden. |
|||
|
|
|
Vind de totale omtrek door de omtrek van de halve cirkel en de lengtes van de twee benen bij elkaar op te tellen. Omdat onze meting van de omtrek van de halve cirkel bij benadering is, zal de omtrek ook een benadering zijn. |
||
|
Antwoord |
Bijna 3,5 cm |
Bijna 3,5 cm |
Bereken de omtrek van de halve cirkel.57 inch |
|
|
Voorbeeld |
||
|
Probleem |
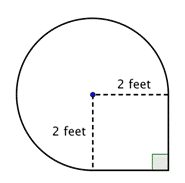
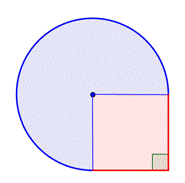
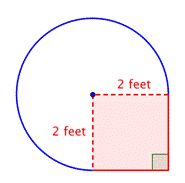
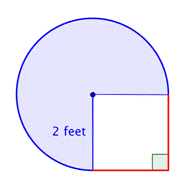
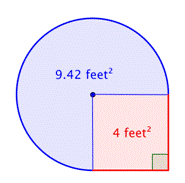
Bepaal de oppervlakte van het samengestelde figuur, bestaande uit driekwart cirkel en vierkant, tot op een honderdste nauwkeurig.
|
|
|
|
Benoem kleinere vormen binnen de samengestelde figuur. Deze figuur bevat een cirkelvormig gebied en een vierkant. Als u de oppervlakte van elk vindt, kunt u de oppervlakte van de hele figuur vinden. |
|
|
|
Vind de oppervlakte van het vierkant. |
|
|
|
|
Vind de oppervlakte van het cirkelvormige gebied. De straal is 2 voet. Merk op dat het gebied |
|
|
4 voet2 + |
Tel de twee gebieden bij elkaar op. Aangezien uw meting van de oppervlakte van de cirkel bij benadering is, zal de oppervlakte van de figuur ook een benadering zijn. |
|
Antwoord |
De oppervlakte is ongeveer 13.42 voet2. |
|
Wat is de oppervlakte (op een honderdste nauwkeurig) van de figuur hieronder? (Beide afgeronde gebieden zijn halve cirkels.)
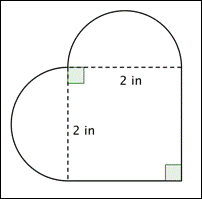
A) 16,56 in2
B) 7,14 in2
C) 4 in2
D) 3,14 in2
Samenvatting
Cirkels zijn een belangrijke meetkundige vorm. De afstand rond een cirkel wordt de omtrek genoemd, en de binnenruimte van een cirkel wordt de oppervlakte genoemd. Voor de berekening van de omtrek en de oppervlakte van een cirkel is een getal nodig dat pi (![]() ) heet, en dat een niet-afbrekend, niet-herhalend decimaal getal is. Pi wordt vaak benaderd met de waarden 3,14 en
) heet, en dat een niet-afbrekend, niet-herhalend decimaal getal is. Pi wordt vaak benaderd met de waarden 3,14 en ![]() . U kunt de omtrek of oppervlakte van samengestelde vormen vinden – met inbegrip van vormen die cirkelvormige doorsneden bevatten – door waar nodig de omtrek- en oppervlakteformules toe te passen.
. U kunt de omtrek of oppervlakte van samengestelde vormen vinden – met inbegrip van vormen die cirkelvormige doorsneden bevatten – door waar nodig de omtrek- en oppervlakteformules toe te passen.