Wat volgt is mijn kijk op enkele wiskundeproblemen van zogenaamde “common core math” of “nieuwe wiskunde” die op het internet de ronde hebben gedaan. Ik vind dat ze een verkeerde implementatie van de CCS laten zien.

Bedenk dat niet alles wat je in wiskundeboeken of op het internet ziet, correct wordt gedaan op basis van de CCS. In sommige van de voorbeelden die je ziet, lijkt het alsof mensen hun gezond verstand overboord gooien bij het maken van wiskundeproblemen om aan de gemeenschappelijke kernnormen te voldoen!

Het verbaast me niet dat de implementatie op sommige plaatsen is “verknoeid”. De CCS zijn zo’n verandering voor de meeste leraren dat ze veel ondersteuning en her-educatie nodig hebben voordat ze er les aan moeten geven.

Ik heb altijd gedacht dat het VOORNAAMSTE probleem van het wiskunde-onderwijs in de lagere klassen op openbare scholen is dat veel leraren in het lager onderwijs wiskunde niet voldoende begrijpen om het zelfs op elementair niveau goed te kunnen onderwijzen. Velen van hen begrijpen bijvoorbeeld niet de concepten, het waarom en de waarom van de algoritmen die zij onderwijzen. Dat is niet hun schuld – het probleem is terug te voeren op wat hun op de lerarenopleiding en in hun eigen schoolopleiding is geleerd.

Ook het normdocument zelf is hier en daar wat moeilijk te volgen. Het lezen ervan vereist enig denkwerk. Ik zou willen dat iemand een boekje maakte waarin de normen in eenvoudige taal en met tal van voorbeelden worden uitgelegd.

Slechte voorbeelden van “common core” of “nieuwe wiskunde”

Voorbeeld 1

Onlangs zag ik op Facebook een afbeelding van aftrekstrategieën waarvan beweerd werd dat het uit een wiskundeboek van de 1e klas kwam en “Common Core wiskunde” was.”

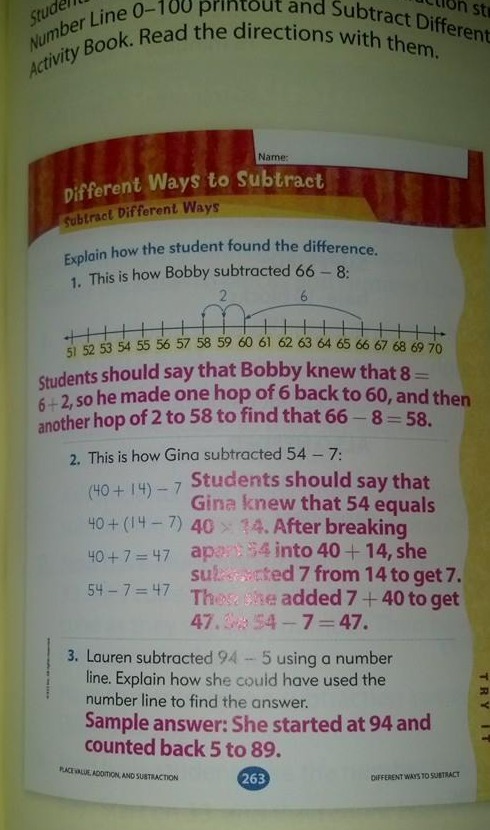
Ik denk dat methode 2 veel te moeilijk is voor de eerste klas, en ik zou zelfs methode 1 voor de tweede klas laten staan.

Hoe dan ook, dat boek lijkt niet eens te stroken met de Common Core standaarden. De normen voor de 1e klas bevatten dit soort aftrekproblemen gewoon niet!

Dit is wat we vinden in de normen:

Tellen en aftrekken binnen 20.
1.OA.5
Tellen relateren aan optellen en aftrekken (bijv. door bij 2 te tellen om er 2 bij te tellen).
1.OA.6.
Tellen en aftrekken binnen 20 en daarbij laten zien dat hij vloeiend kan optellen en aftrekken binnen 10. Gebruik maken van strategieën zoals tellen; tientallen maken (bijv. 8 + 6 = 8 + 2 + 4 = 10 + 4 = 14); een getal ontbinden tot een tiental (bijv. 13 – 4 = 13 – 3 – 1 = 10 – 1 = 9); gebruik maken van de relatie tussen optellen en aftrekken (bijv. wetende dat 8 + 4 = 12, weet men dat 12 – 8 = 4); en gelijkwaardige maar gemakkelijkere of bekende sommen maken (bijv, 6 + 7 optellen door het bekende equivalent 6 + 6 + 1 = 12 + 1 = 13 te maken).

Het schoolvoorbeeld lijkt in te willen gaan op 1.OA.6 hierboven, maar dat is duidelijk voor het optellen en aftrekken binnen 20, niet met grotere getallen.

Later in de normen voor de 1e klas zien we twee normen die te maken hebben met het aftrekken van getallen van twee cijfers (binnen 100):

1.NBT.5.
Gegeven een getal van twee cijfers, mentaal 10 meer of 10 minder vinden dan het getal, zonder te hoeven tellen; de gebruikte redenering uitleggen.
1.NBT.6.
Trek veelvouden van 10 in het bereik 10-90 af van veelvouden van 10 in het bereik 10-90 (positieve of nulverschillen), met behulp van concrete modellen of tekeningen en strategieën gebaseerd op plaatswaarde, eigenschappen van bewerkingen, en/of het verband tussen optellen en aftrekken; relateer de strategie aan een geschreven methode en leg de gebruikte redenering uit.
Maria’s noot: dit betekent aftrekkingen zoals 34 – 20 of 89 – 60.

maar geen van beide omvat aftrekkingen zoals 54 – 7 of 82 – 6. Die zitten in de 2e klas:

2.NBT.5
Vlot optellen en aftrekken binnen 100 met behulp van strategieën gebaseerd op plaatswaarde, eigenschappen van operaties, en/of het verband tussen optellen en aftrekken.

Merk op dat de norm voor de tweede klas niet specificeert HOE je aftrekt (of je mentale rekenstrategieën gebruikt of getallen onder elkaar schrijft en leent/groepeert).

Voorbeeld 2

Van Houghton Mifflin, zogenaamd:

Juanita wil zakjes met stickers aan haar vrienden geven. Ze wil aan elke vriend hetzelfde aantal stickers geven. Ze weet niet zeker of ze 4 zakken of 6 zakken stickers nodig heeft. Hoeveel stickers kan ze kopen zodat er geen stickers overblijven?

Het stickerprobleem heeft te maken met het concept van het kleinste gemene veelvoud (LCM). (Het antwoord is dat ze 12, 24, 36, of een ander veelvoud van 12 stickers moet kopen, want dan kan ze ze ofwel in 4 zakjes ofwel in 6 zakjes verdelen.)

Zeker, het probleem is ZEER onduidelijk en slecht geformuleerd. Mijn gok is dat het boekje waarin dit staat gewoon niet is geredigeerd. Het is niet de schuld van de normen zelf. Ik ben het eens met Bart Goddard op Math Forum. Dit is een symptoom van de blinde haast om “real-life” verhaal problemen te produceren die uiteindelijk onzinnig blijken te zijn.

Uit het PDF-document maak ik op dat het probleem voor de vierde klas is, omdat alle andere woordproblemen in het boekje voldoen aan de normen voor de vierde klas (factoren, priemgetallen). Maar in de CCS staat het kleinste gemene veelvoud niet eens in de normen voor de vierde klas (het staat in de zesde)!!! Er is echt iets misgegaan met dat woordprobleem.

Voorbeeld 3

Wederom, zogenaamd van Houghton Mifflin voor de 1e klas. Dit komt overeen met de norm die ik hierboven al heb geciteerd:

Optellen en aftrekken binnen 20.
1.OA.6.
Toevoegen en aftrekken binnen 20, vloeiend aantonen voor optellen en aftrekken binnen 10. Strategieën gebruiken zoals doortellen; tiental maken (bijv. 8 + 6 = 8 + 2 + 4 = 10 + 4 = 14); een getal ontbinden dat leidt tot een tiental (bijv. 13 – 4 = 13 – 3 – 1 = 10 – 1 = 9); de relatie tussen optellen en aftrekken gebruiken (bijv, wetende dat 8 + 4 = 12, weet men dat 12 – 8 = 4); en het maken van gelijkwaardige maar gemakkelijkere of bekende sommen (bijv. 6 + 7 optellen door het bekende equivalent 6 + 6 + 1 = 12 + 1 = 13 te maken).

Nou, allereerst, de strategie van “een tiental maken” heeft te maken met TOEVOEGEN, niet met aftrekken. Bij aftrekken heet dat “ontleden van een getal dat leidt tot een tien”. Dus de opdracht zou moeten luiden: “Wat is een manier om een getal te ontbinden dat tot een tien leidt?” Ik vind het volslagen onzin om van leerlingen uit de eerste klas te eisen dat ze die terminologie kennen.

Maar er is nog een probleem. Als u werkelijk alle normen leest, zult u merken dat op verschillende andere plaatsen wordt gevraagd de gebruikte redenering uit te leggen of een bepaalde visuele methode in verband te brengen met de strategie, maar NIET in deze norm!

De manier waarop ik deze norm zie, is dat leraren worden verondersteld de verschillende genoemde strategieën te onderwijzen en vervolgens de leerlingen SIMPELE optel- en aftrekproblemen binnen 20 te geven, zoals 15 – 8 en 10 – 6. Ik zie NIET dat deze norm vereist dat leerlingen herkennen of een bepaald visueel model overeenkomt met een bepaalde strategie.

Het lijkt er weer op dat de auteur het gezonde verstand overboord gooit… en de normen eigenlijk niet begrijpt.

Voorbeeld 4

Het voorbeeld hieronder is erg slecht geformuleerd, maar het CONCEPT erachter is erg goed en is ook te vinden in Math Mammoth. Ik kan dus wel achterhalen wat ze willen.

Je ziet vijf vierkanten. Kleur sommige blauw en de rest rood. Dat is duidelijk.

Kleur dan de vierkanten in de “nummerband” op dezelfde manier. De nummerband gaat naar die drie cirkels. Een kind dat aanwezig is geweest in een les waar de leraar getallenbanden leert, weet hopelijk wat het betekent. Het is hetzelfde concept als een feitenfamilie… het bovenste getal is de som of het totaal (5), en de getallen die naar de onderste cirkels gaan, corresponderen met hoeveel je er blauw en hoeveel rood hebt gekleurd, in dit geval 1 en 4.

Dan denk ik dat de verborgen partners ook de 1 en 4 zijn. Laat 1 en 4 vingers aan een volwassene zien. Kleur als laatste de vingers 1 en 4 in het plaatje (en niet je eigen vingers zoals het klinkt).

Het gedeelte over de vingers is naar mijn mening overbodig en verwarrend. Het concept van getalbanden is echter veel ouder dan de CCS. Getallenbruggen worden in feite niet genoemd in de CCS, hoewel ze wel verband houden met deze norm:

1.OA.4
Ontdek aftrekken als een onbekend-toegevoegd probleem. Bijvoorbeeld, trek 10 – 8 af door het vinden van het getal dat 10 maakt wanneer het wordt opgeteld bij 8.

en met deze

1.OA.6.
Toevoegen en aftrekken binnen 20, waarbij vloeiend optellen en aftrekken binnen 10 wordt getoond.

Ik weet niet waarom dat werkblad met getalverbindingen wordt gegeven als een voorbeeld van Common Core Math. Het zou veel beter getiteld zijn als een voorbeeld van een slecht geformuleerd wiskundewerkblad dat zelfs van vóór de Common Core zou kunnen dateren (en dat gewoon in dit specifieke leerplan wordt hergebruikt)… want zoals ik al zei, worden getallenbruggen NIET vermeld in de CCS.

Wat Common Core Wiskundestandaarden niet zijn

1. Ze zijn geen “nieuwe wiskunde”. Vergeleken met veel wiskundecurricula uit de jaren 2000, die de nadruk legden op niet-traditionele algoritmen, is CCS een duidelijke stap in de richting van traditionele algoritmen en memorisatie. Kijk eens naar deze specifieke normen:
   

   2.OA.2
   Vlot optellen en aftrekken binnen 20 met behulp van mentale strategieën. Tegen het einde van Grade 2, weet uit het hoofd alle sommen van twee een-cijferige getallen.
   Maria’s noot: dit zijn uw basis optelfeiten, zoals 7 + 7 of 5 + 4.

   3.OA.7
   Vlot vermenigvuldigen en delen binnen 100, gebruikmakend van strategieën zoals het verband tussen vermenigvuldigen en delen (bijvoorbeeld, wetend dat 8 × 5 = 40, weet men dat 40 ÷ 5 = 8) of eigenschappen van bewerkingen. Tegen het einde van graad 3, kent men uit het hoofd alle producten van twee eencijferige getallen.
   Maria’s noot: dit betekent tafels van vermenigvuldiging en basis delingsfeiten.

   4.NBT.4
   Vlot optellen en aftrekken van gehele getallen van meerdere cijfers met behulp van het standaardalgoritme.

   5.NBT.5
   Vlot vermenigvuldigen van gehele getallen van meerdere cijfers met behulp van het standaardalgoritme.
   Maria’s noot: dit betekent niet dat leerlingen alleen in de 5e klas vermenigvuldigen van gehele getallen van meerdere cijfers; dat wordt ook in de 3e en 4e klas bestudeerd.

2. De normen leggen geen vreemde strategieën of visuele modellen op aan leraren en leerlingen. Veel normen laten het aan de leraren en leerlingen over. Bijvoorbeeld:
   

   2.NBT.5
   Vlot optellen en aftrekken binnen 100 met behulp van strategieën gebaseerd op plaatswaarde, eigenschappen van bewerkingen, en/of het verband tussen optellen en aftrekken.

   Let op de “en/of” in de bovenstaande zin. Dit betekent dat de leerkrachten en de leerlingen NIET beperkt worden tot het gebruik van specifieke strategieën, noch wordt gezegd dat ze verschillende strategieën moeten gebruiken. Het traditionele “lenen” algoritme is een strategie gebaseerd op plaatswaarde, dus het is hier opgenomen in 2.NBT.5.

   2.NBT.9
   Leg uit waarom optel- en aftrekstrategieën werken, met behulp van de plaatswaarde en de eigenschappen van bewerkingen. Uitleg kan worden ondersteund door tekeningen of objecten.

   Er staat “kan worden ondersteund door tekeningen”, maar het dwingt u niet om dat te doen, noch beperkt het u tot het gebruik van een specifiek visueel model of type tekening.

   3.OA.3
   Vermenigvuldiging en deling binnen 100 gebruiken om woordproblemen op te lossen in situaties met gelijke groepen, reeksen en meetgrootheden, bijvoorbeeld door gebruik te maken van tekeningen en vergelijkingen met een symbool voor het onbekende getal om het probleem weer te geven.

   De leerling hoeft geen tekening te gebruiken. Dat wordt alleen als mogelijkheid genoemd.

   4.NBT.5
   Een geheel getal van maximaal vier cijfers vermenigvuldigen met een geheel getal van één cijfer, en twee getallen van twee cijfers vermenigvuldigen, met behulp van strategieën die zijn gebaseerd op de plaatswaarde en de eigenschappen van bewerkingen. Illustreer en verklaar de berekening met behulp van vergelijkingen, rechthoekige matrices, en/of areamodellen.

   Let op het “en/of”. Illustreer de berekening, maar het is voldoende om het met vergelijkingen te illustreren.

   Dit gezegd hebbende, vermelden sommige normen wel een specifiek visueel model, zoals een getallenlijn of een rechthoekig oppervlaktemodel, maar dat is minder gebruikelijk dan het geven van een keuze zoals in de normen hierboven.

Conceptuele wiskunde

Er zijn enkele normen die ingaan op de conceptuele kant van wiskunde die basisschoolleerkrachten misschien niet begrijpen als hen niet wordt geleerd wat ze betekenen; bijvoorbeeld:

5. NF.7b
Deling van een geheel getal door een breuk van een eenheid interpreteren, en dergelijke quotiënten berekenen. Bijvoorbeeld, een verhaalcontext maken voor 4 ÷ (1/5), en een visueel breukmodel gebruiken om het quotiënt te tonen. Gebruik het verband tussen vermenigvuldigen en delen om uit te leggen dat 4 ÷ (1/5) = 20 omdat 20 × (1/5) = 4.

Een dergelijk verhaalprobleem zou kunnen zijn: hoeveel stukken van 1/5 voet lang kun je uit een stuk materiaal van 4 voet knippen? Een visueel model kan 4 gehelen laten zien, verdeeld in vijfden. We kunnen dan tellen dat 4 gehelen in totaal 20 kwinten hebben.

5.NF.4b
Vind de oppervlakte van een rechthoek met fractionele zijlengtes door hem te betegelen met vierkanten van de juiste zijlengtes, en laat zien dat de oppervlakte hetzelfde is als zou worden gevonden door de zijlengtes met elkaar te vermenigvuldigen. Vermenigvuldig fractionele zijlengtes om oppervlakten van rechthoeken te vinden, en geef fractionele producten weer als rechthoekige oppervlakten.

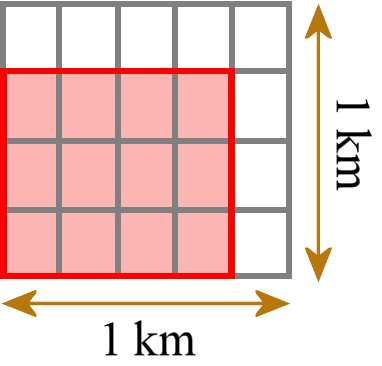Dit betekent bijvoorbeeld een rechthoek met zijlengtes 3/4 km en 4/5 km. Dan betegelen we die met kleine eenheidsrechthoekjes (geen eenheidsvierkantjes; hier gebruikt de norm zelf de verkeerde terminologie) die elk een zijde hebben van 1/4 km en 1/5 km.

We kunnen tellen hoeveel tegeltjes we nodig hebben. We hebben 12 van zulke tegeltjes nodig. Elke tegel heeft een oppervlakte van 1/20 km2, dus de totale oppervlakte is 12/20 km2. Dan controleren we en vergelijken we dat we hetzelfde antwoord krijgen als wanneer we de twee zijlengtes hadden vermenigvuldigd met gewone breukvermenigvuldiging (3/4 km × 4/5 km = 12/20 km2).

Ik heb dit soort problemen altijd in mijn boeken gehad – zelfs voordat CCS kwam.

Sommigen beweren dat kinderen dit conceptuele begrip niet nodig hebben of dat het te moeilijk is. Persoonlijk ben ik het daar niet mee eens. Ik heb er altijd naar gestreefd (ook vóór de CCS) om de concepten van het breukrekenen uit te leggen, zodat leerlingen niet “blindelings de regels volgen” en alleen met breuken kunnen rekenen als ze toevallig de regel goed onthouden. Ik heb altijd de nadruk gelegd op het conceptuele begrip in de wiskunde (zoals mijn lezers weten!).

Maar, ik hoop dat u kunt zien hoe sommige van deze dingen onbekend kunnen zijn voor leraren op school en ouders, en daarom is het geen wonder dat het volgen van Common Core Standards moeilijk voor hen is.

Het is mijn hoop dat Math Mammoth Light Blue Series en de eenheden die ik verkoop op mijn Teachers Pay Teachers en Teachers ‘Notebook winkels kunnen helpen die leraren & ouders die Common Core afgestemd materiaal nodig hebben. En zoals ik al zei, de rest van u kunt vertrouwen in het gebruik ervan ook. Ze bevatten geen “vreemde” of onzinnige wiskunde, maar zijn, zoals altijd, gewoon gebaseerd op de solide basis van het onderwijzen van de concepten van wiskunde samen met de procedures.

Door Maria Miller