Eigenwaarden zijn een speciale verzameling van scalaren geassocieerd met een lineair stelsel van vergelijkingen (i.e., een matrixvergelijking) die soms ook karakteristieke wortels, karakteristieke waarden (Hoffman en Kunze 1971), eigenwaarden of latente wortels worden genoemd (Marcus en Minc 1988, p. 144).

De bepaling van de eigenwaarden en eigenvectoren van een systeem is uiterst belangrijk in de natuurkunde en techniek, waar het equivalent is aan matrixdiagonalisering en voorkomt in veelvoorkomende toepassingen zoals stabiliteitsanalyse, de fysica van roterende lichamen, en kleine oscillaties van trillende systemen, om er maar een paar te noemen. Elke eigenwaarde wordt gekoppeld aan een overeenkomstige zogenaamde eigenvector (of, in het algemeen, een overeenkomstige rechter eigenvector en een overeenkomstige linker eigenvector; er is geen analoog onderscheid tussen links en rechts voor eigenwaarden).

De ontbinding van een vierkante matrix in eigenwaarden en eigenvectoren staat in dit werk bekend als eigendecompositie, en het feit dat deze ontbinding altijd mogelijk is zolang de matrix bestaande uit de eigenvectoren van vierkant is, staat bekend als het eigendecompositietheorema.

Het Lanczos-algoritme is een algoritme voor het berekenen van de eigenwaarden en eigenvectoren voor grote symmetrische schaarse matrices.

Laat een lineaire transformatie zijn, voorgesteld door een matrix . Als er een vector is zodanig dat

(1)

voor een of andere scalair , dan heet de eigenwaarde van met bijbehorende (rechter) eigenvector .

Zodra een vierkante matrix

(2)

is met eigenwaarde , dan voldoen de corresponderende eigenvectoren aan

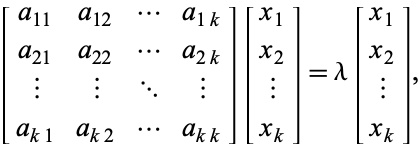(3)

hetgeen equivalent is aan het homogene stelsel

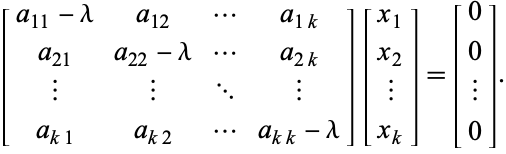(4)

Vergelijking (4) kan compact worden geschreven als

(5)

waar de identieke matrix is. Zoals uit de regel van Cramer blijkt, heeft een lineair stelsel vergelijkingen niet-triviale oplossingen als de determinant verdwijnt, De oplossingen van vergelijking (5) worden dus gegeven door

(6)

Deze vergelijking staat bekend als de karakteristieke vergelijking van , en het linkerlid staat bekend als de karakteristieke polynoom.

Bij voorbeeld, voor een matrix, zijn de eigenwaarden

(7)

die ontstaan als de oplossingen van de karakteristicequatie

(8)

Als alle eigenwaarden verschillend zijn, dan geeft dit onafhankelijke vergelijkingen voor de componenten van elke corresponderende eigenvector, en het systeem wordt niet-degeneraat genoemd. Als de eigenwaarden -voudig ontaard zijn, dan is het systeem ontaard en zijn de eigenvectoren niet lineair onafhankelijk. In dergelijke gevallen kan de extra beperking dat de eigenvectoren orthogonaal moeten zijn,

(9)

waar de Kronecker delta is, worden toegepast om extra beperkingen op te leveren, waardoor een oplossing voor de eigenvectoren mogelijk wordt.

Eigenwaarden kunnen in de Wolfram-taal worden berekend met Eigenwaarden. Eigenvectoren en eigenwaarden kunnen samen worden teruggegeven met het commando Eigensysteem.

Veronderstel dat we de eigenwaarde weten voor

(10)

Toevoeging van een constante maal de identiteitsmatrix aan ,

(11)

dus de nieuwe eigenwaarden zijn gelijk aan de oude plus . Vermenigvuldig met een constante

(12)

de nieuwe eigenwaarden zijn dus de oude vermenigvuldigd met .

Overweeg nu een gelijkvormigheidstransformatie van . Stel is de determinant van , dan

			(13)
			(14)
			(15)

dus de eigenwaarden zijn dezelfde als voor .