In de tip van de maand november 2011 (TOTM) presenteerden we de compressorberekeningen van een casestudy. We hebben de resultaten van de rigoureuze methode vergeleken met de waarden van de snelkoppelingsmethoden. De rigoureuze methode was gebaseerd op een toestandsvergelijking zoals de Soave-Redlich-Kwong (SRK) voor het berekenen van de vereiste enthalpie’s en entropie’s. De enthalpie en entropie worden gebruikt om het vereiste vermogen en de ontladingstemperaturen te bepalen. De resultaten gaven aan dat de nauwkeurigheid van de snelkoppelingsmethode gevoelig is voor de waarde van de ideale gasstaat-warmtecapaciteitsverhouding, k.
Vanuit het oogpunt van de berekening alleen, is de vermogensberekening bijzonder gevoelig voor de specificatie van de massastroom, de zuigtemperatuur en -druk, en de uitlaattemperatuur en -druk. Een compressor zal werken bij wisselende waarden van de variabelen die van invloed zijn op zijn prestaties. Het moeilijkste deel van een compressorberekening is dus de specificatie van een redelijk bereik voor elke variabele en niet de berekening zelf. Referentie benadrukt dat het gebruik van een enkele waarde voor elke variabele niet de juiste manier is om een compressiesysteem te evalueren.
Normaal worden de thermodynamische berekeningen uitgevoerd voor een ideaal (omkeerbaar) proces. De resultaten van een omkeerbaar proces worden vervolgens aangepast aan de werkelijke wereld door het gebruik van een thermodynamisch rendement. In het compressieproces zijn er drie ideale processen die kunnen worden gevisualiseerd: 1) een isotherm proces (PV1=C1), 2) een isentropisch proces (PVk=C2) en 3) een polytropisch proces (PVn=C3). Elk van deze processen kan geschikt worden gebruikt als basis voor het evalueren van de compressiebehoeften, hetzij met de hand, hetzij met de computer. Het isothermische proces wordt echter zelden als basis gebruikt omdat het normale industriële compressieproces niet eens bij benadering bij constante temperatuur wordt uitgevoerd.
Merk op dat Dresser Rand vrij veel werk verricht op het gebied van “bijna constante temperatuur” compressie, met name voor CO2 compressie uit ontluchtingsschoorstenen. Voor details zie:
In deze TOTM laten we zien hoe het rendement van een compressor kan worden bepaald aan de hand van het gemeten debiet, de samenstelling, de aanzuig- en uitblaastemperaturen en -drukken. Een rigoureuze berekening op basis van een toestandsvergelijking en een verkorte methode komen aan de orde en de resultaten worden vergeleken.
Compressorrendement
Compressorrendementen variëren met compressortype, -grootte en -doorzet. Zij kunnen (achteraf) alleen worden bepaald door een compressortest, hoewel compressorfabrikanten meestal goede schattingen kunnen geven. Voor planningsdoeleinden wordt verwezen naar de volgende waarden voor de totale rendementen:
Tabel 1. Totale compressorefficiëntie
|
Compressortype |
Efficiëntie, η |
|
Centrifugaal |
0.70 – 0.85 |
|
Hogesnelheidsreciprocerende |
0.72 – 0.85 |
|
Lagesnelheidsreciprocerende |
0.72 – 0.85 |
|
0.75 – 0.90 |
|
|
.75 – 0,90 |
|
|
Roterende schroef |
0,65 – 0,75 |
Referentie geeft aan dat deze totale efficiënten de gaswrijving binnen de compressor, de mechanische verliezen (lagers, afdichtingen, tandwielkast, enz.) en de tandwielkastverliezen omvatten. De mechanische efficiëntie varieert met de grootte en het type van de compressor, maar 95% is een bruikbaar planningsgetal. Bij de berekening van de opvoerhoogte en de afvoertemperatuur van de compressor wordt een isentropische of polytropische efficiëntie gebruikt (isentropische efficiëntie wordt soms ook adiabatische efficiëntie genoemd). Als 3-4 % efficiëntie (mechanische verliezen) bij de totale efficiëntie in tabel 1 wordt opgeteld, krijgt men over het algemeen een goede schatting van de thermodynamische efficiëntie.
Om de prestaties van een bestaande compressor te evalueren, is het de bedoeling de compressorefficiëntie (η) en het vereiste vermogen te berekenen.
Bekende en gemeten eigenschappen zijn:
a. Gasvolumestroom in standaardtoestand (qS) of gasmassastroom ()
b. Gassamenstelling (zi)
c. Aanzuigdruk (P1) en temperatuur (T1)
d. Afvoerdruk (P2) en temperatuur (T2)
Rendement schatten – strenge methode
Het hart van elke commerciële processtroomsimulatiesoftware is een toestandsvergelijking. Wegens hun eenvoud en relatieve nauwkeurigheid wordt een kubische EOS zoals Soave Redlich-Kwong (SRK) of Peng-Robinson gebruikt. Deze vergelijkingen worden gebruikt voor de berekening van damp-vloeistof-equilibrieën (VLE), enthalpie (h) en entropie (s). Met de juiste binaire interactiecoëfficiënten zijn de proces-simulatieresultaten van deze twee vergelijkingen praktisch gelijk. Daarom wordt in dit werk alleen de SRK gebruikt.
Het isentropisch rendement wordt gedefinieerd door
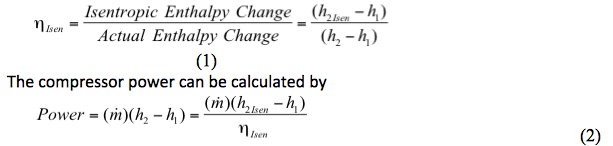
Waar:
ηIsen = Isentropisch rendement
h1 = Zuigenthalpie berekend bij P1, T1, en samenstelling (zi)
h2 = Lossingsenthalpie berekend bij P2, T2, en samenstelling (zi)
h2Isen = Isentrope uitstroomenthalpie bij P2 (of T2), S2Isen =S1, en samenstelling (zi)
![]() = Massadebiet
= Massadebiet
De berekening van het rendement of vermogen van de compressor geschiedt in twee stappen
1. Bepaling van de ideale of isentropische (omkeerbare en adiabatische) enthalpieverandering (h2Isen-h1) van het compressieproces.
2. Bepaling van de werkelijke enthalpieverandering (h2-h1).
De stapsgewijze berekening op basis van een EOS:
a. Ga uit van een stationaire toestand, d.w.z.
b. Veronderstel dat de samenstelling van de toevoer ongewijzigd blijft
c. Bereken zuigenthalpie h1=f(P1, T1, en zi) en entropie s1=f(P1, T1, en zi) door EOS
d. Ga uit van een isentropisch proces en stel s2Isen = f (P2, T2Isen, zi) = s1 = f (P1, T1, zi).
e. Bereken de ideale enthalpie (h2Isen) bij ontladingstoestand voor bekende zi, T2 (of P2) en s2Isen.
f. Bereken de werkelijke enthalpie (h2) bij afblaastoestand voor bekende zi, T2 en P2.
g. Bereken het isentropisch rendement met behulp van vergelijking 1: µIsen = (h2Isen – h1)/(h2 – h1)
h. Bereken het vermogen met behulp van vergelijking 2: ![]()
Rendement schatten – snelkoppelingsmethode
De isentropische pad-exponent (k) of ideale gaswarmtecapaciteitsverhouding (k=CP/CV) kan worden berekend met behulp van de correlatie die in de TOTM van mei 2013 is gepresenteerd:
![]()
Waar:
T = Temperatuur, K (°R)
![]() = Relatieve dichtheid van het gas; verhouding tussen het moleculair gewicht van het gas en het moleculair gewicht van de lucht
= Relatieve dichtheid van het gas; verhouding tussen het moleculair gewicht van het gas en het moleculair gewicht van de lucht
A = 0.000272 (0.000151)
De werkelijke ontladingstemperatuur op basis van een isentropisch pad kan worden geschat door

Oplossen voor het isentropisch rendement,
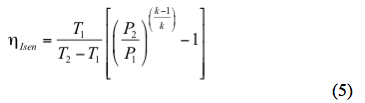
Zo ook, kan de werkelijke ontladingstemperatuur op basis van een polytropisch pad worden geschat door

Oplossen van bovenstaande vergelijking voor de polytropische padcoëfficiënt (n):

Op dezelfde manier kan de werkelijke ontladingstemperatuur op basis van een polytropisch pad worden geschat (ηPoly) door:

De isentropische opvoerhoogte wordt berekend door
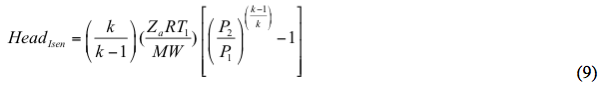
Zo ook, de polytropische opvoerhoogte wordt berekend door
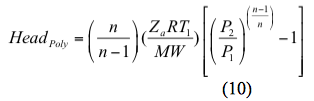
Voor een isentropisch (omkeerbaar en adiabatisch) proces wordt het vermogen berekend door
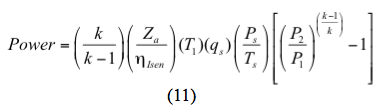
Of voor een polytropisch proces wordt het vermogen berekend door
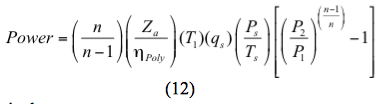
Alternatief:
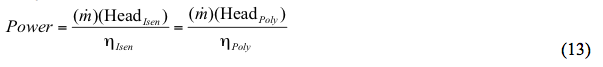
Waar:
Head = Opvoerhoogte van de compressor, m (ft)
Power = Vermogen van de compressor, kW (HP)
R = Universele gasconstante, 848 kg-m/(kmol-K) of (1545 ft-lbf/(lbmol-°R))
PS = Druk in standaardtoestand, kPa (psia)
P1 = zuigdruk, kPa (psia)
P2 = uittreeddruk, kPa (psia)
TS = standaardtemperatuur, K (°R)
T1 = zuigtemperatuur, K (°R)
T2 = uittreedtemperatuur, K (°R)
qS = Gasvolumetrisch debiet bij de standaardtoestand, Sm3/d (scf/dag)
Za = Gemiddelde samendrukbaarheidsfactor van het gas = (Z1+Z2)/2
Z1 = Samendrukbaarheidsfactor van het gas bij zuigtoestand
Z2 = Samendrukbaarheidsfactor van het gas bij afblaastoestand
MW = Molecuulgewicht van het gas
De vermogensberekening moet per compressietrap worden uitgevoerd en vervolgens worden opgeteld voor alle trappen die op één aandrijfeenheid zijn aangesloten.
De stapsgewijze berekening voor de snelkoppelingsmethode
a. Bereken de isentropische exponent (k) met behulp van vergelijking 3 en gebruik daarbij de gemiddelde temperatuur gedefinieerd door T = (T1+3T2)/4. Deze vorm van gemiddelde temperatuur werd gedefinieerd om een betere overeenkomst te verkrijgen tussen de resultaten van de strikte methode en die van de snelkoppelingsmethode.
b. Bereken het isentropisch rendement (ηIsen) met behulp van vergelijking 5.
c. Bereken de polytropische coëfficiënt (n) met behulp van vergelijking 7.
d. Bereken het polytropisch rendement (ηPoly) met behulp van vergelijking 8.
e. Bereken de isentropische en polytropische opvoerhoogte met behulp van respectievelijk vergelijking 9 en vergelijking 10.
f. Bereken het vereiste vermogen per trap met behulp van vergelijking 11 of 12.
Gevalstudie
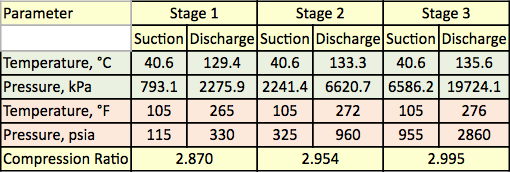
Een aardgasmengsel wordt gecomprimeerd met behulp van een drietraps centrifugaalcompressor. Het stroomdiagram van het proces is weergegeven in figuur 1. Voor elke trap zijn de gemeten druk en temperatuur opgenomen in tabel 1. De gemeten samenstelling van de toevoer, de stroomsnelheden en het berekende molecuulgewicht en de relatieve dichtheid zijn vermeld in tabel 2.
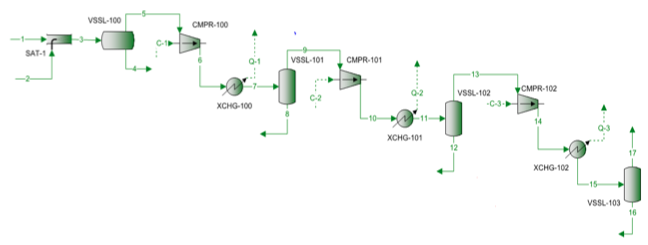
Figuur 1. Processtroomdiagram voor een drietrapscompressie
Tabel 1. Gemeten temperatuur en druk voor de drie compressiefasen
Tabel 2. Gasanalyse en debiet voor de drie compressietrappen
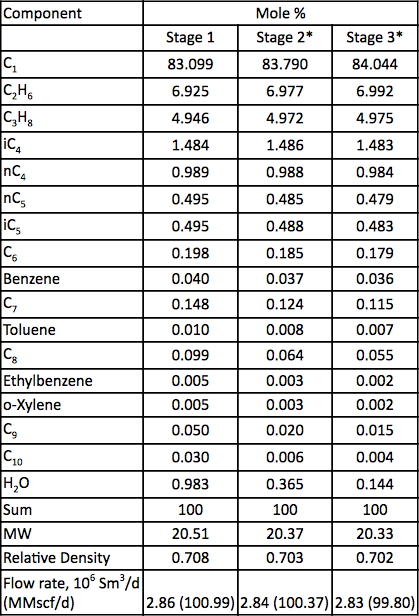
* Berekend
Resultaten en besprekingen
Het in figuur 1 getoonde processtroomdiagram werd gesimuleerd door ProMax software om de rigoureuze berekeningen uit te voeren met behulp van de SRK EOS. Het programma berekende polytropische en isentropische rendementen, opvoerhoogten en compressievermogen. Het programma berekende ook de isentropische pad-exponent (k) en de polytropische pad-exponent (n). Deze berekende resultaten zijn weergegeven in tabel 2 voor alle drie fasen onder SRK-koers. De door ProMax uitgevoerde berekeningen lijken sterk op de stapsgewijze berekeningen van a tot en met h die in de rigoureuze paragraaf zijn beschreven. Tabel 2 bevat ook de resultaten van de snelkoppelingsberekeningen voor de overeenkomstige waarden onder de snelkoppelingsrubriek. De snelkoppelingsberekeningen zijn gebaseerd op de stapsgewijze berekening van a tot en met f die in de paragraaf over de snelkoppelingsmethode is beschreven. De foutenpercentages tussen de rigoureuze methode en de verkorte methoden voor elke fase worden eveneens in tabel 2 gegeven. Tabel 2 geeft aan dat voor de fasen 1 en 2 uitstekende overeenkomsten worden verkregen. Er worden echter grotere afwijkingen geconstateerd voor de isetropische en polytropische exponenten van fase 3 als gevolg van de werking bij hoge druk, die te ver afweek van de ideale omstandigheden voor de gastoestand.
Tabel 3.
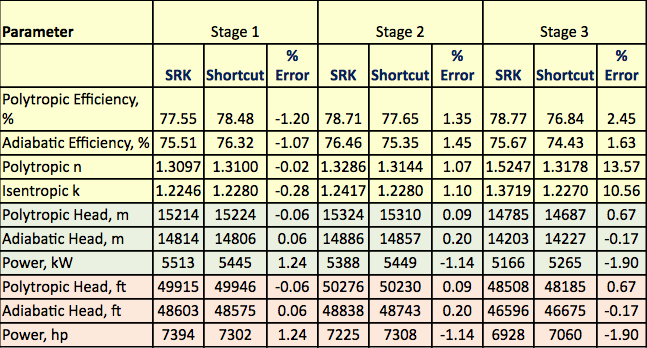
Conclusies
Tabel 2 geeft aan dat er goede overeenkomsten zijn tussen de resultaten van de korte methode en die van de rigoureuze methode. De verschillen tussen de resultaten van de rigoureuze methode en die van de verkorte methode voor faciliteitenberekeningen en planningsdoeleinden zijn verwaarloosbaar. Voor fase 3 wordt, als gevolg van de hogedrukwerking en het te ver afwijken van de ideale gastoestand, een grotere fout waargenomen voor de isentropische exponent (k).
De berekende isentropische exponent (k) in de ProMax is niet de verhouding van de ideale gastoestand-warmtecapaciteit (CP/CV). Het is de waarde van de isentropische exponent die nodig is om een isentropisch pad van inlaat naar uitlaat te verkrijgen. De waarde wordt berekend als een integratie van dat pad. Het is dus een soort “gemiddelde” waarde die het werkelijke isentropische pad weergeeft. Voor ideale gassen zou de waarde gelijk zijn aan de (CP/CV) ratio.
Deze fout in “k” illustreert ook hoe belangrijk het is te specificeren welke correlatie moet worden gebruikt bij het bestellen van een prestatietest (d.w.z., raadpleeg ASME PTC-10 voor meer details), zodat klant en leverancier op dezelfde golflengte zitten wat betreft molecuulgewicht (MW) en k voor de testvloeistof. Voor meer details zie referentie en augustus en september 2010 TOTMs .
Het kan ook de moeite waard zijn op te merken dat bij het trending ‘n’ en de polytropische efficiëntie om de machine conditie te evalueren, de relatieve nauwkeurigheid van meetinstrumenten / apparatuur (temperatuur en druk transducers) en mapping van de compressor prestaties aan de oorspronkelijke prestatiecurve (werkelijke gasvolumestroom versus snelheid), introduceert veel potentiële foutieve bronnen in deze dagelijkse evaluatie.
Merk op dat de nauwkeurigheid van de snelkoppelingsmethoden afhankelijk is van de waarden van k en n. De definitie van gemiddelde temperatuur in de verkorte methode is aangepast om een betere overeenkomst te verkrijgen tussen de isentropische pad-exponent (k) die met de rigoureuze methode is berekend.
Om meer te weten te komen over soortgelijke gevallen en hoe operationele problemen tot een minimum kunnen worden beperkt, raden wij aan onze cursussen G4 (Gas Conditioning and Processing), PF4 (Oil Production and Processing Facilities), ME46 (Compressor Systems-Mechanical Design and Specifications) en ME44 (Fundamentals of Pump and Compressors Systems), te volgen.
PetroSkills biedt consulting-expertise over dit onderwerp en vele andere. Voor meer informatie over deze diensten, bezoek onze website op http://petroskills.com/consulting, of e-mail ons op [email protected].
Dr. Mahmood Moshfeghian
Reference:
3. Soave, G., Chem. Eng. Sci., Vol. 27, pp. 1197-1203, 1972.
4. Peng, D. Y., and Robinson, D. B., Ind. Eng. Chem. Fundam., Vol. 15, p. 59, 1976.
5. ProMax 3.2, Bryan Research and Engineering, Inc, Bryan, Texas, 2014.
6. ASME PTC-10, “Performance test Code on Compressors and Exhausters”, 1997.
7. Honeywell, J. “Belangrijke aspecten van het testen van centrifugale compressoren – deel 1”, tip van de maand, augustus 2010
8. Honeywell, J. “Belangrijke aspecten van het testen van centrifugale compressoren – deel 2”, tip van de maand, september 2010