Stel je een vierkant papier voor dat plat op je bureau ligt. Ik vraag u uw ogen te sluiten. U hoort het papier verschuiven. Als u uw ogen opent, lijkt het papier niet te zijn veranderd. Wat kan ik gedaan hebben terwijl u niet keek?

Het is duidelijk dat ik het papier niet 30 graden gedraaid heb, want dan zou het er anders uitzien.

Ik heb het ook niet omgedraaid over een lijn die bijvoorbeeld een van de hoeken verbindt met het midden van een andere rand. Het papier zou er anders uitzien als ik dat wel had gedaan.

Wat ik echter wel had kunnen doen, was het papier met de klok mee of tegen de klok in draaien over een veelvoud van 90 graden, of het omdraaien over een van de diagonale lijnen of de horizontale en verticale lijnen.

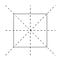
Een handige manier om de transformaties te visualiseren is het markeren van de hoeken van het vierkant.

De laatste optie is dat men niets doet. Dit wordt de identiteitstransformatie genoemd. Samen worden dit allemaal de symmetrietransformaties van het vierkant genoemd.

Ik kan symmetrietransformaties combineren om andere symmetrietransformaties te maken. Bijvoorbeeld, twee omdraaiingen over het lijnstuk BD levert de identiteit op, evenals vier opeenvolgende rotaties van 90 graden tegen de klok in. Een draaiing over de verticale lijn gevolgd door een draaiing over de horizontale lijn heeft het veilige effect als een draaiing van 180 graden. In het algemeen zal elke combinatie van symmetrietransformaties een symmetrietransformatie opleveren. De volgende tabel geeft de regels voor het samenstellen van symmetrietransformaties:

In deze tabel staan R met de subscripts 90, 180 en 270 voor rotaties van 90, 180 en 270 graden tegen de wijzers van de klok in, H voor omklappen over de horizontale lijn, V voor omklappen over de verticale lijn, MD voor omklappen over de diagonaal van linksboven naar rechtsonder, en OD voor omklappen over de andere diagonaal. Om het product van A en B te vinden, ga je naar de rij van A en dan over naar de kolom van B. Bijvoorbeeld, H∘MD=R₉₀.

Er zijn een paar dingen die u kunnen opvallen als u naar de tabel kijkt:

• De operatie ∘ is associatief, wat betekent dat A∘(B∘C) = (A∘B)∘C voor elke transformatie A, B, en C.
• Voor elk paar symmetrietransformaties A en B is de samenstelling A∘B ook een symmetrietransformatie
• Er is een element e zo dat A∘e=e∘A voor elke A
• Voor elke symmetrietransformatie A, is er een unieke symmetrietransformatie A-¹ zo dat A∘A-¹=A-¹∘A=e

We zeggen daarom dat de verzameling symmetrietransformaties van een vierkant, gecombineerd met compositie, een wiskundige structuur vormt die een groep wordt genoemd. Deze groep heet D₄, de dihedraalgroep voor het vierkant. Deze structuren zijn het onderwerp van dit artikel.

Definitie van een groep

Een groep ⟨G,*⟩ is een verzameling G met een regel * voor het combineren van twee elementen in G die voldoet aan de groepsaxioma’s:

In het abstracte schrappen we vaak * en schrijven we a*b als ab en duiden we * aan als vermenigvuldiging.

Het is niet noodzakelijk dat * commutatief is, wat betekent dat a*b=b*a. Je kunt dit zien door naar de tabel van D₄ te kijken, waar H∘MD=R₉₀ maar MD∘H=R₂₇₀. Groepen waarbij * commutatief is worden abeliaanse groepen genoemd naar Neils Abel.

Abeliaanse groepen zijn eerder uitzondering dan regel. Een ander voorbeeld van een niet-abeliaanse groep zijn de symmetrietransformaties van een kubus. Beschouw alleen rotaties om de assen:

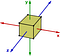
Als ik eerst 90 graden linksom om de y-as draai en dan 90 graden linksom om de z-as dan heeft zijn een ander resultaat dan wanneer ik eerst 90 graden om de z-as draai en dan 90 graden om de y-as.

Het is mogelijk voor een element om zijn eigen inverse te zijn. Beschouw de groep die bestaat uit 0 en 1 met de operatie van binaire optelling. De tabel daarvan is:

Het is duidelijk dat 1 zijn eigen inverse is. Dit is ook een abeliaanse groep. Maak je geen zorgen, de meeste groepen zijn niet zo saai.

Meer voorbeelden van groepen zijn:

• De verzameling gehele getallen met optelling.
• De verzameling rationale getallen zonder 0 met vermenigvuldiging.
• De verzameling oplossingen van de veeltermvergelijking xⁿ-1=0, de n-de wortels van de eenheid genoemd, met vermenigvuldiging.

Hier zijn enkele voorbeelden die geen groepen zijn:

• De verzameling van natuurlijke getallen onder optelling is geen groep omdat er geen inversen zijn, wat de negatieve getallen zouden zijn.
• De verzameling van alle rationale getallen inclusief 0 bij vermenigvuldiging is geen groep omdat er geen rationaal getal q is waarvoor 0/q=1, dus niet elk element heeft een inverse.

Groepsstructuur

Een groep is veel meer dan alleen maar een klodder die aan de vier axioma’s voldoet. Een groep kan een inwendige structuur hebben, en deze structuur kan zeer ingewikkeld zijn. Een van de fundamentele problemen in de abstracte algebra is te bepalen hoe de interne structuur van een groep eruit ziet, omdat in de echte wereld de groepen die werkelijk bestudeerd worden veel groter en ingewikkelder zijn dan de eenvoudige voorbeelden die we hier gegeven hebben.

Een van de basistypen van interne structuur is een ondergroep. Een groep G heeft een ondergroep H als H een deelverzameling van G is en:

• Voor a,b∈H, a*b∈H en b*a∈H
• Voor a∈H, a-¹∈H
• De identiteit is een element van H

Als H≠G dan zegt men dat H een eigenlijke ondergroep is. De ondergroep van G die alleen uit de identiteit bestaat, wordt de triviale ondergroep genoemd.

Een niet-abeliaanse groep kan commutatieve ondergroepen hebben. Beschouw de vierkante dihedrale groep die we in de inleiding hebben besproken. Deze groep is niet abeliaans, maar de subgroep van rotaties is abeliaans en cyclisch:

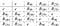
We geven nu twee voorbeelden van groepsstructuur.

Zelfs als een groep G niet abeliaans is, kan het toch zo zijn dat er een verzameling elementen van G is die pendelt met alles in G. Deze verzameling wordt het centrum van G genoemd. Het centrum C is een ondergroep van G. Bewijs:

Stel nu dat f een functie is waarvan domein en bereik beide G zijn. Een periode van f is een element a∈G zo dat f(x)=f(ax) voor alle x∈G. De verzameling P van perioden van f is een ondergroep van G. Bewijs:

Finiete groepen zijn eindig gegenereerd

We zagen dat cyclische groepen door een enkel element worden gegenereerd. Als het mogelijk is om elk element van een groep G te schrijven als producten van een (niet noodzakelijk eigen) deelverzameling A van G dan zeggen we dat A G genereert en schrijven we dit als G=⟨A⟩. Het meest “nou, duh” bewijs dat je ooit zult zien is het bewijs dat alle eindige groepen worden gegenereerd door een eindige voortbrengende verzameling:

• Laat G eindig zijn. Elk element van G is een product van twee andere elementen van G, dus G=⟨G⟩. QED.

We sluiten dit artikel af met een toepassing.

Foutbestendige communicatie

De eenvoudigste manier om digitale informatie over te brengen is deze te coderen in binaire reeksen van vaste lengte. Geen enkel communicatiesysteem is volledig vrij van interferentie, zodat er altijd een kans bestaat dat de verkeerde gegevens worden ontvangen. De methode van de maximale waarschijnlijkheidsdecodering is een eenvoudige en doeltreffende methode om overdrachtsfouten op te sporen en te corrigeren.

Laat 𝔹ⁿ de verzameling binaire reeksen, of woorden, zijn van lengte n. Het is eenvoudig aan te tonen dat 𝔹ⁿ een abeliaanse groep is onder binaire optelling zonder overdracht (zodat bijvoorbeeld 010+011=001). Merk op dat elk element zijn eigen inverse is. Een code C is een deelverzameling van 𝔹ⁿ. Het volgende is een voorbeeld van een code in 𝔹⁶:

C = {000000, 001011, 010110, 011101, 100101, 101110, 110011, 111000}

De elementen van een code worden codewoorden genoemd. Alleen codewoorden worden verzonden. Er is sprake van een fout wanneer interferentie een bit in een verzonden woord verandert. De afstand d(a,b) tussen twee codewoorden a en b is het aantal cijfers waarin twee codewoorden verschillen. De minimum afstand van een code is de kleinste afstand tussen twee van zijn codewoorden. Voor de voorbeeldcode hierboven is de minimumafstand drie.

In de methode van de maximale waarschijnlijkheid decodering moet, indien we een woord x ontvangen, dat fouten kan bevatten, de ontvanger x interpreteren als het codewoord a zodanig dat d(a,x) een minimum is. Ik zal aantonen dat voor een code van minimale afstand m dit altijd (1) fouten kan detecteren die minder dan m bits veranderen en (2) fouten kan corrigeren die ½(m-1) of minder bits veranderen.

In onze voorbeeldcode is m=3 en de bol met straal ½(m-1)=1 om het codewoord 011101 is {011101, 111101, 001101, 011001, 010101, 011111, 011100}. Dus als de ontvanger een van deze woorden ontvangt, weet hij dat hij 011101 had moeten ontvangen.

Dat is allemaal goed en wel, maar wat heeft dit alles met groepentheorie te maken? Het antwoord ligt in de manier waarop we de codes produceren waarmee deze methode werkt.

Het is mogelijk dat een code in 𝔹ⁿ een subgroep vormt. In dat geval zeggen we dat de code een groepscode is. Groepscodes zijn eindige groepen en worden dus eindig gegenereerd. We zullen zien hoe we een code kunnen produceren door een genererende set te vinden.

Een code kan zo worden gespecificeerd dat de eerste paar bits van elk codewoord de informatiebits worden genoemd en de bits aan het eind de pariteitsbits. In onze voorbeeldcode C zijn de eerste drie bits informatiebits en de laatste drie pariteitsbits. De pariteitsbits voldoen aan pariteitscontrolevergelijkingen. Voor een codewoord A₁A₂A₃A₄A₅A₆ zijn de pariteitsvergelijkingen A₄=A₁+A₂, A₅=A₂+A₃, en A₆=A₁+A₃. Pariteitsvergelijkingen bieden nog een laag bescherming tegen fouten: als aan een van de pariteitsvergelijkingen niet wordt voldaan, is er een fout opgetreden.

Hier volgt wat we doen. Stel dat we codewoorden willen met m informatiebits en n pariteitsbits. Om een groepscode te genereren, schrijven we een matrix met m rijen en m+n kolommen. In het blok gevormd door de eerste m kolommen, schrijven we de m×m identiteitsmatrix. In kolom j voor m+1≤j≤m_n, schrijf een 1 in de k-de rij indien Aₖ voorkomt in de pariteitsvergelijking voor pariteitsbit Aⱼ en 0 anders. In onze voorbeeldcode is de matrix:

Zulk een matrix wordt een genererende matrix voor de groepscode genoemd. Men kan rechtstreeks nagaan dat de rijen C voortbrengen:

De rijen van een willekeurige voortbrengende matrix vormen een voortbrengende set voor een groepscode C. Bewijs:

• Identiteit en inverses: Elke rij bij zichzelf opgeteld geeft de identiteit, een reeks bestaande uit alle nullen.
• Sluiting: Als A,B∈C dan zijn A en B sommen van rijen van de voortbrengende matrix dus A+B is ook een som van rijen van de voortbrengende matrix. Dus A+B∈C.

Dit laat ons toe een code te genereren, nu zal ik tonen hoe we een nuttige code kunnen genereren.

Definieer het gewicht w(x) als het aantal enen in x. Bijvoorbeeld, w(100101)=3. Het is duidelijk dat w(x)=d(x,0) waarbij 0 een woord is waarvan de cijfers allemaal nullen zijn. Het minimum gewicht W van een code is het gewicht van het niet-nul codewoord met de minste enen in de code. Voor een code van minimum afstand m, d(x,0)≥m dus w(x)≥m en dus W=m.

Ontdek dat een woord, om als codewoord beschouwd te worden, moet voldoen aan een reeks pariteitscontrolevergelijkingen. Voor onze voorbeeldcode zijn dat A₄=A₁+A₂, A₅=A₂+A₃, en A₆=A₁+A₃. We kunnen deze ook schrijven als een lineair stelsel:

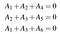
Wat zelf geschreven kan worden in termen van dotproducten:

Of in compactere vorm als Ha=0 waarbij a=(A₁,A₂,A₃,A₄,A₅,A₆) en H de pariteitscontrolematrix voor de code is:

Met directe berekeningen kan men nagaan dat als w(a)≤2 er geen Ha=0 kan zijn. In het algemeen is het minimumgewicht t+1, waarbij t het kleinste getal is dat een verzameling van t kolommen van H niet bij elkaar optelt tot nul (d.w.z. dat ze lineair onafhankelijk zijn). Dit bewijzen zou ons net iets te ver in de lineaire algebra brengen.

Als dat je afschrikt, maak je dan geen zorgen. We kunnen een aantal zeer goede codes maken zonder dat door gebruik te maken van het feit dat het resultaat dat ik zojuist noemde impliceert dat als elke kolom van H niet nul is en geen twee kolommen gelijk zijn, het minimum gewicht, en dus de minimum afstand van de code, ten minste drie is. Dit is zeer goed: als ons communicatiesysteem naar verwachting één bitfout zal hebben voor elke honderd verzonden woorden, dan zal slechts één op de tienduizend verzonden woorden een ongecorrigeerde fout hebben en één op de miljoen verzonden woorden zal een onopgemerkte fout hebben.

Dus nu hebben we een recept voor het maken van een bruikbare code voor het maximale-waarschijnlijkheidsdetectieschema voor codewoorden die m informatiebits en n pariteitsbits bevatten:

• Maak een matrix met m+n kolommen en n rijen. Vul de matrix met enen en nullen zodat geen twee kolommen hetzelfde zijn en geen enkele kolom alleen maar nullen bevat.
• Elke rij van de resulterende pariteitscontrolematrix komt overeen met één van de pariteitsbitvergelijkingen. Schrijf ze als een stelsel vergelijkingen en los ze zo op dat elk pariteitsbit wordt geschreven in termen van de informatiebits.
• Maak een matrix met m+n kolommen en m rijen. Schrijf in het blok gevormd door de eerste m kolommen de m×m identiteitsmatrix. Schrijf in kolom j voor m+1≤j≤m_n, een 1 in de k-de rij als Aₖ voorkomt in de pariteitsvergelijking voor pariteitsbit Aⱼ en 0 anders.
• De rijen van deze matrix zijn de generatoren van een codegroep met een minimale afstand van ten minste drie. Dit is de code die we zullen gebruiken.

Als voorbeeld, stel dat ik een eenvoudige, acht-woord code nodig heb en ik heb alleen wat basis foutdetectie nodig en geen correctie, dus ik kan wegkomen met een minimale afstand van twee. Ik wil drie informatiebits en twee pariteitsbits. Ik schrijf de volgende pariteitscontrolematrix op:

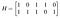
Er zijn twee paren kolommen die gelijk zijn, dus de kleinste t waarvoor een verzameling van t kolommen lineair onafhankelijk is, is één, dus het minimale gewicht, en dus de minimale afstand die ik zal hebben, is twee. De rijen stellen de pariteitsvergelijkingen A₄=A₁+A₃ en A₅=A₁+A₂+A₃ voor. Mijn generatiematrix is dus:

En de rijen van deze matrix genereren de codegroep:

• {00000, 00111, 01001, 01110, 10011, 10100, 111010, 11101}

Slotopmerkingen

Abstracte algebra is een diepgaand onderwerp met verstrekkende implicaties, maar het is ook heel gemakkelijk te leren. Afgezien van een paar passages over lineaire algebra, is bijna alles wat ik hier besproken heb toegankelijk voor iemand die alleen algebra op de middelbare school heeft gehad.

Toen ik voor het eerst op het idee kwam om dit artikel te schrijven, wilde ik het eigenlijk over de Rubiks kubus hebben, maar uiteindelijk wilde ik een voorbeeld kiezen dat alleen met de meest elementaire ideeën uit de groepentheorie kon worden behandeld. Bovendien is er zoveel te vertellen over de Rubik’s kubus groep dat het een zelfstandig stuk verdient, dus dat komt binnenkort.

Mijn college cursussen in abstracte algebra waren gebaseerd op het boek A Book of Abstract Algebra van Charles Pinter, dat een toegankelijke behandeling is. De voorbeelden in dit artikel zijn allemaal met enige aanpassing ontleend aan Pinter.

Als laatste opmerking, alle afbeeldingen die niet worden genoemd zijn mijn eigen originele werk en mogen worden gebruikt met bronvermelding. Zoals altijd stel ik correcties of verzoeken om verduidelijking op prijs.