Zoals de P-Only regelaar berekent het Proportional-Integral (PI) algoritme een regeluitgangssignaal (CO) en zendt dit iedere sample tijd, T, naar het uiteindelijke regelelement (b.v. klep, variabele snelheidspomp). De berekende CO van het PI-algoritme wordt beïnvloed door de regelaarafstellingsparameters en de regelaarfout, e(t).
PI-regelaars hebben twee afstellingsparameters die moeten worden aangepast. Hoewel dit de afstemming moeilijker maakt dan een P-only regelaar, zijn ze niet zo complex als de PID regelaar met drie parameters.
Integrale werking stelt PI regelaars in staat om offset te elimineren, een belangrijk zwak punt van een P-only regelaar. Aldus bieden PI-regelaars een evenwicht tussen complexiteit en mogelijkheden, waardoor zij verreweg het meest gebruikte algoritme in procesbesturingstoepassingen zijn.
Het PI-algoritme
Hoewel verschillende leveranciers wat in wezen hetzelfde algoritme is in verschillende vormen gieten, verkennen we hier wat op verschillende manieren wordt beschreven als de afhankelijke, ideale, continue, positievorm:
![]()
Waar:
CO = uitgangssignaal van de regelaar (de draad eruit)
CObias = bias of nulwaarde van de regelaar; ingesteld door bumpless overdracht zoals hieronder uitgelegd
e(t) = huidige regelaarfout, gedefinieerd als SP – PV
SP = instelpunt
PV = gemeten procesvariabele (de draad in)
Kc = regelaarversterking, een afstemparameter
Ti = resettijd, een afstemparameter
De eerste twee termen rechts van het gelijkheidsteken zijn identiek aan de P-Only regelaar waarnaar boven aan dit artikel wordt verwezen.
De integrale modus van de regelaar is de laatste term van de vergelijking. De functie ervan is de fout van de regelaar, e(t), in de tijd te integreren of voortdurend bij elkaar op te tellen.
Enkele dingen die we moeten weten over de parameter voor de afstelling van de resettijd, Ti:
| ▪ | Hij geeft een afzonderlijk gewicht aan de integrale term, zodat de invloed van de integrale actie onafhankelijk kan worden ingesteld. |
| ▪ | Het staat in de noemer zodat kleinere waarden een groter gewicht geven aan (d.w.z. de invloed van) de integrale term vergroten. |
| ▪ | Het heeft tijdseenheden dus het is altijd positief. |
Functie van de proportionele term
Net als bij de P-Only regelaar voegt de proportionele term van de PI-regelaar, Kc-e(t), toe aan of onttrekt deze van CObias op basis van de grootte van de regelaarfout e(t) op elk tijdstip t.
Als e(t) groeit of krimpt, groeit of krimpt de hoeveelheid die aan CObias wordt toegevoegd onmiddellijk en proportioneel. Het verleden en het huidige traject van de regelaarfout hebben geen invloed op de berekening van de proportionele term.
De onderstaande plot (klik voor een grote weergave) illustreert dit idee voor een set point respons. De fout die in de proportionele berekening wordt gebruikt, wordt in de grafiek weergegeven:
▪ Op tijdstip t = 25 min, e(25) = 60-56 = 4
▪ Op tijdstip t = 40 min, e(40) = 60-62 = -2
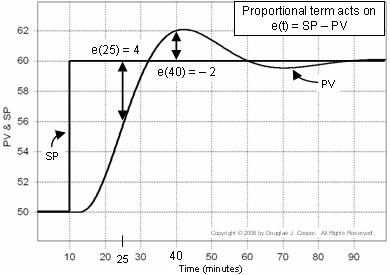
Wanneer we bedenken dat regelfout e(t) = SP – PV, kunnen we, in plaats van PV en SP als afzonderlijke sporen te beschouwen zoals we hierboven doen, e(t) op elk punt in de tijd t berekenen en plotten.
Hieronder (klik voor een grote weergave) zijn de gegevens identiek aan die hierboven, alleen zijn ze herschikt als een plot van e(t) zelf. Merk op dat in de bovenstaande plot PV = SP = 50 voor de eerste 10 minuten, terwijl in de onderstaande foutplot e(t) = 0 voor dezelfde tijdsperiode.
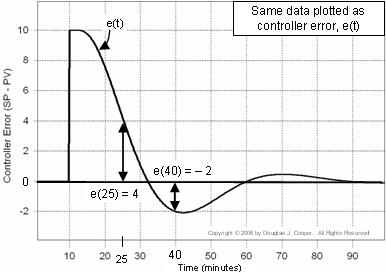
Deze plot is nuttig omdat hij ons helpt te visualiseren hoe de fout van de regelaar voortdurend van grootte en teken verandert naarmate de tijd verstrijkt.
Functie van de integrale term
Waar de proportionele term de huidige grootte van e(t) alleen beschouwt op het moment van de regelaarberekening, beschouwt de integrale term de geschiedenis van de fout, of hoe lang en hoe ver de gemeten procesvariabele in de loop van de tijd van het instelpunt is afgeweken.
Integratie is een voortdurende optelsom. Integratie van de fout in de tijd betekent dat we de volledige foutgeschiedenis van de regelaar tot op het huidige moment optellen, te beginnen bij het moment waarop de regelaar voor het eerst op automatisch is overgeschakeld.
Fout van de regelaar is e(t) = SP – PV. In de onderstaande grafiek (klik voor een grote weergave) wordt de integrale som van de fout berekend als de gearceerde gebieden tussen de SP- en PV-sporen.
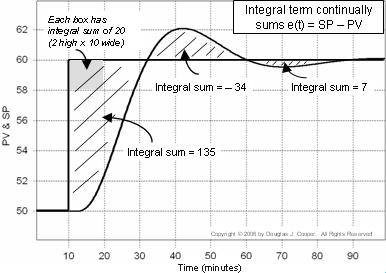
Elk vakje in de grafiek heeft een integrale som van 20 (2 hoog bij 10 breed). Als we het aantal vakjes tellen (inclusief fracties van vakjes) dat zich in de gearceerde gebieden bevindt, kunnen we de integrale som van de fout berekenen.
Dus wanneer de PV rond t = 32 voor het eerst het setpoint overschrijdt, is de integrale som gegroeid tot ongeveer 135. We schrijven de integrale term van de PI-regelaar als:
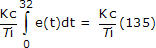
Omdat het de fout van de regelaar is die de berekening stuurt, krijgen we een direct beeld van de situatie aan de hand van een controller error plot, zoals hieronder afgebeeld (klik voor een grote weergave):

Merk op dat de integraal van elk gearceerd gedeelte hetzelfde teken heeft als de fout. Aangezien de integrale som begint te accumuleren wanneer de regelaar voor het eerst in de automatische stand wordt gezet, groeit de totale integrale som zolang e(t) positief is en krimpt deze wanneer deze negatief is.
Op het tijdstip t = 60 min op de plots is de integrale som 135 – 34 = 101. De respons is grotendeels voltooid op t = 90 min, en de integrale som is dan 135 – 34 + 7 = 108.
Integrale actie elimineert offset
De vorige zin maakt een subtiele maar zeer belangrijke opmerking. De respons is grotendeels voltooid op het tijdstip t = 90 min, maar toch is de integrale som van alle fouten niet nul.
In dit voorbeeld heeft de integrale som een eind- of restwaarde van 108. Het is deze restwaarde die de integrale actie van de PI-regelaar in staat stelt om offset te elimineren.
Zoals besproken in een vorig artikel, ervaren de meeste processen onder P-only regeling offset tijdens normaal bedrijf. Offset is een aanhoudende waarde voor regelaarfout (d.w.z. PV is niet gelijk aan SP in steady state).
We herkennen van de P-Only-regelaar:
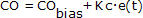
dat CO altijd gelijk zal zijn aan CObias tenzij we er iets aan toevoegen of van aftrekken.
De enige manier waarop we iets hebben om toe te voegen aan of af te trekken van CObias in de bovenstaande P-Only-vergelijking is als e(t) niet nul is. Als e(t) niet constant op nul staat, is PV niet gelijk aan SP en hebben we een offset.
Met de PI-regelaar:
![]()
weten we nu dat de integrale foutensom een eind- of restwaarde kan hebben nadat een reactie is voltooid. Dit is belangrijk omdat dit betekent dat e(t) nul kan zijn, maar dat we toch iets kunnen toevoegen aan of aftrekken van CObias om de uiteindelijke regelaaroutput, CO, te vormen.
Zolang er dus sprake is van een fout (zolang e(t) niet nul is), zal de integrale term in grootte toenemen of afnemen om de CO te beïnvloeden. De veranderingen in CO zullen pas ophouden wanneer PV gedurende een langere periode gelijk is aan SP (wanneer e(t) = 0).
Op dat moment kan de integrale term een restwaarde hebben zoals zojuist besproken. Deze restwaarde van integratie, wanneer toegevoegd aan CObias, creëert in wezen een nieuwe totale biaswaarde die overeenkomt met het nieuwe werkingsniveau.
In feite stelt de integrale actie voortdurend de biaswaarde opnieuw in om de offset te elimineren wanneer het werkingsniveau verandert.
Uitdagingen van PI-regeling
Er zijn uitdagingen bij het gebruik van het PI-algoritme:
| ▪ | De twee afstelparameters werken op elkaar in en hun invloed moet door de ontwerper in evenwicht worden gebracht. |
| ▪ | De integrale term heeft de neiging het oscillerende of rollende gedrag van de procesrespons te versterken. |
Omdat de twee afstemparameters op elkaar inwerken, kan het een uitdaging zijn om tot de “beste” afstemmingswaarden te komen. De waarde en het belang van ons ontwerp- en afstemrecept nemen toe naarmate de regelaar complexer wordt.
Initialiseren van de regelaar voor overdracht zonder hobbels
Wanneer we een regelaar overschakelen van handmatige modus naar automatische (van open lus naar gesloten lus), willen we dat het resultaat niet onbeduidend is. Dat wil zeggen, we willen niet dat de omschakeling abrupte regelacties veroorzaakt die ons proces beïnvloeden of verstoren
We bereiken dit gewenste resultaat bij de omschakeling door de integrale foutensom van de regelaar op nul te initialiseren. Ook worden het instelpunt en de biaswaarde van de regelaar geïnitialiseerd door:
▪ SP gelijk te stellen aan de huidige PV
▪ CObias gelijk te stellen aan de huidige CO
Met de integrale foutensom op nul ingesteld, is er niets toe te voegen aan of af te trekken van CObias dat een plotselinge verandering in de huidige regelaaruitgang zou veroorzaken. Met het setpoint gelijk aan de gemeten procesvariabele, is er geen fout om een verandering in onze CO aan te sturen. En met de regelaar bias ingesteld op onze huidige CO-waarde, zijn we standaard voorbereid om de huidige werking te handhaven.
Dus, wanneer we overschakelen van handmatige naar automatische modus, hebben we “bumpless overdracht” zonder verrassingen. Dit is een resultaat dat iedereen waardeert.
Reset Time Versus Reset Rate
Verschillende leveranciers gieten hun regelalgoritmen in iets andere vormen. Sommigen gebruiken proportionele band in plaats van regelaarversterking. Ook gebruiken sommigen de resetsnelheid, Tr, in plaats van de resettijd. Deze zijn eenvoudigweg het omgekeerde van elkaar:
Tr = 1/Ti
Hoe de afstelparameters ook worden uitgedrukt, de PI-algoritmen zijn allemaal even geschikt.
Het is echter van cruciaal belang uw fabrikant te kennen voordat u begint met het afstellen van uw regelaar, omdat de parameterwaarden moeten worden afgestemd op uw specifieke algoritmevorm.Commerciële software voor regelaarontwerp en -afstemming pakt dit probleem automatisch voor u aan.
Implementeren van een PI-regelaar
We verkennen PI-regelaarontwerp, -afstemming en -implementatie op de warmtewisselaar in dit artikel en de zwaartekracht afgevoerde tanks in dit artikel.