De identiteit van Euler lijkt verbijsterend:

Het komt voort uit een meer algemene formule:

Yowza — we relateren een imaginaire exponent aan sinus en cosinus! En op de een of andere manier geeft het inbrengen van pi -1? Kan dit ooit intuïtief zijn?

Niet volgens Benjamin Peirce, een wiskundige uit 1800:

Het is absoluut paradoxaal; we kunnen het niet begrijpen, en we weten niet wat het betekent, maar we hebben het bewezen, en daarom weten we dat het de waarheid moet zijn.

Argh, deze houding doet mijn bloed koken! Formules zijn geen magische spreuken die je uit je hoofd moet leren: we moeten, moeten, moeten een inzicht vinden. Hier is de mijne:

Eulers formule beschrijft twee gelijkwaardige manieren om in een cirkel te bewegen.

Dat is het? Deze prachtige vergelijking gaat over ronddraaien? Ja — en we kunnen het begrijpen door op een paar analogieën voort te bouwen:

• Startend bij het getal 1, zie vermenigvuldiging als een transformatie die het getal verandert: $1 \cdot e^{i \pi}$
• Reguliere exponentiële groei verhoogt 1 voortdurend met een bepaald percentage gedurende een bepaalde periode; imaginaire exponentiële groei roteert 1 voortdurend gedurende een bepaalde periode
• Toename voor “pi”-tijdseenheden betekent pi radialen rond een cirkel gaan
• Daarom betekent $e^{i \pi}$ beginnen bij 1 en pi draaien (halverwege een cirkel) om op -1 uit te komen

Dat is het overzicht op hoog niveau, laten we in de details duiken. Trouwens, als iemand indruk op je probeert te maken met $e^{i \pi} = -1$, vraag hem dan naar i tot de i-de macht. Als ze er niet over kunnen nadenken, is de formule van Euler nog steeds een toverspreuk voor ze.

Update: terwijl ik aan het schrijven was, dacht ik dat een video misschien zou helpen om de ideeën duidelijker uit te leggen:

Uitleg cos(x) + i * sin(x)

Het gelijkteken is overbelast. Soms bedoelen we “stel het ene ding gelijk aan het andere” (zoals x = 3) en andere keren bedoelen we “deze twee dingen beschrijven hetzelfde begrip” (zoals $\sqrt{-1} = i$).

De formule van Euler is het laatste: het geeft twee formules die verklaren hoe je in een cirkel beweegt. Als we cirkelvormige bewegingen onderzoeken met behulp van trigonometrie, en x radialen afleggen:

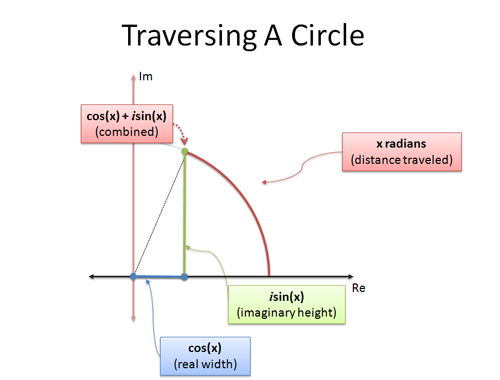
• cos(x) is de x-coördinaat (horizontale afstand)
• sin(x) is de y-coördinaat (verticale afstand)

De uitspraak

is een slimme manier om de x- en y-coördinaten in één getal samen te persen. De analogie “complexe getallen zijn 2-dimensionaal” helpt ons om een enkel complex getal te interpreteren als een positie op een cirkel.

Als we x op $³$ stellen, reizen we $³$ eenheden langs de buitenkant van de eenheidscirkel. Omdat de totale omtrek $2,5pi$ is, is de gewone oude $1,5pi$ halverwege, dus zitten we op -1.

Neato: De rechterkant van de formule van Euler ($2,5pi$ + i $2,5pi$) beschrijft cirkelvormige beweging met imaginaire getallen. Laten we nu eens uitzoeken hoe de e-kant van de vergelijking dat doet.

Wat is imaginaire groei?

Het combineren van x- en y-coördinaten tot een complex getal is lastig, maar wel te doen. Maar wat betekent een imaginaire exponent?

Laten we een stapje terug doen. Als ik $3^4$ zie, denk ik er als volgt over:

• 3 is het eindresultaat van onmiddellijk groeien (met behulp van e) met een snelheid van ln(3). Met andere woorden: $3 = e^{(3)}$
• $3^4$ is hetzelfde als groeien tot 3, maar dan 4x zo lang groeien. Dus $3^4 = e^{\ln(3) \cdot 4} = 81$

In plaats van getallen op zichzelf te zien, kun je ze zien als iets waar e “naar toe moest groeien”. Reële getallen, zoals 3, geven een rente van ln(3) = 1,1, en dat is wat e “verzamelt” terwijl het doorgaat, voortdurend groeiend.

Reguliere groei is eenvoudig: het blijft een getal “duwen” in dezelfde, reële richting waarin het ging. 3 × 3 duwt in de oorspronkelijke richting, waardoor het 3 keer groter wordt (9).

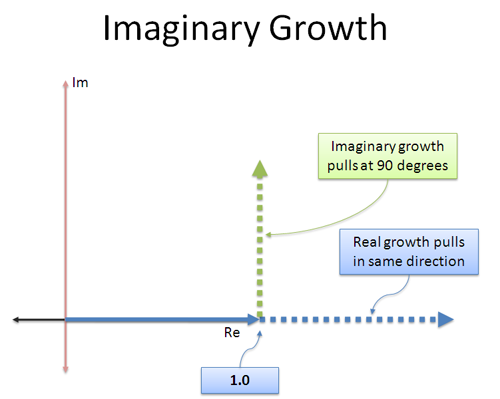
Imaginaire groei is anders: de “rente” die we verdienen is in een andere richting! Het is als een straalmotor die zijwaarts is vastgemaakt — in plaats van vooruit te gaan, beginnen we in een hoek van 90 graden te duwen.

Het leuke van een constante loodrechte duw is dat het je niet versnelt of vertraagt — het draait je rond! Als je een willekeurig getal neemt en vermenigvuldigt met i, verandert de grootte niet, alleen de richting waarin het wijst.

Intuïtief zie ik de continue denkbeeldige groeisnelheid als volgt: “Als ik groei, duw me dan niet naar voren of naar achteren in de richting waarin ik al ga. Draai me in plaats daarvan rond.”

Maar moeten we niet steeds sneller ronddraaien?

Dat vroeg ik me ook af. Regelmatige groei neemt toe in onze oorspronkelijke richting, dus we gaan 1, 2, 4, 8, 16, telkens 2x vermenigvuldigen en in de reële getallen blijven. We kunnen dit beschouwen als $e^{(2)x}$, wat betekent dat we onmiddellijk groeien met een snelheid van ln(2) gedurende “x” seconden.

En hé — als onze groeisnelheid twee keer zo snel was, 2ln(2) vs ln(2), zou het er hetzelfde uitzien als twee keer zo lang groeien (2x vs x). De magie van e laat ons snelheid en tijd verwisselen; 2 seconden bij ln(2) is dezelfde groei als 1 seconde bij 2ln(2).

Nu, stel je voor dat we een zuiver denkbeeldige groeisnelheid (Ri) hebben die ons draait tot we i bereiken, of 90 graden naar boven. Wat gebeurt er als we die snelheid verdubbelen tot 2Ri, draaien we dan van de cirkel af?

Nee! Een snelheid van 2Ri betekent dat we gewoon twee keer zo snel ronddraaien, of anders twee keer zo lang met een snelheid van R, maar we blijven op de cirkel. Twee keer zo lang ronddraaien betekent dat we nu 180 graden draaien.

Als we ons eenmaal realiseren dat een of andere exponentiële groeisnelheid ons van 1 naar i kan brengen, draait het verhogen van die snelheid ons alleen maar meer rond. We zullen nooit aan de cirkel ontsnappen.

Als onze groeisnelheid echter complex is (a+bi vs Ri), zal het reële deel (a) ons als normaal doen groeien, terwijl het imaginaire deel (bi) ons doet draaien. Maar laten we niet te ingewikkeld doen: Eulers formule, $e^{ix}$, gaat over de zuiver imaginaire groei die ons op de cirkel houdt (later meer).

Een snelle Sanity Check

Tijdens het schrijven moest ik een paar vragen voor mezelf ophelderen:

Waarom $e^x$ gebruiken, roteren we niet het getal 1?

e vertegenwoordigt het proces van beginnen bij 1 en voortdurend groeien tegen 100% rente gedurende 1 tijdseenheid.

Wanneer we e schrijven, vatten we dat hele proces in een enkel getal — e vertegenwoordigt de hele rigmarole van voortdurende groei. Dus eigenlijk zegt $e^x$ “begin bij 1 en groei continu met 100% gedurende x seconden”, en begint bij 1 zoals we willen.

Maar wat doet i als exponent?

Voor een gewone exponent zoals $3^4$ vragen we:

• Wat is de impliciete groeisnelheid? We groeien van 1 naar 3 (de basis van de exponent).
• Hoe veranderen we die groeisnelheid? We schalen het met 4x (de macht van de exponent).

We kunnen onze groei omzetten in “e”-formaat: onze onmiddellijke groeisnelheid is ln(3), en we verhogen het tot ln(3) * 4. Nogmaals, de macht van de exponent (4) heeft onze groeisnelheid net geschaald.

Wanneer de bovenste exponent i is (zoals in $3^i$), vermenigvuldigen we gewoon onze impliciete groeisnelheid met i. Dus in plaats van te groeien met gewone ln(3), groeien we met ln(3) * i.

Het bovenste deel van de exponent wijzigt de impliciete groeisnelheid van het onderste deel.

The Nitty Gritty Details

Laten we het eens van dichterbij bekijken. Onthoud de definitie van e:

Die $100%}{n}$ staat voor het deel rente dat we in elke microscopische periode hebben verdiend. We gingen ervan uit dat de rente 100% was in de reële dimensie — maar wat als hij 100% was in de denkbeeldige richting?

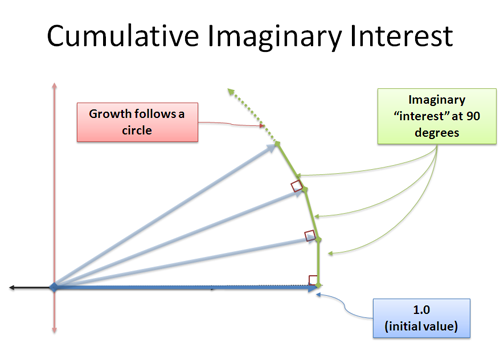
Nu voegt onze nieuw gevormde rente zich aan ons toe in de 90-graden richting. Verrassend genoeg verandert dit onze lengte niet — dit is een lastig begrip, want het lijkt een driehoek te maken waarvan de schuine zijde groter moet zijn. We hebben te maken met een limiet, en de extra afstand valt binnen de foutmarge die we aangeven. Dit is iets waar ik een andere dag op in wil gaan, maar neem van mij aan: continue loodrechte groei zal je roteren. Dit is de kern van sinus en cosinus, waar je verandering loodrecht op je huidige positie staat, en je in een cirkel beweegt.

We passen i eenheden van groei toe in oneindig kleine stappen, die ons elk een hoek van 90 graden opdrijven. Er is geen “sneller en sneller” draaien – in plaats daarvan kruipen we langs de omtrek over een afstand van |i| = 1 (grootte van i).

En hé — de afstand die rond een cirkel wordt gekropen is een hoek in radialen! We hebben een andere manier gevonden om cirkelvormige beweging te beschrijven!

Om cirkelvormige beweging te krijgen: Verander continu door te draaien in een hoek van 90 graden (aka imaginaire groeisnelheid).

Dus, Euler’s formule zegt “exponentiële, imaginaire groei trekt een cirkel”. En dit pad is hetzelfde als bewegen in een cirkel met behulp van sinus en cosinus in het denkbeeldige vlak.

In dit geval is het woord “exponentieel” verwarrend omdat we met een constante snelheid de cirkel rondreizen. In de meeste discussies wordt exponentiële groei verondersteld een cumulatief, samengesteld effect te hebben.

Een paar voorbeelden

Je gelooft me toch niet echt? Hier zijn een paar voorbeelden, en hoe u er intuïtief over kunt denken.

Voorbeeld: $e^i$

Waar is de x? Ah, het is gewoon 1. Intuïtief, zonder een rekenmachine te hoeven pakken, weten we dat dit betekent “reis 1 radiaal langs de eenheidscirkel”. In mijn hoofd zie ik “e” proberen om 1 te groeien met 100% in dezelfde richting, maar i blijft de bal bewegen en dwingt “1” om te groeien langs de rand van een cirkel:

Niet het mooiste getal, maar daar is het. Vergeet niet uw rekenmachine in radiaalstand te zetten als u dit intikt.

Voorbeeld: $3^i$

Dit is lastig — het is niet in ons standaardformaat. Maar onthoud,

We willen een initiële groei van 3x aan het eind van de periode, of een onmiddellijke groei van ln(3). Maar, de i komt langs en verandert die snelheid van ln(3) in “i * ln(3)”:

We dachten dat we gingen transformeren met een regelmatige snelheid van ln(3), een beetje sneller dan 100% continue groei omdat e ongeveer 2,718 is. Maar oh nee, ik heb ons omgedraaid: nu transformeren we met een denkbeeldige snelheid, wat betekent dat we gewoon ronddraaien. Als i een gewoon getal was, zoals 4, zou het ons 4x sneller hebben doen groeien. Nu groeien we met een snelheid van ln(3), maar zijwaarts.

We zouden een complex getal op de eenheidscirkel moeten verwachten — er is niets in de groeisnelheid dat ons groter maakt. De vergelijking oplossen:

In plaats van “1” eenheid rond de cirkel te eindigen (zoals $e^i$) eindigen we dus ln(3) eenheden rond.

Voorbeeld: $i^i$

Een paar maanden geleden zou ik hier tranen van in mijn ogen hebben gekregen. Vandaag niet! Laten we de transformaties afbreken:

We beginnen met 1 en willen dat veranderen. Zoals het oplossen van $3^i$, wat is het momentane groeipercentage met i als basis?

Hrm. Normaal gesproken zouden we ln(x) doen om de groeisnelheid te krijgen die nodig is om x te bereiken aan het eind van 1 tijdseenheid. Maar voor een denkbeeldig percentage? Daar moeten we even over nadenken.

Om met 1 te beginnen en naar i te groeien, moeten we vanaf het begin gaan roteren. Hoe snel? Wel, we moeten 90 graden (pi/2 radialen) in 1 tijdseenheid halen. Dus onze snelheid is $i \frac{\pi}{2}$. Onthoud dat onze snelheid denkbeeldig moet zijn, want we roteren, niet groeien! De gewone oude $\frac{\pi}{2}$ is ongeveer 1,57 en resulteert in een regelmatige groei.

Dit zou logisch moeten zijn: om 1,0 te veranderen in i aan het einde van 1 eenheid, moeten we $\frac{\pi}{2}$ radialen (90 graden) draaien in die hoeveelheid tijd. Om “i” te krijgen kunnen we dus $e^{i \frac{\pi}{2}}$ gebruiken.

Phew. Dat beschrijft i als de basis. Hoe zit het met de exponent?

Wel, de andere i vertelt ons dat we onze snelheid moeten veranderen — ja, die snelheid waar we zo lang over hebben nagedacht! Dus in plaats van te draaien met een snelheid van $i \frac{\pi}{2}$, wat een basis van i betekent, veranderen we de snelheid in:

De i’s heffen elkaar op en maken de groeisnelheid weer reëel! We hebben ons percentage gedraaid en onszelf in de negatieve getallen geduwd. En een negatieve groeisnelheid betekent dat we krimpen — we zouden verwachten dat $i^i$ dingen kleiner maakt. En dat doet het ook:

Tada! (Zoek “i^i” op Google om de rekenmachine te gebruiken)

Neem even adem: Je kunt intuïtief uitvinden hoe imaginaire basen en imaginaire exponenten zich moeten gedragen. Wauw.

En als bonus heb je ln(i) uitgedokterd — om $e^x$ i te laten worden, laat je e $\frac{\pi}{2}$ radialen draaien.

Voorbeeld: (i^i)^i

Een dubbele imaginaire exponent? Als je erop staat. Ten eerste weten we wat onze groeisnelheid binnen de haakjes zal zijn:

We krijgen een negatieve (krimpende) groeisnelheid van -pi/2. En nu wijzigen we die snelheid weer door i:

En nu hebben we een negatieve draaiing! We gaan de cirkel rond met een snelheid van $-\frac{\pi}{2}$ per tijdseenheid. Hoe lang gaan we nog? Wel, er is een impliciete “1” tijdseenheid helemaal bovenaan deze exponent keten; de impliciete standaard is om voor 1 tijdseenheid te gaan (net zoals $e = e^1$). 1 tijdseenheid geeft ons een rotatie van $-\frac{\pi}{2}$ radialen (-90 graden) of -i!

En, gewoon voor de lol, als we dat gekke resultaat kwadrateren:

Het is “gewoon” het dubbele van de rotatie: 2 is een regelmatig getal dus verdubbelt onze rotatiesnelheid tot een volledige -180 graden in een tijdseenheid. Of, je kunt het zien als twee keer achter elkaar -90 graden draaien.

Op het eerste gezicht zijn dit echt vreemde exponenten.

Complexe groei

We kunnen reële en imaginaire groei tegelijkertijd hebben: het reële deel schaalt ons op, en het imaginaire deel draait ons rond:

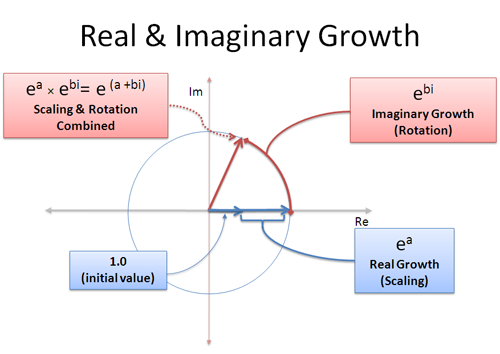
Een complexe groeisnelheid als (a + bi) is een mengeling van reële en imaginaire groei. Het reële deel a, betekent “groeien tegen 100% gedurende a seconden” en het imaginaire deel b betekent “roteren gedurende b seconden”. Denk eraan, rotaties hebben niet het voordeel van ‘compounding’, omdat je steeds in een andere richting ‘duwt’ — rotatie telt lineair op.

Met dit in gedachten, kunnen we elk punt op elke grootte cirkel voorstellen met (a+bi)! De straal is $e^a$ en de hoek wordt bepaald door $e^{bi}$. Het is alsof je het getal twee keer in de expand-o-tron stopt: één keer om het te laten groeien tot de juiste grootte (a seconden), een andere keer om het te roteren tot de juiste hoek (b seconden). Of, je kunt het eerst draaien en dan laten groeien!

Laten we zeggen dat we de groeisnelheid willen weten om tot 6 + 8i te komen. Dit is eigenlijk vragen naar de natuurlijke log van een imaginair getal: hoe laten we e groeien om (6 + 8i) te krijgen?

• Radius: Hoe groot moet de cirkel zijn? De grootte is $6^2 + 8^2} = \sqrt{100} = 10$. Wat betekent dat we moeten groeien voor ln(10) = 2,3 seconden om die hoeveelheid te bereiken.
• Wat is de hoek van dat punt? We kunnen arctan gebruiken om dat uit te rekenen: atan(8/6) = 53 graden = .93 radiaal.
• Combineer het resultaat: ln(6+8i) = 2.3 + .93i

Dat wil zeggen, we kunnen het willekeurige punt (6 + 8i) bereiken als we $e^{2.3 + .93i}$.

Waarom is dit nuttig?

De formule van Euler geeft ons een andere manier om beweging in een cirkel te beschrijven. Maar dat konden we al met sinus en cosinus – wat is er zo bijzonder?

Het heeft alles te maken met perspectief. Sinus en cosinus beschrijven beweging in termen van een raster, waarbij horizontale en verticale coördinaten worden uitgezet.

Eulers formule gebruikt poolcoördinaten — wat is je hoek en afstand? Nogmaals, het zijn twee manieren om beweging te beschrijven:

• Rastersysteem: Ga 3 eenheden naar het oosten en 4 eenheden naar het noorden
• Polaire coördinaten: Ga 5 eenheden in een hoek van 53,13 graden

Afhankelijk van het probleem zijn polaire of rechthoekige coördinaten bruikbaarder. De formule van Euler laat ons toe om te rekenen tussen de twee om het beste gereedschap voor de job te gebruiken. En omdat $e^{ix}$ kan worden omgerekend naar sinus en cosinus, kunnen we formules in de trigica herschrijven als variaties op e, wat erg handig is (je hoeft sin(a+b) niet uit je hoofd te leren, je kunt het afleiden — een andere keer meer). En het is mooi dat elk getal, reëel of complex, een variatie is van e.

Maar nut, schmut nut: het belangrijkste resultaat is het besef dat verbijsterende vergelijkingen intuïtief kunnen worden met de juiste analogieën. Laat mooie vergelijkingen zoals de formule van Euler geen toverspreuk blijven — bouw voort op de analogieën die je kent om de inzichten in de vergelijking te zien.

Happy math.

Appendix

De screencast was leuk, en feedback is zeker welkom. Ik denk dat het helpt de ideeën pop, en lopen door het artikel hielp me hiaten in mijn intuïtie te vinden.

• Brian Slesinsky heeft een nette presentatie over de formule van Euler
• Visual Complex Analysis heeft een geweldige discussie over de formule van Euler – zie p. 10 in de Google Book Preview
• Ik heb een lezing gedaan op Math and Analogies die de Identiteit van Euler meer visueel uitlegt:

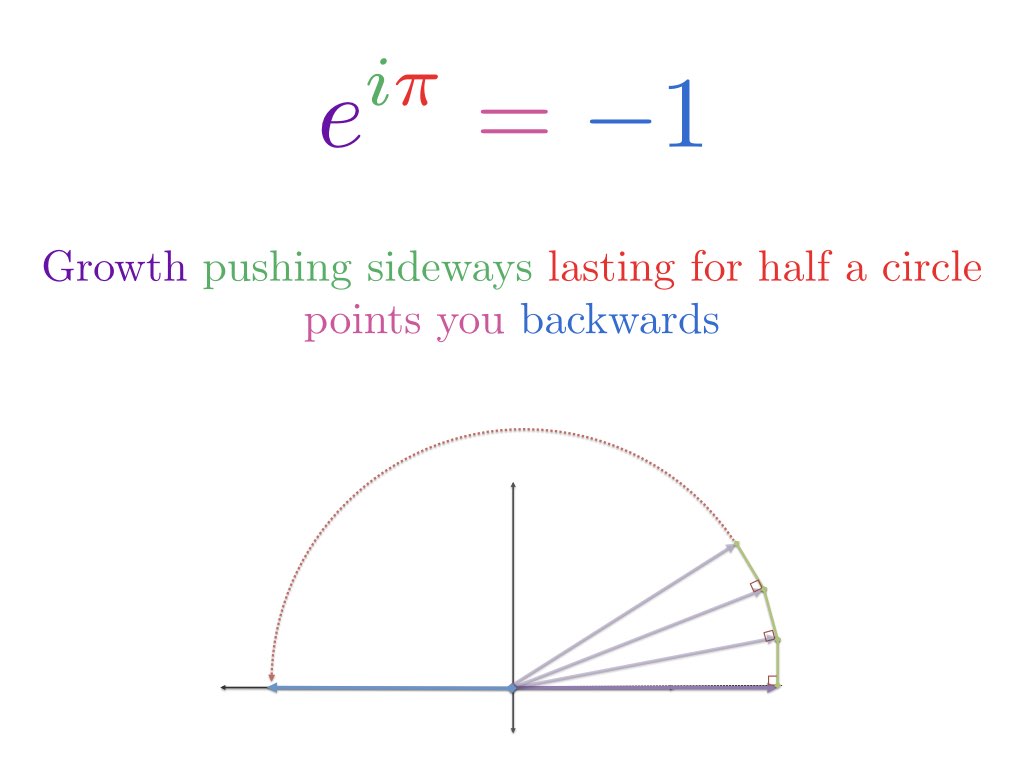
Andere berichten in deze serie

1. Een visuele, intuïtieve gids voor imaginaire getallen
2. Intuïtief rekenen met complexe getallen
3. Uitleg waarom complexe vermenigvuldiging werkt
4. Intuïtieve gids voor hoeken, Graden en Radialen
5. Intuïtief begrip van de formule van Euler
6. Een interactieve gids voor de Fourier-transformatie
7. Intuïtieve gids voor Convolutie
8. Intuïtief begrip van sinusgolven
9. Een intuïtieve gids voor lineaire algebra
10. De intuïtie van een programmeur voor matrixvermenigvuldiging
11. Imaginaire vermenigvuldiging vs. Imaginaire Exponenten