
Galileo wordt vaak beschouwd als de vader van de moderne wetenschap. Hij was degene die de beginselen van experiment, theorie en wiskunde samenbracht in een standaardkader. Waarschijnlijk meer dan wie ook was Galileo verantwoordelijk voor de ontwikkeling van de moderne wetenschap.
Het verhaal gaat dat Galileo twee stalen kogels van verschillende massa, maar van hetzelfde materiaal, vanaf de scheve toren van Pisa liet vallen en dat zij op hetzelfde moment landden. Wat opmerkelijk is aan dit experiment is dat hij een nieuwe methode van wetenschap bedrijven inluidde, waarbij je een experiment uitvoert om een hypothese te testen. Hij liet zien dat we meer moeten doen dan alleen maar denken dat iets waar is, maar dat we het ook moeten bewijzen.

Galileo vond een interessante paradox toen hij hoofd was van het departement wiskunde aan de universiteit van Pisa.
Definitie: Een paradox, ook wel antinomie genoemd, is een logisch met zichzelf in tegenspraak zijnde uitspraak of een uitspraak die tegen iemands verwachting ingaat. (Wikipedia). (Grieks: “para” = voorbij, “doxa” = geloof)
Galileo’s paradox ging over de vraag of twee verzamelingen die oneindig veel objecten bevatten, gelijkwaardig aan elkaar zijn. Stel bijvoorbeeld dat P de verzameling van positieve gehele getallen is waarbij P= {0,1,2,3,…} en E de verzameling van even getallen waarbij E = {0,2,4,6,…}. Galileo beweerde dat de grootte van deze twee verzamelingen gelijk zal zijn omdat we elk positief geheel getal uit de verzameling P kunnen paren aan de even getallen uit de verzameling E.

Hoe kan de grootte van de twee verzamelingen dan gelijk zijn als er een “minder” getal in E voorkomt? Dit werd de Galileo-paradox genoemd en startte een nieuw debat over het begrip oneindigheid.
Na Galileo werd zijn leerling Evangelista Torricelli hoofd van het Departement Wiskunde aan de Universiteit van Pisa. U kent hem misschien van zijn werken over de atmosferische druk en de uitvinding van de barometer. Aangezien Toricelli ook in wiskunde geïnteresseerd is, vraagt hij zich af:
Is het mogelijk een voorwerp te hebben met een eindig volume en een oneindig oppervlak? In de eerste plaats lijkt zoiets onwaarschijnlijk voor de meesten van ons. De wiskunde vertelt ons echter dat zoiets zou kunnen. Torricelli beantwoordde zijn vraag zelf en ontdekte Toricelli’s Trompet waarvan de oppervlakte oneindig is, maar waarvan het volume eindig is. Zijn ontdekking werd gezien als een “ongelooflijke” paradox.
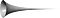
Er is trouwens een essentiële regel in de filosofie van de wiskunde; met welk tijdperk van de filosofie of de wiskunde je je ook bezighoudt, het houdt verband met de geschiedenis, de cultuur en de religie van dat gebied. Daarom noemen ze Toricelli’s trompet ook wel Gabriel’s hoorn. Er wordt hier verwezen naar de Bijbel omdat de christenen geloven dat de engel Gabriël op de hoorn zal blazen op de Dag des Oordeels.
Dus hoe vormt de Toricelli’s trompet zich? We weten allemaal hoe je een grafiek maakt van y=x. Als je in plaats daarvan een grafiek maakt van de vergelijking y=1/x waarbij x groter of gelijk is aan 1, ziet de grafiek er als volgt uit:
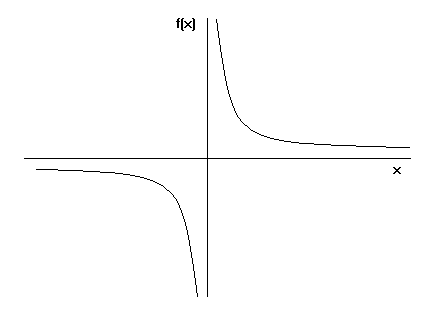
Wanneer we de grafiek van y=1/x nemen en om de x-as draaien, zien we de trompet van Toricelli.

Gelukkig hebben we wiskundige formules in handen om de oppervlakte en het volume van de trompet van Toricelli te berekenen. Wanneer we onderstaande integratieformule toepassen voor het volume van de trompet, krijgen we een eindige hoeveelheid.
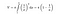
Wanneer we echter onderstaande integratieformule toepassen voor de oppervlakte van de trompet, dan wordt de oppervlakte van de trompet dit keer oneindig. Is dit resultaat niet interessant?
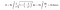
Omdat het volume van Toricelli’s trompet eindig is, kunnen we het vullen met een eindige hoeveelheid verf. Laten we bijvoorbeeld aannemen dat het volume van de trompet 100 liter is. Ik ga naar Home Depot en koop 100 liter verf en vul hem. Wat dit echter interessant maakt, is dat ik met die 100 liter verf een oneindig oppervlak zal hebben geverfd. Tegenwoordig noemen de meeste mensen deze paradox, “de schildersparadox.”
Houston, we hebben hier een probleem! De situatie die onmogelijk is in de praktijk wordt mogelijk in de wiskunde. Dus, hoe kan Torricelli’s trompet echt zijn? Of, hoe kunnen we alle elementen van de verzamelingen precies overeen laten komen terwijl een van de verzamelingen een deelverzameling is van een andere in Galileo’s voorbeeld?
De reden voor al deze conflicten is dat het begrip oneindigheid niet lijkt op andere begrippen die we kennen, en dat brengt veel mensen in verwarring. Galileo zegt voor zijn paradox,
“Ja, mijn vriend, er is oneindigheid. Het is zinloos daar iets tegenin te brengen. De verzamelingen waar ik aan werk zijn voorbeelden van gesloten verzamelingen waarbij oneindigheid een rol speelt. Ze beginnen bij een punt en gaan door tot in het oneindige, en toch zijn ze nog steeds verzameling. Mijn opmerkingen en begrippen over oneindigheid moeten echter anders zijn dan die ik zou gebruiken voor eindige grootheden. Als je te maken hebt met eindige grootheden, kun je zeggen dat 3 kilo minder is dan 5 kilo, of dat 32 meter langer is dan 7 meter. Maar als het om oneindigheid gaat, kun je niet zeggen dat deze oneindigheid groter, kleiner of gelijk is aan die.”
Dat was de oplossing van Galileo in de jaren 1600.
Helaas was met Galileo’s oplossing een nieuw debat over oneindigheid begonnen. Wiskundigen en filosofen konden het niet eens worden over een specifiek antwoord totdat Cantor zijn “verzamelingenleer” deelde, die leerlingen vandaag de dag op de basisschool leren.
We kunnen de ontwikkeling van het idee van oneindigheid periodiek historiseren. Het ontstond bij de Eleaten, een pre-Socratische filosofische school die door Parmenides in het begin van de vijfde eeuw v.C. in de oude stad Elea werd gesticht. Er waren drie grote filosofen in deze school, zoals Zeno, Xenophanes, en Parmenides. In deze school was de gangbare filosofie dat het bestaan enkelvoudig was, en er geen meervoudigheid bestond. Zeno was beroemd om zijn paradoxen over oneindigheid bij de Eleatica. Later in de jaren 300 voor Christus.., kwam Aristoteles op en stelde een tweetal begrippen voor om Zeno’s paradoxen te verklaren, namelijk potentiële oneindigheid en feitelijke oneindigheid.
De potentiële oneindigheid is een groep getallen of een groep “dingen” die doorgaat zonder te eindigen, doorgaat of zich steeds herhaalt zonder herkenbaar eindpunt.
Het feitelijke oneindige betreft nooit eindigende reeksen of “dingen” binnen een ruimte die een begin en een eind heeft; het is een reeks die technisch “voltooid” is, maar uit een oneindig aantal leden bestaat.
Aristoteles geloofde dat er geen feitelijke oneindigheid bestond. Dit idee van Aristoteles beheerste de wereld van de filosofie tot de jaren 1600. Toen beweerden filosofen als Cusa en Bruno dat er wel degelijk oneindigheid bestond, maar dat wij daar geen wijs uit konden worden. Na Cusa en Bruno mengde de grote denker Spinoza zich in het onderwerp.
Spinoza zei dat we het concept van oneindigheid konden begrijpen en ze in grootte konden rangschikken. Hij verklaarde echter ook dat hij ze niet kon uitrekenen. Hij kon bijvoorbeeld 3 bij 5 optellen, maar hij kon de ene oneindigheid niet bij de andere optellen.
Tot slot van deze debatten kwam er een knappe man, Georg Cantor, die de verzamelingenleer vond, die nog steeds de basis van de wiskunde is. Hij zette het laatste punt in de oneindigheidsdiscussies met zijn verzamelingenleer.
Hij toonde ons aan dat een oneindige verzameling groter of kleiner zou zijn dan een andere oneindige verzameling. Bovendien beweerde Cantor dat we oneindige verzamelingen konden optellen en vermenigvuldigen. Tot die tijd had de mens de ideeën van Aristoteles over oneindigheid gevolgd. Volgens Aristoteles zou het getal 3 weer oneindig zijn als we het met oneindig vermenigvuldigden. De oneindigheid zou alles opslokken. Op grond hiervan beweerde hij dat er alleen potentiële oneindigheid zou zijn, geen werkelijke oneindigheid.
Het tegendeel van Aristoteles’ idee bewees Cantor ons echter met de verzamelingenleer. Als we één toevoegen aan een oneindige verzameling, zal het niet meer dezelfde verzameling zijn. Hij probeerde de oneindigheden te vergelijken. Zo bewees Cantor dat de verzameling van alle functies van (0,1)→ℕ aftelbaar is. Zo definieerde hij een één-op-één en onto-functie van het interval (0,1) naar natuurlijke getallen.
Met andere woorden, hij bewees dat alle natuurlijke getallen tussen 0 en 1 kunnen passen omdat er oneindig veel rationale getallen tussen 0-1 waren, en deze oneindigheden kunnen aan elkaar worden gekoppeld. Toen deed hij iets wat nog gevaarlijker was dan het vinden van twee gelijke oneindigheden. Hij vergeleek de oneindigheid van de reële getallen met de oneindigheid van de natuurlijke getallen en ontdekte dat de oneindigheid van de reële getallen groter is dan de andere. Hij keek zelfs naar zijn bewijs en zei tegen zijn vriend Dedekind: “Ik zie het, maar zelfs ik kan het niet geloven…”.
Cantor was ook een wiskundige met zeer serieuze filosofische en religieuze zorgen. Tijdens het ontwikkelen van de verzamelingenleer zei hij: “God dicteerde mij de verzamelingenleer”.
De verzamelingenleer werd niet algemeen geaccepteerd toen deze voor het eerst werd ontwikkeld. Bedrijven namen Cantor niet eens aan voor een baan. Een wiskundige, Henri Poincaré, zei ooit: “De ideeën van deze Cantor zijn een slechte ziekte die aan de kraag van de wiskunde kleeft. En de wiskunde zal hem op een dag behandelen”. Cantor moest een tijdje naar een psychiatrische inrichting en stierf daar. Maar vandaag beschouwen we hem als een genie.
Cantor was een eenzame man aan de rand van de oneindigheid. Hij citeerde de Bijbel aan het begin van zijn artikel over oneindige getallen: “Alles wat verborgen is, zal aan het licht gebracht worden.”