Objetivos de Aprendizagem
- Para entender a representação 3D das orbitais eletrônicas
Um orbital é o refinamento mecânico quântico da órbita de Bohr. Ao contrário do seu conceito de uma órbita circular simples com um raio fixo, os orbitais são regiões matematicamente derivadas do espaço com diferentes probabilidades de conter um electrão.
Uma forma de representar as distribuições de probabilidade de electrões foi ilustrada anteriormente para o orbital 1s de hidrogénio. Como Ψ2 dá a probabilidade de encontrar um electrão num determinado volume de espaço (como um picómetro cúbico), um gráfico de Ψ2 versus distância do núcleo (r) é um gráfico da densidade de probabilidade. O orbital 1s é esférico simétrico, portanto a probabilidade de encontrar um elétron 1s em um determinado ponto depende apenas da sua distância do núcleo. A densidade de probabilidade é maior em \\(r) = 0\) (no núcleo) e decresce constantemente com o aumento da distância. A valores muito grandes de r, a densidade de probabilidade dos electrões é muito pequena mas não nula.
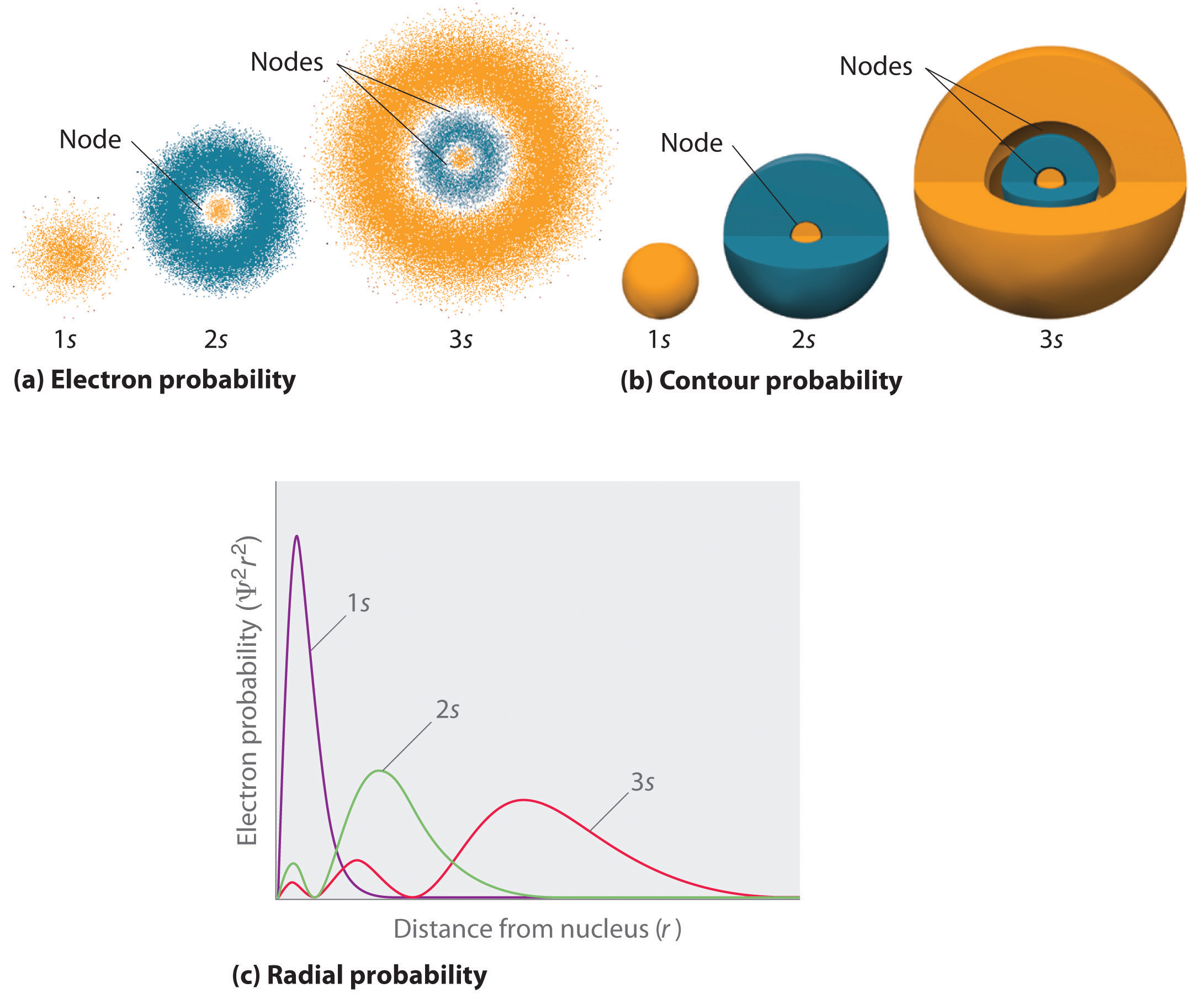
Em contraste, podemos calcular a probabilidade radial (a probabilidade de encontrar um electrão 1s a uma distância \(r) do núcleo) adicionando em conjunto as probabilidades de um electrão estar em todos os pontos numa série de x conchas esféricas de raio r1, r2, r3,…, rx – 1, rx. Com efeito, estamos a dividir o átomo em conchas concêntricas muito finas, muito semelhantes às camadas de uma cebola (Figura 1a), e a calcular a probabilidade de encontrar um electrão em cada concha esférica. Recorde-se que a densidade de probabilidade dos elétrons é maior em 0 (Figura 1b), portanto a densidade de pontos é maior para as menores conchas esféricas em parte (a) da Figura 1b). Em contraste, a área de superfície de cada concha esférica é igual a (4πr^2), o que aumenta muito rapidamente com o aumento (r) (Figura 1c)). Como a área da superfície das conchas esféricas aumenta mais rapidamente com o aumento da densidade de probabilidade de electrões do que com a diminuição da densidade de probabilidade de electrões, o gráfico de probabilidade radial tem um máximo a uma distância de partículas (Figura 1d)). Mais importante, quando a(r) é muito pequena, a superfície de uma concha esférica é tão pequena que a probabilidade total de encontrar um elétron próximo ao núcleo é muito baixa; no núcleo, a probabilidade do elétron desaparece (Figura \PageIndex{1d}}).

Fo(r\) o átomo de hidrogênio, o pico no gráfico de probabilidade radial ocorre em \(r\) = 0,529 Å (52,9 pm), que é exatamente o raio calculado por Boh(r\) fo(r\) o n = 1 órbita. Assim, o raio mais provável obtido pela mecânica quântica é idêntico ao raio calculado pela mecânica clássica. No modelo de Bohr, no entanto, supôs-se que o elétron está a esta distância 100% do tempo, enquanto que no modelo de Schrödinge, está a esta distância apenas uma parte do tempo. A diferença entre os dois modelos é atribuível ao comportamento ondulatório do elétron e ao princípio de incerteza de Heisenberg.
Figure {2}) compara as densidades de probabilidade de elétrons das orbitais de hidrogênio 1s, 2s e 3s. Note que todos os três são esféricos simétricos. Para as orbitais dos 2s e 3s, a densidade de probabilidade dos elétrons não cai suavemente com o aumento das orbitais dos 3s. Ao invés disso, uma série de mínimos e máximos são observados nos gráficos de probabilidade radial (Figura 2c). Os mínimos correspondem aos nós esféricos (regiões de probabilidade zero de elétrons), que se alternam com regiões esféricas de probabilidade não zero de elétrons. A existência destes nós é uma consequência das mudanças de fase da onda na função de onda Ψ.
s Orbitais (l=0)
Três coisas acontecem aos orbitais de s conforme n aumenta (Figura \PageIndex{2}):
- Eles se tornam maiores, estendendo-se para peidos a partir do núcleo.
- Contêm mais nós. Isto é semelhante a uma onda de pé que tem regiões de amplitude significativa separadas por nós, pontos com amplitude zero.
- Fo(r) um dado átomo, os orbitais também se tornam altos em energia à medida que n aumenta por causa do aumento da distância do núcleo.
Os orbitais são geralmente desenhados como superfícies tridimensionais que envolvem 90% da densidade de elétrons, como foi mostrado para os orbitais de hidrogênio 1s, 2s, e 3s em parte (b) na Figura {2}(PageIndex{2}). Embora tais desenhos mostrem os tamanhos relativos das orbitais, eles normalmente não mostram os nós esféricos nas orbitais 2s e 3s porque os nós esféricos estão dentro da superfície de 90%. Felizmente, as posições dos nós esféricos não são importantes para a ligação química.
p Orbitais (l=1)
Apenas os orbitais s são esféricos simétricos. À medida que o valor de l aumenta, o número de orbitais num determinado subsolo aumenta, e as formas dos orbitais tornam-se mais complexas. Como a subesfera 2p tem l = 1, com três valores de ml (-1, 0 e +1), existem três orbitais 2p.
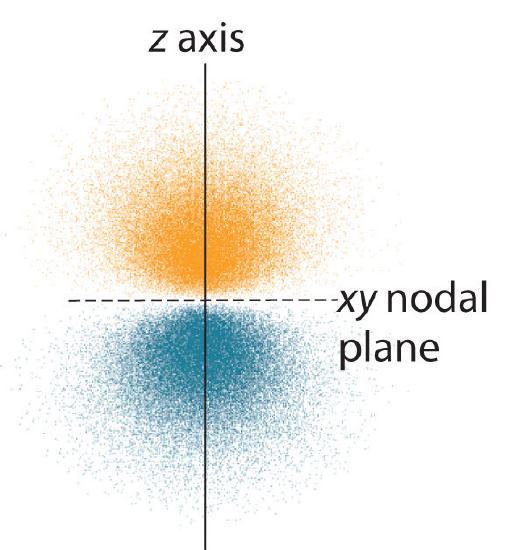
A distribuição de probabilidade de elétrons de um dos orbitais de hidrogênio 2p é mostrada na Figura 3. Como este orbital tem dois lóbulos de densidade de elétrons dispostos ao longo do eixo z, com uma densidade de elétrons de zero no plano xy (ou seja, o plano xy é um plano nodal), ele é um orbital \(2p_z). Como mostra a Figura 4, os dois orbitais 2p têm formas idênticas, mas encontram-se ao longo do eixo x (2p_x) e do eixo y (2p_y), respectivamente. Note que cada orbital p tem apenas um plano nodal. Em cada caso, a fase da função de onda para cada um dos orbitais 2p é positiva para o lóbulo que aponta ao longo do eixo positivo e negativa para o lóbulo que aponta ao longo do eixo negativo. É importante salientar que estes sinais correspondem à fase da onda que descreve o movimento dos elétrons, não a cargas positivas ou negativas.
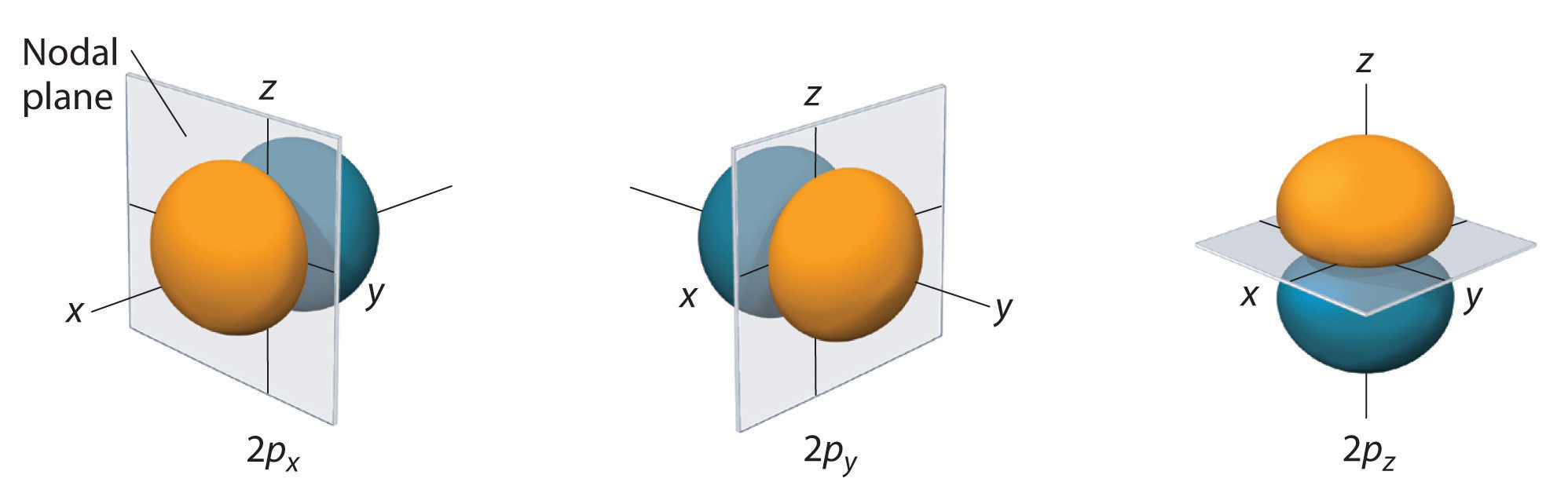
The surfaces shown enclose 90% of the total electron probability fo(r\) the 2px, 2py, and 2pz orbitals. Cada orbital é orientado ao longo do eixo indicado pelo subscrito e um plano nodal que é perpendicular a esse eixo bissecta cada orbital de 2px. A fase da função de onda é positiva (laranja) na região do espaço onde x, y, o z é positivo e negativo (azul) onde x, y, o z é negativo. Tal como nas orbitais s, o tamanho e complexidade das orbitais p de qualquer átomo aumenta à medida que o número quântico principal n aumenta. As formas das superfícies de 90% de probabilidade das orbitais 3p, 4p e p de maior energia são, no entanto, essencialmente as mesmas que as mostradas na Figura \(\PageIndex{4}}.
d Orbitais (l=2)
Subshells com l = 2 têm cinco d orbitais; a primeira concha principal a ter um d sub-shell corresponde a n = 3. Os cinco orbitais d têm valores ml de -2, -1, 0, +1 e +2,
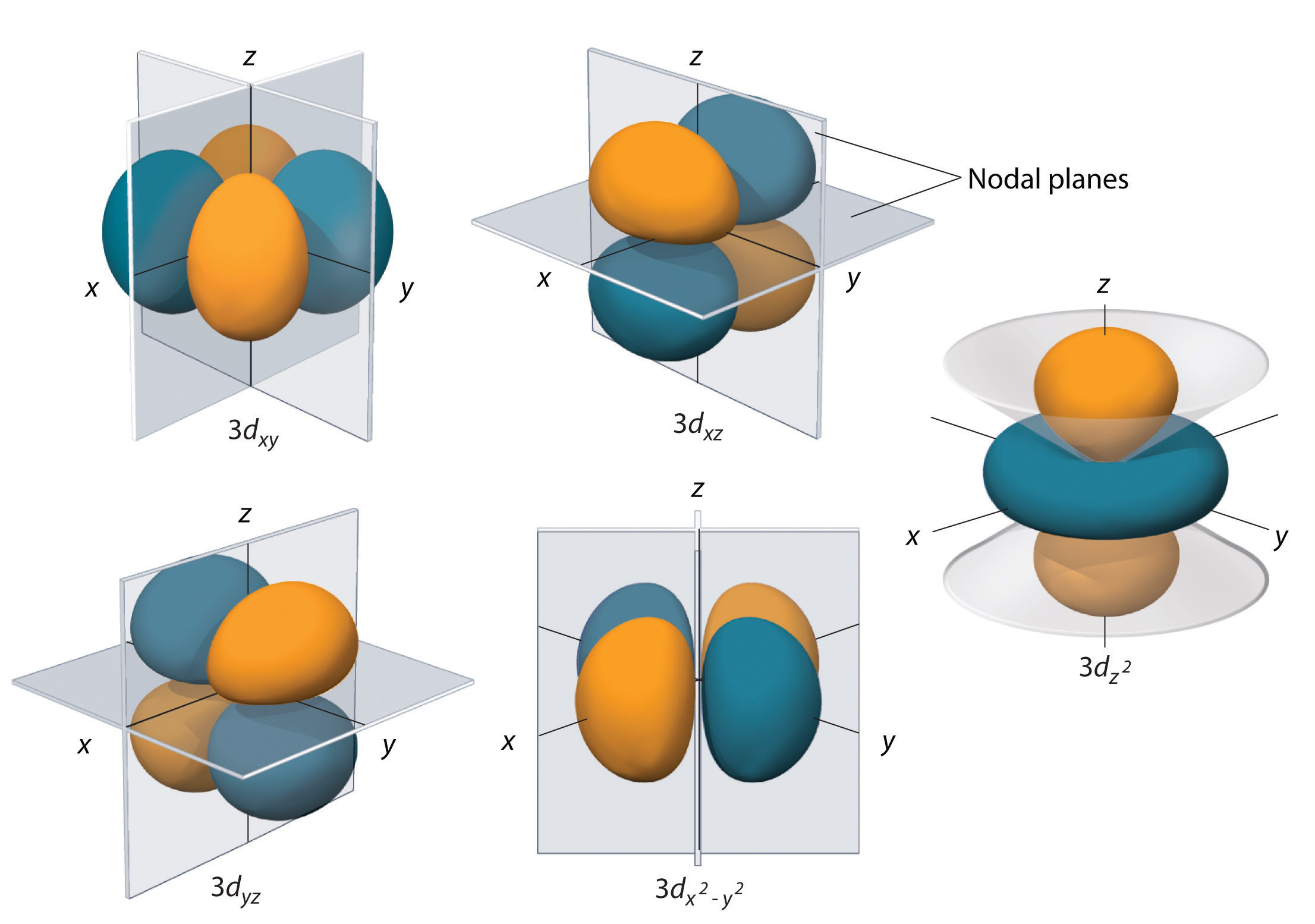
Os orbitais 3d de hidrogênio, mostrados na Figura 5, têm formas mais complexas que os orbitais 2p. Todas as cinco orbitais 3d contêm duas superfícies nodais, em comparação com uma orbital p e zero orbital s. Em três dos orbitais d, os lóbulos de densidade de elétrons são orientados entre os planos x e y, x e z, e y e z; esses orbitais são chamados de orbitais {3d_{xy}, {xz})3d_, e {xz_), respectivamente. Um quarto orbital d tem lóbulos ao longo dos eixos x e y; este é o orbital {x^2-y^2}(3d_{x^2-y^2}). O quinto orbital 3d, chamado orbital {\i1}(3d_{z^2}}, tem uma forma única: parece um orbital {\i}(2p_z} combinado com um donut adicional de probabilidade de electrões deitado no plano xy. Apesar da sua forma peculiar, o orbital é matematicamente equivalente ao orbital de fou e tem a mesma energia. Em contraste com os orbitais p, a fase da função de onda dos orbitais d é a mesma dos pares de lóbulos opostos. Como mostrado na Figura 5, a fase da função de onda é positiva para os dois lóbulos do orbital que estão ao longo do eixo z, enquanto a fase da função de onda é negativa para o donut da densidade de elétrons no plano xy. Como os orbitais s e p, conforme n aumenta, o tamanho dos orbitais d aumenta, mas as formas gerais permanecem semelhantes às representadas na Figura \\(\PageIndex{5}}.
f Orbitais (l=3)
Conchas primitivas com n = 4 podem ter subconchas com l = 3 e valores ml de -3, -2, -1, 0, +1, +2, e +3. Estas subcascasas consistem em sete orbitais. Cada f orbital tem três superfícies nodais, portanto as formas são complexas. Porque f orbitais não são particularmente importantes para os propósitos, não os discutimos mais, e orbitais com altos valores de l não são discutidos de forma alguma.
Energia orbital
Embora tenhamos discutido as formas de orbitais, pouco temos dito sobre as energias comparativas de f orbitais. Começamos a discussão das energias orbitais considerando átomos de iões com apenas um electrão (como o H o+).
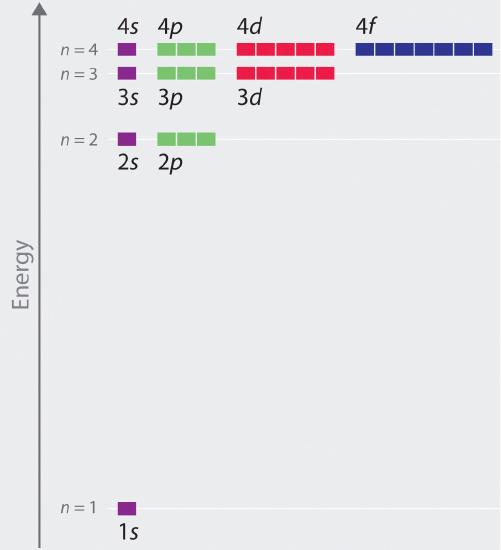
As energias relativas das orbitais atómicas com n ≤ 4 fo(r) um átomo de hidrogénio estão representadas na Figura 6; note-se que as energias orbitais dependem apenas do principal numeral quântico n. Consequentemente, as energias das orbitais 2s e 2p de hidrogênio são as mesmas; as energias das orbitais 3s, 3p e 3d são as mesmas; e assim por diante. A mecânica quântica prevê que no átomo de hidrogênio, todas as orbitais com o mesmo valor de n (por exemplo, as três orbitais 2p) são degeneradas, significando que elas têm a mesma energia. As energias orbitais obtidas pelo hidrogênio usando a mecânica quântica são exatamente as mesmas que as energias permitidas calculadas por Boh (r). Ao contrário do modelo de Bohr, que permitiu apenas uma órbita para cada nível de energia, a mecânica quântica prevê que existem 4 orbitais com diferentes distribuições de densidade de elétrons no n = 2 casco principal (um 2s e três 2p orbitais), 9 no n = 3 casco principal, e 16 no n = 4 casco principal.Os diferentes valores de l e ml das orbitais individuais dentro de uma determinada concha principal não são importantes para entender os espectros de absorção de emissão de átomos de hidrogênio, mas explicam as divisões das linhas principais que são observadas quando átomos de hidrogênio são colocados em um campo magnético. A Figura 6 mostra que os níveis de energia se tornam próximos e próximos à medida que o valor de n aumenta, como esperado devido à dependência 1/n2 das energias orbitais.
Em geral, tanto a energia como o raio diminuem à medida que a carga do núcleo aumenta. Assim, os orbitais mais estáveis (aqueles com menor energia) são os mais próximos do núcleo. Por exemplo, no estado de terra do átomo de hidrogênio, o elétron único está na órbita 1s, enquanto que no primeiro estado excitado, o átomo absorveu energia e o elétron foi promovido a um dos n = 2 orbitais. Em iões com apenas um electrão, a energia de um determinado orbital depende apenas de n, e todas as subcasas dentro de uma concha principal, tais como as orbitais {p_x}, {p_y} e {p_z}, são degeneradas.
Sumário
Os tipos de orbitais atómicos quimicamente importantes correspondem a valores de {\i}, {\i1}(1}), {\i}(2}, e {\i3}. Os orbitais com {\i1}(1}ell = 0}) são orbitais s e são esféricos simétricos, com a maior probabilidade de encontrar o elétron ocorrendo no núcleo. Todos os orbitais com valores de { n > 1} e { ell = 0} contêm um ou mais nós. Os orbitais com \(n > 1\) são orbitais p e contêm um plano nodal que inclui o núcleo, dando origem a uma forma de haltere. Orbitais com órbita = 2 são orbitais e têm formas mais complexas com pelo menos duas superfícies nodais. Os orbitais com {\i1}(\i1 = 3\i} são orbitais, que são ainda mais complexos.
Porque sua distância média do núcleo determina a energia de um elétron, cada orbital atômico com um determinado conjunto de números quânticos tem uma energia particulada associada a ele, a energia orbital.
Contribuidores e Atribuições
-
Modificado por Joshua Halpern (Universidade Howard)