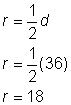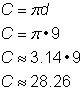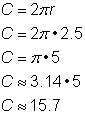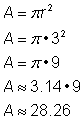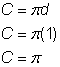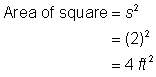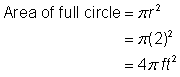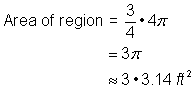Círculos
Objectivo(s) de aprendizagem
– Identificar as propriedades dos círculos.
– Encontrar a circunferência de um círculo.
– Encontrar a área de uma circunferência.
– Encontrar a área e perímetro de figuras geométricas compostas.
Introdução
Círculos são uma forma comum. Vê-se todos sobre rodas em um carro, Frisbees passando através do ar, discos compactos entregando dados. Estes são todos círculos.
Um círculo é uma figura bidimensional tal como os polígonos e quadriláteros. No entanto, os círculos são medidos de forma diferente destas outras formas – você tem até que usar alguns termos diferentes para descrevê-los. Vamos dar uma olhada nesta interessante forma.
Propriedades de Círculos
Uma circunferência representa um conjunto de pontos, todos eles estão à mesma distância de um ponto fixo, do meio. Este ponto fixo é chamado de centro. A distância do centro da circunferência a qualquer ponto da circunferência é chamada de raio.
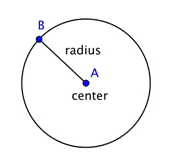
Quando dois raios (o plural do raio) são colocados juntos para formar um segmento de linha através da circunferência, você tem um diâmetro. O diâmetro de uma circunferência passa pelo centro da circunferência e tem os seus pontos finais na própria circunferência.
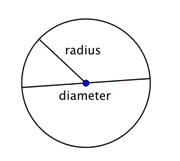
O diâmetro de qualquer circunferência é duas vezes o comprimento do raio dessa circunferência. Pode ser representado pela expressão 2r, ou “duas vezes o raio”. Então se você conhece o raio de uma circunferência, você pode multiplicá-lo por 2 para encontrar o diâmetro; isto também significa que se você conhece o diâmetro de uma circunferência, você pode dividir por 2 para encontrar o raio.
|
Exemplo |
||
|
Problema |
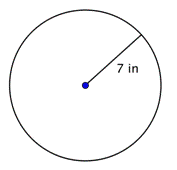
Findir o diâmetro da circunferência. > |
|
|
d = 2r d = 2(7) d = 14 |
O diâmetro é duas vezes o raio, ou 2r. O raio deste círculo é de 7 polegadas, portanto o diâmetro é 2(7) = 14 polegadas. |
|
|
Resposta |
O diâmetro é de 14 polegadas. |
|
|
Exemplo |
||
|
Problema |
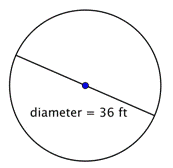
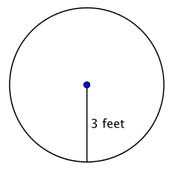
Realizar o raio do círculo.
|
|
|
|
O raio é metade do diâmetro, ou |
|
|
Resposta |
O raio é de 18 pés. |
|
Circunferência
A distância à volta de um círculo é chamada circunferência. (Lembre-se, a distância ao redor de um polígono é o perímetro.)
Uma propriedade interessante sobre círculos é que a proporção da circunferência de um círculo e seu diâmetro é o mesmo para todos os círculos. Não importa o tamanho da circunferência, a razão da circunferência e diâmetro será a mesma.
Algumas medidas reais de diferentes itens são fornecidas abaixo. As medidas são precisas para o milímetro ou quarto de polegada mais próximo (dependendo da unidade de medida utilizada). Observe a razão da circunferência para o diâmetro de cada um dos itens – embora os itens sejam diferentes, a razão para cada um é aproximadamente a mesma.
|
Item |
Circunferência (C) (arredondada ao centésimo) |
diâmetro (d) |
Ratio |
|
Cup |
253 mm |
79 mm |
|
|
Quarter |
84 mm |
27 mm |
|
|
Bowl |
37.25 em |
11,75 em |
|
A circunferência e o diâmetro são medidas aproximadas, uma vez que não existe uma forma precisa de medir exactamente estas dimensões. Se você fosse capaz de medí-las com mais precisão, contudo, você descobriria que a razão ![]() se moveria para 3,14 para cada um dos itens dados. O nome matemático para a razão
se moveria para 3,14 para cada um dos itens dados. O nome matemático para a razão ![]() é pi, e é representado pela letra grega
é pi, e é representado pela letra grega ![]() .
.
![]() é um decimal não terminante, não repetitivo, por isso é impossível escrevê-lo completamente. Os primeiros 10 dígitos de
é um decimal não terminante, não repetitivo, por isso é impossível escrevê-lo completamente. Os primeiros 10 dígitos de ![]() são 3,141592653; é frequentemente arredondado para 3,14 ou estimado como a fração
são 3,141592653; é frequentemente arredondado para 3,14 ou estimado como a fração ![]() . Note que tanto 3,14 como
. Note que tanto 3,14 como ![]() são aproximações de
são aproximações de![]() , e são usados em cálculos onde não é importante ser preciso.
, e são usados em cálculos onde não é importante ser preciso.
Desde que você saiba que a razão entre circunferência e diâmetro (ou ![]() ) é consistente para todos os círculos, você pode usar este número para encontrar a circunferência de um círculo se você souber o seu diâmetro.
) é consistente para todos os círculos, você pode usar este número para encontrar a circunferência de um círculo se você souber o seu diâmetro.
![]() =
= ![]() , então C =
, então C = ![]() d
d
>Tambem, desde d = 2r, então C = ![]() d =
d = ![]() (2r) = 2
(2r) = 2![]() r.
r.
Circunferência de um círculo
Para encontrar a circunferência (C) de um círculo, use uma das seguintes fórmulas:
Se você souber o diâmetro (d) de um círculo: ![]()
Se souber o raio (r) de uma circunferência: ![]()
|
Exemplo |
||
|
Problema |
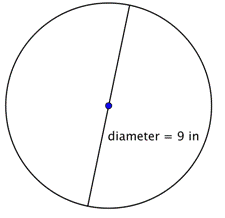
>Ponhamos a circunferência da circunferência.
|
|
|
|
Para calcular a circunferência dada um diâmetro de 9 polegadas, use a fórmula Desde que você esteja usando uma aproximação para |
|
|
Resposta |
A circunferência é 9 |
|
|
Exemplo |
||
|
Problema |
Passar a circunferência de uma circunferência com um raio de 2.5 jardas. |
|
|
|
Para calcular a circunferência de uma circunferência com um raio de 2,5 jardas, use a fórmula |
|
|
Resposta |
A circunferência é de 5 |
|
Uma circunferência tem um raio de 8 polegadas. Qual é a sua circunferência, arredondada para a polegada mais próxima?
A) 25 polegadas
B) 50 polegadas
C) 64 polegadas2
D) 201 polegadas
Área
![]() é um número importante na geometria. Você já o usou para calcular a circunferência de um círculo. Você usa
é um número importante na geometria. Você já o usou para calcular a circunferência de um círculo. Você usa ![]() quando você está descobrindo a área de um círculo, também.
quando você está descobrindo a área de um círculo, também.
Área de um Círculo
Para encontrar a área (A) de um círculo, use a fórmula: ![]()
|
Exemplo |
||
|
Problema |
Encontrar a área do círculo.
|
|
|
|
Para encontrar a área deste círculo, use a fórmula Lembrar de escrever a resposta em termos de unidades quadradas, já que você está encontrando a área. |
|
|
Resposta |
A área é 9 |
|
Um botão tem um diâmetro de 20 milímetros. Qual é a área do botão? Use 3.14 como uma aproximação de ![]() .
.
A) 62,8 mm
B) 314 mm2
C) 400 mm2
D) 1256 mm2
Figuras compostas
Agora que você saiba calcular a circunferência e a área de um círculo, você pode usar esse conhecimento para encontrar o perímetro e a área das figuras compostas. O truque para descobrir esses tipos de problemas é identificar formas (e partes de formas) dentro da figura composta, calcular suas dimensões individuais e depois adicioná-las juntas.
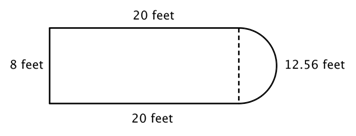
Por exemplo, veja a imagem abaixo. É possível encontrar o perímetro?
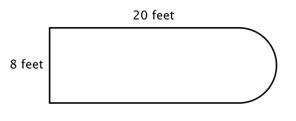
O primeiro passo é identificar figuras mais simples dentro desta figura composta. Você pode dividi-la em um retângulo e um semicírculo, como mostrado abaixo.
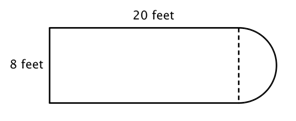
Você sabe como encontrar o perímetro de um retângulo, e você sabe como encontrar a circunferência de um círculo. Aqui, o perímetro dos três lados sólidos do retângulo é 8 + 20 + 20 = 48 pés. (Note que apenas três lados do retângulo irão adicionar ao perímetro da figura composta porque o outro lado não está em uma borda; ele é coberto pelo semicírculo!)
Para encontrar a circunferência do semicírculo, use a fórmula ![]() com um diâmetro de 8 pés, então pegue metade do resultado. A circunferência do semicírculo é
com um diâmetro de 8 pés, então pegue metade do resultado. A circunferência do semicírculo é ![]() , ou aproximadamente 12,56 pés, portanto o perímetro total é de cerca de 60,56 pés.
, ou aproximadamente 12,56 pés, portanto o perímetro total é de cerca de 60,56 pés.
|
Exemplo |
||
|
Problema |
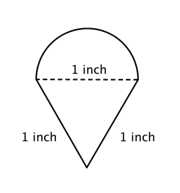
Realizar o perímetro (ao centésimo mais próximo) da figura composta, constituída por um semicírculo e um triângulo.
|
|
|
|
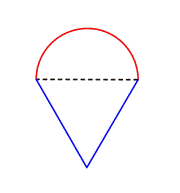
Identificar formas menores dentro da figura composta. Esta figura contém um semicírculo e um triângulo. |
|
|
Diametro (d) = 1
Circunferência do semicírculo = |
Passar a circunferência do círculo. Depois divida por 2 para encontrar a circunferência do semicírculo. |
|
|
|
|
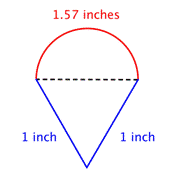
Circunferência total do perímetro adicionando a circunferência do semicírculo e os comprimentos das duas pernas. Como a nossa medida da circunferência do semicírculo é aproximada, o perímetro também será uma aproximação. |
|
Resposta |
Aproximadamente 3.57 polegadas |
|
|
Exemplo |
||
|
Problema |
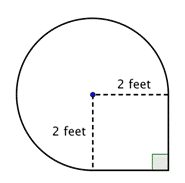
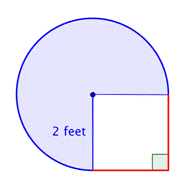
>Encontrar a área da figura composta, composto por três quartos de um círculo e um quadrado, até ao centésimo mais próximo.
|
|
|
|
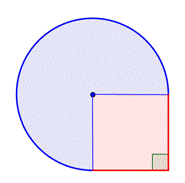
Identificar formas menores dentro da figura composta. Esta figura contém uma região circular e um quadrado. Se você encontrar a área de cada um, você pode encontrar a área de toda a figura. |
|
|
|
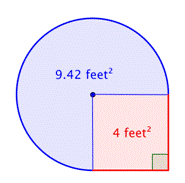
Encontrar a área do quadrado. |
|
|
|
|
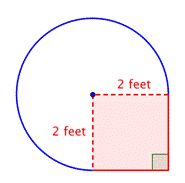
>>Localizar a área da região circular. O raio é de 2 pés. Nota que a região é |
|
|
4 pés2 + |
Adicionar as duas regiões juntas. Como a medida da área da circular é aproximada, a área da figura será também uma aproximação. |
|
Resposta |
A área é aproximadamente 13.42 pés2. |
|
Qual é a área (ao centésimo mais próximo) da figura mostrada abaixo? (Ambas as regiões arredondadas são semicírculos.)
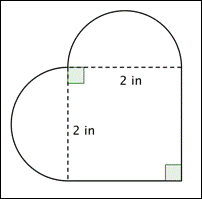
A) 16,56 in2
B) 7,14 in2
C) 4 in2
D) 3.14 in2
Sumário
Círculos são uma forma geométrica importante. A distância em torno de um círculo é chamada de circunferência, e o espaço interior de um círculo é chamado de área. O cálculo da circunferência e da área de um círculo requer um número chamado pi (![]() ), que é um decimal não terminante, não repetitivo. Pi é frequentemente aproximado pelos valores 3,14 e
), que é um decimal não terminante, não repetitivo. Pi é frequentemente aproximado pelos valores 3,14 e ![]() . Você pode encontrar o perímetro ou área de formas compostas – incluindo formas que contêm seções circulares – aplicando as fórmulas de circunferência e área quando apropriado.
. Você pode encontrar o perímetro ou área de formas compostas – incluindo formas que contêm seções circulares – aplicando as fórmulas de circunferência e área quando apropriado.