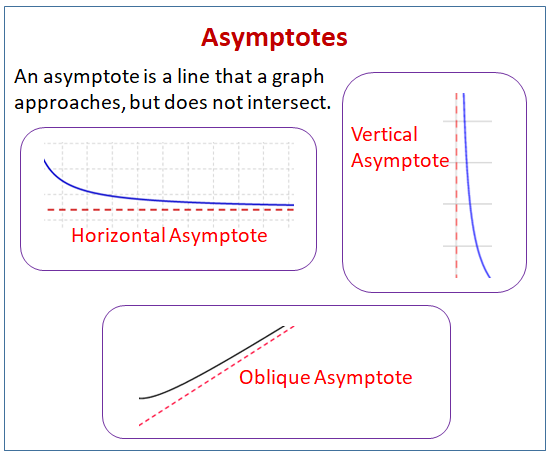
Uma assímptota é uma linha que um gráfico se aproxima, mas não se intercepta.
Nesta lição, aprenderemos como encontrar assímptotas verticais, horizontais e oblíquas (oblíquas) de funções racionais.
Tópicos relacionados:
Outras lições de Cálculo
O diagrama seguinte mostra os diferentes tipos de assímptotas: assímptotas horizontais, verticais e oblíquas. Percorra a página para mais exemplos e soluções sobre como encontrar as assímptotas.
- Como determinar a Assímptota Vertical?
- Encontrar Assímptotas Verticais de Funções Racionais
- Assímptotas Verticais de Funções Racionais: Quick Way to Find Them
- Como encontrar assímptotas verticais de funções racionais
- Como determinar a Assímptota horizontal?
- Corte para encontrar as assímptotas horizontais de funções racionais
- Assímptota oblíqua ou Assímptota oblíqua
- Localizar as assímptotas oblíquas de funções racionais
- Localizar Assímptotas de uma Função Racional (Vertical, Horizontal e Oblíqua/Inclinada)
- De encontrar todas as Assímptotas de uma Função Racional (Vertical, Horizontal, Oblíqua / oblíqua)
Como determinar a Assímptota Vertical?
Método 1: Use a Definição de Assímptota Vertical
A linha x = a é chamada de Assímptota Vertical da curva y = f(x) se pelo menos uma das seguintes afirmações for verdadeira.
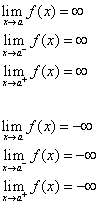
Método 2:
Para funções racionais, as assímptotas verticais são linhas verticais que correspondem aos zeros do denominador.
Dada a função racional, f(x)
Passo 1: Escreva f(x) de forma reduzida
Passo 2: se x – c é um fator no denominador então x = c é a assímptota vertical.
Exemplo:
Encontrar as assímptotas verticais de ![]()
Solução:
Método 1: Use a definição de Assímptota Vertical.
Se x é próximo de 3 mas maior que 3, então o denominador x – 3 é um pequeno número positivo e 2x é próximo de 8. Assim, ![]() é um grande número positivo.
é um grande número positivo.
Intuitivamente, vemos que
![]()
Similiarmente, se x é próximo de 3 mas menor que 3, então x – 3 é um pequeno número negativo e 2x é próximo de 8. Então, ![]() é um grande número negativo.
é um grande número negativo.
![]()
A linha x = 3 é a assímptota vertical.
Método 2:
Passo 1: f(x) já está em forma reduzida.
Passo 2: O denominador é x – 3, e assim a Assímptota Vertical está em x = 3.
Encontrar Assímptotas Verticais de Funções Racionais
O que procurar, a fim de encontrar assímptotas verticais de funções racionais.
- Mostrar Soluções Passo a Passo
Assímptotas Verticais de Funções Racionais: Quick Way to Find Them
Exemplo de encontrar assímptotas verticais de funções racionais.
- Mostrar Soluções Passo a Passo
Como encontrar assímptotas verticais de funções racionais
- Mostrar Soluções Passo a Passo
Como determinar a Assímptota horizontal?
Método 1: Use a definição de Assímptota Horizontal
A linha y = L é chamada de assímptota horizontal da curva y = f(x) se
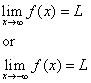
Método 2:
Para a função racional, f(x)
Se o grau de x no numerador for menor que o grau de x no denominador então y = 0 é a assímptota horizontal.
Se o grau de x no numerador for igual ao grau de x no denominador, então y = c onde c é obtido dividindo os coeficientes principais.
Exemplo:
>
Ponham as assimetrias horizontal e vertical da função.
![]()
Solução:
Método 1:
Dividir ambos numerador e denominador por x.
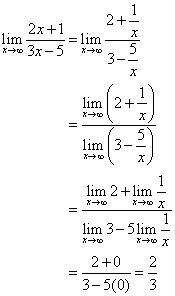
A linha ![]() é a assímptota horizontal.
é a assímptota horizontal.
Método 2:
O grau de x no numerador é igual ao grau de x no denominador.
Dividindo os coeficientes principais obtemos ![]()
A linha ![]() é a assímptota horizontal.
é a assímptota horizontal.
Corte para encontrar as assímptotas horizontais de funções racionais
Um par de truques que tornam muito fácil encontrar as assímptotas horizontais de funções racionais
- Mostrar soluções passo a passo
Este vídeo dará uma visão básica das assímptotas horizontais. Vamos determinar se as funções racionais dadas têm assímptotas horizontais e o que são.
- Mostrar Soluções Passo-a-Passo
Este vídeo irá para mais detalhes sobre as regras das assímptotas horizontais.
- Mostrar Soluções Passo-a-Passo
Assímptota oblíqua ou Assímptota oblíqua
Algumas curvas têm assímptotas que são oblíquas, isto é, nem horizontais nem verticais.
Se ![]() então a linha y = mx + b é chamada de assímptota oblíqua ou oblíqua porque as distâncias verticais entre a curva y = f(x) e a linha y = mx + b se aproximam 0,
então a linha y = mx + b é chamada de assímptota oblíqua ou oblíqua porque as distâncias verticais entre a curva y = f(x) e a linha y = mx + b se aproximam 0,
Para funções racionais, as assímptotas oblíquas ocorrem quando o grau do numerador é um a mais do que o grau do denominador. Neste caso, a equação da assímptota oblíqua pode ser encontrada por divisão longa.
Exemplo:
>
Localizar as assímptotas da função ![]()
Solução:
Desde que o denominador x2 + 1 nunca é 0, não há assímptota vertical.
Desde que o grau de x no numerador é maior que o grau de x no denominador não há assímptota horizontal.
Desde que o grau de x no numerador é um maior que o grau de x no denominador podemos usar divisão longa para obter a assímptota oblíqua.
![]()
Então, a linha y = x é a assímptota oblíqua.
Localizar as assímptotas oblíquas de funções racionais
Este vídeo descreve quando uma função racional tem uma assímptota oblíqua, descreve brevemente o que é uma assímptota oblíqua, e depois faz dois exemplos.
- Mostrar Soluções Passo a Passo
Localizar Assímptotas de uma Função Racional (Vertical, Horizontal e Oblíqua/Inclinada)
Este vídeo mostra como encontrar as assímptotas verticais e as assímptotas oblíquas/ilíquas de uma função racional.
- Mostrar Soluções Passo a Passo
De encontrar todas as Assímptotas de uma Função Racional (Vertical, Horizontal, Oblíqua / oblíqua)
Aqui se olha para uma função e se encontra a assímptota vertical e também se conclui que não existem assímptotas horizontais, mas que existe uma assímptota oblíqua. Usamos então uma divisão longa para encontrar a assímptota oblíqua.
- Mostrar soluções passo a passo
Tente a calculadora Mathway livre e o solucionador de problemas abaixo para praticar vários tópicos matemáticos. Tente os exemplos dados, ou digite seu próprio problema e verifique sua resposta com as explicações passo-a-passo. 

