O que se segue é a minha tomada de alguns problemas de matemática supostamente “common core math” ou “nova matemática” que têm circulado na Internet. Eu sinto que eles nos mostram uma implementação mal orientada do CCS.
Calma em mente, nem tudo que você vê nos livros de matemática ou na internet é feito corretamente com base no CCS. Em alguns dos exemplos que você vê, parece que as pessoas estão jogando fora o senso comum quando fazem problemas matemáticos para abordar os padrões centrais comuns!
Não estou surpreso que a implementação tenha acabado “atamancada” em alguns lugares. Os CCS são uma mudança tão grande para a maioria dos professores que eles precisam de muito apoio e reeducação antes de serem obrigados a ensinar-lhes.
Eu sempre pensei que o PRINCIPAL problema enfrentado pela educação matemática nas séries elementares nas escolas públicas é que muitos professores do ensino fundamental não entendem matemática o suficiente para serem capazes de ensiná-la corretamente, mesmo no nível elementar. Por exemplo, muitos deles não entendem os conceitos, os porquês e onde os algoritmos que ensinam. A culpa não é deles – o problema se remonta ao que lhes foi ensinado na formação de professores e em sua própria escolaridade.
O próprio documento de normas é um pouco difícil de seguir nos lugares. A sua leitura requer alguma reflexão. Eu gostaria que alguém produzisse um livreto que explicasse os padrões em linguagem simples e com numerosos exemplos.
Maus exemplos de “common core” ou “nova matemática”
Exemplo 1
Recentemente eu vi uma imagem de estratégias de subtração no Facebook, que dizia ser de um livro de matemática da 1ª série e que era “Common Core math”.”
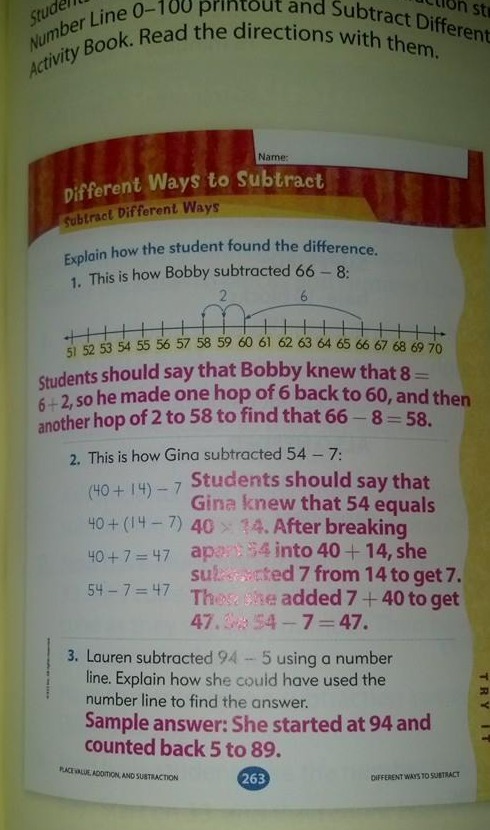
Eu acho que o método 2 é muito difícil para a 1ª série, e eu deixaria até mesmo o método 1 para a 2ª série.
No entanto, esse livro não parece estar nem alinhado com os padrões do Common Core. Os padrões para a 1ª classe simplesmente não incluem esses tipos de problemas de subtracção!
Isto é o que encontramos nos padrões:
Adicionar e subtrair dentro de 20.
1.OA.5
Contagem de adição e subtração (por exemplo, contando com 2 para adicionar 2).
1.OA.6.
Adicionar e subtrair dentro de 20, demonstrando fluência para adição e subtração dentro de 10. Usar estratégias como contar com dez (por exemplo, 8 + 6 = 8 + 2 + 4 = 10 + 4 = 14); decompondo um número levando a dez (por exemplo, 13 – 4 = 13 – 3 – 1 = 10 – 1 = 9); usando a relação entre adição e subtração (por exemplo, sabendo que 8 + 4 = 12, sabe-se que 12 – 8= 4); e criando somas equivalentes mas mais fáceis ou conhecidas (por exemplo, adicionando 6 +7 criando o equivalente conhecido 6 + 6 + 1 = 12 + 1 = 13).
O exemplo do livro de texto parece querer abordar 1.OA.6 acima, mas isso é claramente para adicionar e subtrair dentro de 20, não com números maiores.
Anterior nos padrões do 1º grau vemos dois padrões que têm a ver com a subtracção de números de dois dígitos (dentro de 100):
1.NBT.5.
Dado um número de dois dígitos, mentalmente encontre 10 a mais ou 10 a menos que o número, sem ter que contar; explique o raciocínio usado.
1.NBT.6.
Subtrair múltiplos de 10 no intervalo 10-90 de múltiplos de 10 no intervalo 10-90 (diferenças positivas ou zero), usando modelos concretos ou desenhos e estratégias baseadas no valor do local, propriedades das operações, e/ou a relação entre adição e subtração; relacionar a estratégia a um método escrito e explicar o raciocínio usado.
Nota da Maria: isto significa subtrações como 34 – 20 ou 89 – 60.
mas nenhuma destas inclui subtrações como 54 – 7 ou 82 – 6. Estas estão na 2ª classe:
2.NBT.5
Adicionar e subtrair fluentemente dentro de 100 usando estratégias baseadas em valor de lugar, propriedades de operações, e/ou a relação entre adição e subtração.
Nota que o padrão de 2ª série não especifica COMO você subtrai (se você usa estratégias mentais matemáticas ou escreve números abaixo uns dos outros e pede emprestado/regrupa).
Exemplo 2
De Houghton Mifflin, supostamente:
Juanita quer dar sacos de adesivos para seus amigos. Ela quer dar o mesmo número de autocolantes a cada amigo. Ela não tem certeza se precisa de 4 sacos ou 6 sacos de autocolantes. Quantos autocolantes poderia ela comprar para que não restem autocolantes?
O problema dos autocolantes tem a ver com o conceito do múltiplo menos comum (LCM). (A resposta é que ela deve comprar 12, 24, 36, ou qualquer outro múltiplo de 12 adesivos, pois assim ela pode dividi-los em 4 sacos ou 6 sacos)
Certo, o problema é MUITO pouco claro e mal formulado. O meu palpite é que o livreto em que isto aparece é simplesmente não editado. Não é culpa dos padrões em si. Eu concordo com Bart Goddard no Fórum de Matemática. Este é um sintoma da pressa cega de produzir problemas da “vida real” que acabam por não ser sensatos.
Do documento PDF em que ele aparece, concluo que o problema é para a quarta série, porque todas as outras palavras problemas no livreto correspondem aos padrões para a quarta série (fatores, primes). Mas, o CCS nem sequer inclui o múltiplo menos comum nos padrões da 4ª série (está na 6ª)! Alguma coisa ficou realmente fora de controle com essa palavra problema.
Exemplo 3
Again, supostamente de Houghton Mifflin para a 1ª série. Isto corresponde ao padrão que já citei acima:
Adicionar e subtrair dentro de 20.
1.OA.6.
Adicionar e subtrair dentro de 20, demonstrando fluência para adição e subtracção dentro de 10. Usar estratégias como contar com dez (por exemplo, 8 + 6 = 8 + 2 + 4 = 10 + 4 = 14); decompondo um número levando a dez (por exemplo, 13 – 4 = 13 – 3 – 1 = 10 – 1 = 9); usando a relação entre adição e subtração (por exemplo, sabendo que 8 + 4 = 12, sabe-se 12 – 8= 4); e criando somas equivalentes mas mais fáceis ou conhecidas (por exemplo, adicionando 6 + 7 criando o equivalente conhecido 6 + 6 + 1 = 12 + 1 = 13).
Agora, a estratégia de “fazer dez” tem a ver com ADICIONAR, não com subtrair. Em subtração, ela é chamada de “decomposição de um número que leva a um dez”. Então as instruções devem dizer: “O que mostra uma maneira de decompor um número que leva a um dez?”. Eu sinto que é absolutamente NONSENSE exigir que os alunos do 1º ano conheçam essa terminologia.
Mas há outro problema aqui. Se você realmente ler todos os padrões, você notará que em vários outros lugares ele pede aos alunos para explicar o raciocínio utilizado ou para relacionar um determinado método visual à estratégia, mas NÃO neste padrão!
A forma como eu vejo este padrão é que os professores devem ENSINAR as várias estratégias mencionadas e depois dar aos alunos SIMPLES problemas de adição e subtração dentro de 20 como 15 – 8 e 10 – 6. Eu NÃO vejo este padrão exigindo que os alunos reconheçam se um determinado modelo visual corresponde a uma determinada estratégia.
Again, parece que o autor joga fora o bom senso… e não entende os padrões.
Exemplo 4
O exemplo abaixo é muito mal formulado mas o CONCEITO por trás dele é muito bom e também é encontrado no Mammoth Matemático. Eu posso então descobrir o que eles querem.
Vemos cinco quadrados. Colorir um pouco de azul e o resto de vermelho. Isso é claro.
Então colorir os quadrados na “ligação numérica” da mesma forma. A ligação de números vai para esses três círculos. Uma criança que tenha estado presente em uma aula onde o professor ensina laços numéricos espera saber o que isso significa. É o mesmo conceito de uma família de fatos… o número superior é a soma ou o total (5), e os números que vão para os círculos inferiores correspondem a quantos você coloriu de azul e quantos de vermelho, neste caso 1 e 4.
Então eu acho que os parceiros ocultos também são os 1 e 4. Mostre 1 e 4 dedos a um adulto. Finalmente a cor 1 e 4 dedos na imagem (e não os seus próprios dedos como parece).
Na minha opinião a parte sobre os dedos é superflua e confusa. No entanto, o conceito de ligações numéricas é muito mais antigo do que o CCS. Ligações numéricas não são na verdade mencionadas no CCS, embora elas se liguem a este padrão:
1.OA.4
Entenda a subtração como um problema de adendo desconhecido. Por exemplo, subtraia 10 – 8 encontrando o número que faz 10 quando adicionado a 8.
e com este
1.OA.6.
Adicionar e subtrair dentro de 20, demonstrando fluência para adição e subtração dentro de 10.
Não sei porque é que esse número de folha de trabalho de ligação é dado como um exemplo de Matemática de Núcleo Comum. Seria muito melhor se fosse um exemplo de folha de trabalho de matemática mal redigida que COULD mesmo data para núcleo pré-comum (e é apenas reutilizada neste currículo em particular)… porque, como eu disse, os laços de números NÃO são mencionados no CCS.
Que padrões de matemática Common Core não são
- Não são “nova matemática”. Comparado com muitos currículos de matemática usados nos anos 2000 que enfatizavam algoritmos não tradicionais, o CCS é um claro movimento em direção aos algoritmos tradicionais e à memorização. Veja estes padrões específicos:
2.OA.2
Adicionar e subtrair com fluidez dentro de 20 usando estratégias mentais. No final do Grau 2, saiba de memória todas as somas de dois números de um dígito.
Maria’s note: estes são seus fatos básicos de adição, como 7 + 7 ou 5 + 4.3.OA.7
Fluently multiplicar e dividir dentro de 100, usando estratégias como a relação entre multiplicação e divisão (por exemplo, sabendo que 8 × 5 = 40, sabe-se 40 ÷ 5 = 8) ou propriedades de operações. Pelo endof Grau 3, conhecer de memória todos os produtos de dois números de um dígito.
Maria: isto significa tabelas de multiplicação e fatos básicos de divisão.4.NBT.4
Adicionar e subtrair com frequência números inteiros de vários dígitos usando o algoritmo padrão.5.NBT.5
Multiplicar com frequência números inteiros de vários dígitos usando o algoritmo padrão.
Nota da Maria: isto não significa que os alunos multipliquem números inteiros de vários dígitos apenas na 5ª série; isto é estudado também na 3ª e 4ª séries. - Os padrões não impõem estratégias ou modelos visuais estranhos aos professores e alunos. Muitos padrões deixam isso a cargo dos professores e dos alunos. Por exemplo:
2.NBT.5
Aumentar e subtrair com fluidez dentro de 100 usando estratégias baseadas no placevalue, propriedades de operações, e/ou a relação entre adição e subtração.Notificar o “e/ou” na frase acima. Isto significa que os professores e alunos NÃO se limitam a usar quaisquer estratégias específicas nem são aconselhados a usar várias estratégias. O tradicional algoritmo de “empréstimo” é uma estratégia baseada no valor do lugar, por isso está incluído aqui mesmo no 2.NBT.5.
2.NBT.9
Explicar porque é que as estratégias de adição e subtracção funcionam, usando o valor de lugar e as propriedades das operações. Explicações podem ser suportadas por desenhos ou objetos.Diz “pode ser suportado por desenhos” mas não o obriga a fazê-lo, nem o limita a usar um modelo visual específico ou tipo de desenho.
3.OA.3
Utilizar multiplicação e divisão dentro de 100 para resolver problemas de palavras insituação envolvendo grupos iguais, matrizes e quantidades de medidas, por exemplo, usando desenhos e equações com um símbolo para o número desconhecido representar o problema.O aluno não TEM de usar um desenho. Isso é apenas mencionado como uma possibilidade.
4.NBT.5
Multiplicar um número inteiro de até quatro dígitos por um número inteiro de um dígito, e multiplicar dois números de dois dígitos, usando estratégias baseadas no valor do lugar e nas propriedades das operações. Ilustre e explique o cálculo usando equações, matrizes retangulares e/ou areamodelos.Note o “e/ou”. Ilustre o cálculo mas é suficiente para ilustrá-lo usando equações. Você não TEM que ilustrar usando arrays.
Dito isto, alguns padrões mencionam um modelo visual específico, como um modelo de linha numérica ou de área retangular, mas isto é menos comum do que dar uma escolha como nos padrões acima.
Matemática conceitual
Existem alguns padrões que entram no lado conceitual da matemática que os professores do ensino fundamental podem não entender se não forem ensinados o que significam; por exemplo:
5. NF.7b
Interprete a divisão de um número inteiro por uma fração de unidade e calcule tais quocientes. Por exemplo, crie um contexto de história para 4 ÷ (1/5), e use um modelo de fração visual para mostrar o quociente. Use a relação entre multiplicação e divisão para explicar que 4 ÷ (1/5) = 20 porque 20 × (1/5) = 4.
Um desses problemas seria: quantas peças que têm 1/5 pés de comprimento você pode cortar de uma peça de material de 4 pés? Um modelo visual poderia mostrar 4 grossas, divididas em quintas. Podemos então contar que 4 atacados têm um total de 20 quintos.
5.NF.4b
Conheça a área de um retângulo com comprimentos laterais fracionários, colocando um quadrado com comprimentos laterais de fração unitários apropriados, e mostre que a área é a mesma que seria encontrada multiplicando os comprimentos laterais. Multiplique os comprimentos laterais fracionários para encontrar áreas de retângulos, e represente produtos fracionários como áreas retangulares.
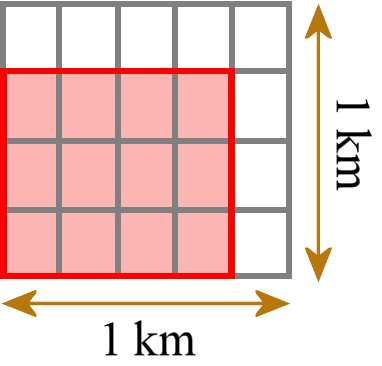Isto significa, por exemplo, um retângulo com comprimentos laterais de 3/4 km e 4/5 km. Em seguida, ladrilhamo-lo com pequenos rectângulos unitários (não quadrados unitários; aqui o próprio padrão tem a terminologia errada) que cada um tem comprimentos laterais de 1/4 km e 1/5 km.
Podemos contar quantos pequenos rectângulos precisamos. Precisamos de 12 azulejos deste tipo. Cada ladrilho tem uma área de 1/20 km2, portanto a área total é de 12/20 km2. Então verificamos e comparamos que obtemos a mesma resposta como se tivéssemos multiplicado os dois comprimentos laterais usando a multiplicação da fração regular (3/4 km × 4/5 km = 12/20 km2).
Eu sempre tive esse tipo de problema em meus livros – mesmo antes do CCS aparecer.
Algumas pessoas argumentam que as crianças não precisam de tal entendimento conceitual ou que é muito difícil. Pessoalmente, eu discordo. Sempre me esforcei (também antes da CCS) para explicar os conceitos de aritmética de fração para que os alunos não acabem “seguindo cegamente as regras”, só podendo calcular com frações se eles por acaso se lembrarem corretamente da regra. Sempre enfatizei o entendimento conceitual em matemática (como meus leitores sabem!).
Mas, espero que vocês possam ver como algumas dessas coisas podem ser desconhecidas dos professores e pais das escolas, e por isso não é de se admirar que seguir os Common Core Standards seja difícil para eles.
É minha esperança que a série Mammoth Light Blue Series e as unidades que eu vendo em minhas lojas Teachers Pay Teachers e Teachers’ Notebook possam ajudar os professores & pais que precisam de materiais alinhados ao Common Core. E como eu disse, o resto de vocês pode estar confiante em usá-los também. Eles não contêm nenhuma matemática “estranha” ou sem sentido, mas como sempre, baseiam-se simplesmente na sólida base do ensino dos conceitos de matemática juntamente com os procedimentos.
Por Maria Miller