
Galileo é frequentemente considerado o pai da ciência moderna. Foi ele quem reuniu os princípios da experiência, teoria e matemática em um quadro padrão. Provavelmente, mais do que qualquer outro Galileu foi a pessoa responsável pelo desenvolvimento da ciência moderna.
Dizia que Galileu deixou cair duas bolas de aço de massas diferentes, mas o mesmo material da torre inclinada de Pisa e elas pousaram ao mesmo tempo. O que é notável sobre este experimento é que ele lançou um novo método de fazer ciência onde você conduz um experimento para testar uma hipótese. Ele mostrou que temos que fazer mais do que apenas pensar que algo é verdade, mas também temos que provar isso.

Galileo encontrou um paradoxo interessante enquanto era chefe do Departamento de Matemática da Universidade de Pisa.
Definição: Um paradoxo, também conhecido como antinomia, é uma afirmação logicamente auto-contraditória ou uma afirmação que vai contra a expectativa de alguém. (Wikipédia). (Grego: “para” = além, “doxa” = crença)
O paradoxo de Galileo era determinar se dois conjuntos contendo objetos infinitos são equivalentes um ao outro. Por exemplo, deixe P é o conjunto de inteiros positivos onde P= {0,1,2,3,…} e E é o conjunto de números pares onde E = {0,2,4,6,…}. Galileu alegou que os tamanhos destes dois conjuntos serão os mesmos porque podemos emparelhar cada número inteiro positivo do conjunto P com os números pares do conjunto E.

Então, como é que o tamanho dos dois conjuntos é o mesmo quando um número “menor” aparece em E? Isso foi chamado de paradoxo de Galileu e iniciou um novo debate sobre o conceito de infinito.
Após Galileu, seu estudante Evangelista Torricelli tornou-se chefe do Departamento de Matemática da Universidade de Pisa. Talvez o tenha ouvido devido aos seus trabalhos sobre pressão atmosférica e à invenção do barômetro. Como Toricelli também está interessado em matemática, ele pergunta:
É possível ter um objeto com um volume finito e uma superfície infinita? Em primeiro lugar, tal coisa parece improvável para a maioria de nós. No entanto, a matemática nos diz que tal coisa poderia acontecer. Torricelli respondeu a sua própria pergunta e descobriu o Trompete de Toricelli cuja superfície é infinita, mas cujo volume é finito. A sua descoberta vista como um paradoxo “incrível”.
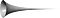
A propósito, há uma regra essencial na filosofia matemática; Seja qual for a época da filosofia ou da matemática com que se lida, ela está relacionada com a história, a cultura e a religião daquela região. É por isso que eles chamam a trombeta de Toricelli também de Trompa de Gabriel. Uma referência aqui é feita à Bíblia porque os cristãos acreditam que o anjo, Gabriel, tocará a trompa no Dia do Julgamento.
Então como se forma a trompa de Toricelli? Todos nós sabemos como se faz o gráfico y=x. Se você grafar a equação y=1/x onde x é maior ou igual a 1, o gráfico será assim:
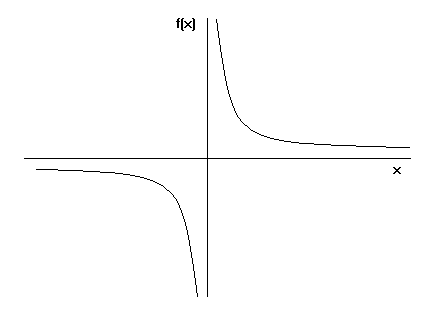
Quando pegamos o gráfico de y=1/x e o giramos em torno do eixo x, vemos a trombeta de Toricelli.

Felizmente, temos fórmulas matemáticas em nossas mãos para calcular a área e o volume da trombeta de Toricelli. Quando usamos a fórmula de integração abaixo para o volume da trompete, obtemos uma quantidade finita.
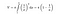
No entanto, quando aplicamos a fórmula de integração para a área de superfície da trompete, desta vez, a área de superfície da mesma torna-se infinita. Este resultado não é interessante?
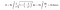
>Desde que o volume da trombeta de Toricelli seja finito, podemos enchê-la com uma quantidade finita de tinta. Por exemplo, vamos supor que o volume dela é de 100 litros. Eu vou ao Home Depot e compro 100 litros de tinta e encho-o. No entanto, o que torna isto interessante é que terei pintado a superfície infinita com esses 100 litros de tinta. Hoje, a maioria das pessoas chama este paradoxo, “o paradoxo do pintor”
Houston, temos aqui um problema! A situação que é impossível na prática torna-se possível na matemática. Então, como pode a trombeta do Torricelli ser real? Ou, como podemos precisamente combinar todos os elementos dos conjuntos enquanto um dos conjuntos é um subconjunto de outro no exemplo de Galileu?
A razão de todos estes conflitos é que o conceito de infinito não é semelhante a outros conceitos que conhecemos, e isso confunde muitas pessoas. Galileu diz pelo seu paradoxo,
“Sim, meu amigo, existe o infinito. É inútil opor-se a ele. Os conjuntos em que estou trabalhando são exemplos de conjuntos fechados que envolvem o infinito. Eles começam em um ponto e vão até o infinito, e mesmo assim, eles ainda estão definidos. Entretanto, meus comentários e conceitos sobre o infinito devem ser diferentes daqueles que eu usaria para as magnitudes finitas. Se você está lidando com magnitudes finitas, você pode dizer que 3 quilos são menos de 5 quilos, ou 32 metros é mais longo que 7 metros. Mas quando se trata de infinito, você não pode dizer que esse infinito é maior, menor ou igual a isso.”
Foi a solução de Galileu 1600s.
Felizmente, a solução de Galileu tinha iniciado um novo debate sobre o infinito. Os matemáticos e filósofos não conseguiram chegar a acordo sobre uma resposta específica até que Cantor compartilhou sua “teoria do conjunto”, que os alunos aprendem hoje na escola elementar.
Podemos historiar periodicamente o desenvolvimento da idéia do infinito. Ela surgiu da Eleatics, que foi uma escola de filosofia pré-Socrática fundada por Parmenides no início do século V a.C., na antiga cidade de Elea. Havia três grandes filósofos nesta escola, tais como Zeno, Xenófanes e Parmênides. Nesta escola, a filosofia aceita era a de que a existência era singular, e não havia pluralidade. Zeno era famoso por seus paradoxos no infinito nos Eleatics. Mais tarde, nos anos 300 a.C., Aristóteles surgiu e propôs um par de conceitos para explicar os paradoxos de Zeno, que eram infinito potencial e infinito real.
O infinito potencial é um grupo de números ou grupo de “coisas” que continua sem terminar, continuar ou repetir-se vezes sem conta, sem ponto final reconhecível.
O infinito real envolve conjuntos sem fim ou “coisas” dentro de um espaço que tem início e fim; é uma série que é tecnicamente “concluída” mas que consiste num número infinito de membros.
Aristóteles acreditava que não havia um infinito real. Esta idéia de Aristóteles dominou o mundo da filosofia até os anos 1600. Então filósofos como Cusa e Bruno afirmaram que existe o infinito real, mas não podemos dar sentido a ele. Depois de Cuso e Bruno, o grande pensador Spinoza juntou-se ao assunto.
Spinoza disse que nós podíamos entender o conceito de infinito e classificá-los em tamanho. No entanto, ele também afirmou que não conseguia fazer as contas sobre eles. Por exemplo, ele poderia adicionar 3 a 5, mas não poderia adicionar um infinito a outro.
Finalmente, para terminar esses debates, um belo homem, Georg Cantor apareceu e encontrou a teoria do conjunto, que ainda é a base da matemática. Ele fixou o ponto final nas discussões do infinito com sua teoria do set.
Ele nos mostrou que um set infinito seria maior ou menor que outro set infinito. Além disso, Cantor alegou que poderíamos adicionar e multiplicar conjuntos de infinito. Até então, os humanos tinham seguido as idéias de Aristóteles sobre o infinito. De acordo com Aristóteles, se multiplicarmos o número 3 pelo infinito, ele seria infinito novamente. O infinito engoliria tudo. Com base nisso, ele afirmou que haveria apenas infinito potencial, não infinito real.
No entanto, Cantor nos provou o oposto da idéia de Aristóteles com a teoria do conjunto. Se adicionarmos um a um conjunto infinito, não será mais o mesmo conjunto. Ele tentou comparar os infinitos. Por exemplo, Cantor provou que o conjunto de todas as funções de (0,1)→ℕ é contável. Assim ele definiu um para um e para a função do intervalo (0,1) para números naturais.
Em outras palavras, ele provou que números totalmente naturais podem caber entre 0 e 1 porque havia números racionais infinitos entre 0-1, e esses infinitos podem ser pareados. Então ele fez algo ainda mais perigoso do que encontrar dois infinitos iguais. Ele comparou o infinito dos números reais com o infinito dos números naturais e descobriu que o infinito dos números reais é maior do que o outro. Ele até olhou para sua prova e disse a seu amigo Dedekind: “Eu vejo, mas nem eu posso acreditar…”.
Cantor também era um matemático com preocupações filosóficas e religiosas muito sérias. Ao desenvolver a teoria do set, ele disse: “Deus me ditou a teoria do set”.
A teoria do set não foi amplamente aceita quando ela foi desenvolvida pela primeira vez. As empresas nem sequer contrataram Cantor para qualquer trabalho. Um matemático, Henri Poincaré, disse uma vez: “As ideias deste Cantor são uma doença má que se agarra ao colarinho da matemática”. E a matemática vai tratá-lo um dia”. Cantor teve que ir a um hospital psiquiátrico por um tempo e morreu lá. Mas hoje, nós o consideramos um gênio.
Cantor era um homem solitário no limite do infinito. Ele citou a Bíblia no início do seu artigo sobre Números Transfinitas: “Tudo o que está escondido será trazido à luz.”