>
A identidade de Euler parece desconcertante:
>
![]() >
>
Sai de uma fórmula mais geral:
![]() >
>
>
Yowza — estamos relacionando um expoente imaginário com seno e cosseno! E de alguma forma ligando o pi dá -1? Isto poderia ser intuitivo?
Não segundo o matemático de 1800 Benjamin Peirce:
É absolutamente paradoxal; não podemos entendê-lo, e não sabemos o que significa, mas já o provamos, e por isso sabemos que deve ser a verdade.
Argh, esta atitude faz o meu sangue ferver! As fórmulas não são feitiços mágicos a serem memorizados: devemos, devemos, devemos, devemos encontrar um insight. Aqui está a minha:
A fórmula do elogiador descreve duas formas equivalentes de se mover em círculo.
É isso? Esta espantosa equação é sobre girar em volta? Sim — e podemos entendê-la construindo algumas analogias:
- Iniciando no número 1, veja a multiplicação como uma transformação que muda o número: $1 \cdot e^{i \pi}$
- Crescimento exponencial regular aumenta continuamente 1 por alguma taxa durante algum período de tempo; crescimento exponencial imaginário aumenta continuamente 1 por algum tempo
- Crescimento para unidades de tempo “pi” significa ir radiante pi em torno de um círculo
- Por isso, $e^{i \pi}$ significa começar em 1 e rodar pi (a meio de um círculo) para chegar a -1
Esta é a vista de alto nível, vamos mergulhar nos detalhes. A propósito, se alguém tentar impressioná-lo com $e^{i \pi} = -1$, pergunte a eles sobre i ao i-ésimo poder. Se eles não conseguem pensar bem, a fórmula de Euler ainda é um feitiço mágico para eles.
Atualizar: Enquanto escrevo, achei que um vídeo poderia ajudar a explicar as idéias mais claramente:
Entendendo cos(x) + i * sin(x)
O sinal de igual está sobrecarregado. Algumas vezes queremos dizer “definir uma coisa para outra” (como x = 3) e outras queremos dizer “estas duas coisas descrevem o mesmo conceito” (como $\sqrt{-1} = i$).
A fórmula de Euler é a última: dá duas fórmulas que explicam como mover-se em círculo. Se examinarmos o movimento circular usando trigonometria, e viajar x radianos:
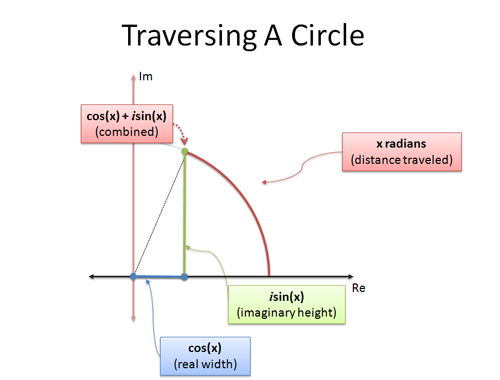
- cos(x) é a coordenada x (distância horizontal)
- sin(x) é a coordenada y (distância vertical)
A afirmação
![]()
é uma forma inteligente de esmagar as coordenadas x e y num único número. A analogia “números complexos são bidimensionais” nos ajuda a interpretar um único número complexo como uma posição em um círculo.
Quando definimos x como $\pi$, estamos viajando $\pi$ unidades ao longo do exterior do círculo de unidades. Porque a circunferência total é $2\pi$, o velho $\pi$ está a meio caminho, colocando-nos a -1,
Neato: O lado direito da fórmula de Euler ($\cos(x) + i \sin(x)$) descreve o movimento circular com números imaginários. Agora vamos descobrir como o lado e da equação o realiza.
O que é Crescimento Imaginário?
Combinar coordenadas x- e y- num número complexo é complicado, mas manejável. Mas o que é que um expoente imaginário significa?
Vamos dar um passo atrás. Quando vejo $3^4$, penso assim:
- 3 é o resultado final de crescer instantaneamente (usando e) a uma taxa de ln(3). Em outras palavras: $3 = e^{\ln(3)}$
- $3^4$ é o mesmo que crescer até 3, mas depois crescer por 4x o mesmo tempo. Então $3^4 = e^{\ln(3) {\cdot 4} = 81$
Em vez de ver os números por si mesmos, você pode pensar neles como algo que e teve que “crescer para”. Números reais, como 3, dão uma taxa de juros de ln(3) = 1,1, e é isso que e “recolhe” à medida que vai crescendo, crescendo continuamente.
O crescimento regular é simples: continua “empurrando” um número na mesma, real direção em que estava indo. 3 × 3 empurra na direção original, tornando-o 3 vezes maior (9).
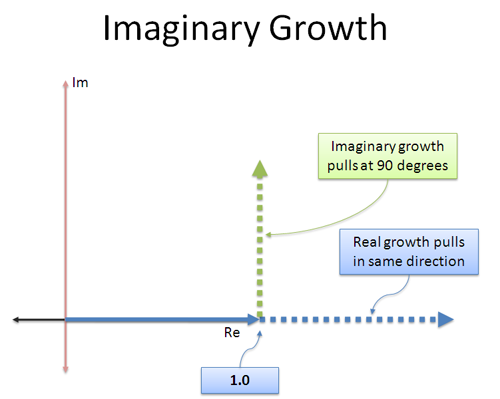
Crescimento mágico é diferente: o “interesse” que ganhamos está em uma direção diferente! É como um motor a jacto que estava amarrado de lado — em vez de avançarmos, começamos a empurrar a 90 graus.
>
O que é mais arrumado num empurrão ortogonal constante (perpendicular) é que não te acelera nem te abranda — faz-te girar! Tomando qualquer número e multiplicando por i não vai mudar sua magnitude, apenas a direção que ele aponta.
Intuitivamente, aqui está como eu vejo a taxa de crescimento imaginário contínuo: “Quando eu crescer, não me empurres para a frente ou para trás na direcção em que já estou a ir. Gire-me em vez disso”.
Mas não deveríamos girar mais rápido e mais rápido?
Eu também me perguntei isso. Compostos de crescimento regular na nossa direção original, então vamos 1, 2, 4, 8, 16, multiplicando 2x cada vez e ficando nos números reais. Podemos considerar este $e^{\ln(2)x}$, que significa crescer instantaneamente a uma taxa de ln(2) por “x” segundos.
E hey — se a nossa taxa de crescimento fosse duas vezes mais rápida, 2ln(2) vs ln(2), pareceria o mesmo que crescer por duas vezes mais tempo (2x vs x). A magia do e nos permite trocar taxa e tempo; 2 segundos em ln(2) é o mesmo crescimento de 1 segundo em 2ln(2).
Agora, imagine que temos uma taxa de crescimento puramente imaginária (Ri) que nos faz girar até atingirmos i, ou 90 graus para cima. O que acontece se dobrarmos essa taxa para 2Ri, vamos girar fora do círculo?
Nope! Ter uma taxa de 2Ri significa que apenas giramos o dobro da velocidade, ou alternativamente, giramos a uma taxa de R durante o dobro do tempo, mas vamos ficar no círculo. Rodar o dobro do tempo significa que agora estamos enfrentando 180 graus.
Após percebermos que alguma taxa de crescimento exponencial pode nos levar de 1 a i, aumentando essa taxa só nos faz girar mais. Nunca escaparemos do círculo.
No entanto, se a nossa taxa de crescimento é complexa (a+bi vs Ri) então a parte real (a) irá nos fazer crescer como normal, enquanto a parte imaginária (bi) nos faz girar. Mas não vamos ficar extravagantes: A fórmula de Euler, $e^{ix}$, é sobre o crescimento puramente imaginário que nos mantém no círculo (mais tarde).
>
A Quick Sanity Check
>
Enquanto escrevo, tive de esclarecer algumas questões para mim:
Porquê usar $e^x$, não estamos a rodar o número 1?
e representa o processo de começar em 1 e crescer continuamente a 100% de interesse por 1 unidade de tempo.
Quando escrevemos e estamos capturando todo esse processo em um único número — e representa todo o rigmarole de crescimento contínuo. Então realmente, $e^x$ está dizendo “comece em 1 e cresça continuamente a 100% por x segundos”, e começa de 1 como nós queremos.
Mas o que eu como expoente faço?
Para um expoente regular como $3^4$ perguntamos:
- Qual é a taxa de crescimento implícita? Estamos crescendo de 1 a 3 (a base do expoente).
- Como podemos mudar essa taxa de crescimento? Nós escalamos por 4x (o poder do expoente).
Nós podemos converter nosso crescimento em formato “e”: nossa taxa instantânea é ln(3), e nós a aumentamos para ln(3) * 4. Novamente, o poder do expoente (4) apenas escalou nossa taxa de crescimento.
![]()
Quando o expoente superior é i (como em $3^i$), nós apenas multiplicamos nossa taxa de crescimento implícita por i. Então ao invés de crescer em ln(3), estamos crescendo em ln(3) * i.
![]()
A parte superior do expoente modifica a taxa de crescimento implícito da parte inferior.
Pormenores da granulometria de nitrogênio
Vejamos mais de perto. Lembre-se desta definição de e:
Que $\frac{100\%}{n}$ representa a porção de juros que ganhamos em cada período microscópico. Assumimos que a taxa de juros era de 100% na dimensão real — mas e se fosse 100% na direção imaginária?
![]()
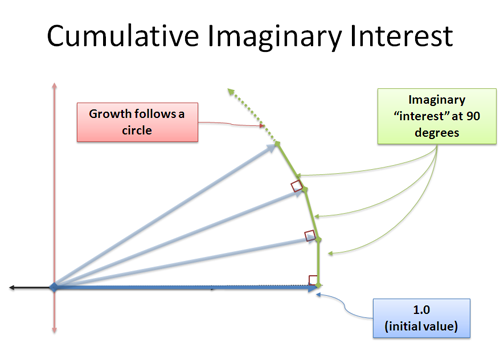
Agora, nossos juros recém-formados se somam a nós na direção dos 90 graus. Surpreendentemente, isto não muda o nosso comprimento — este é um conceito complicado, porque parece fazer um triângulo onde a hipotenusa deve ser maior. Estamos lidando com um limite, e a distância extra está dentro da margem de erro que especificamos. Isto é algo que eu quero resolver em outro dia, mas acredite na minha palavra: o crescimento perpendicular contínuo irá girar você. Este é o coração do seno e do coseno, onde sua mudança é perpendicular à sua posição atual, e você se move em um círculo.
Aplicamos i unidades de crescimento em incrementos infinitamente pequenos, cada um nos empurrando em um ângulo de 90 graus. Não existe uma rotação “cada vez mais rápida” – em vez disso, rastejamos ao longo do perímetro uma distância de |i| = 1 (magnitude de i).
E hey — a distância rastejada ao redor de um círculo é um ângulo em radianos! Encontramos outra maneira de descrever o movimento circular!
Para obter o movimento circular: Mude continuamente girando em ângulo de 90 graus (também conhecido como taxa de crescimento imaginário).
Então, a fórmula de Euler diz “crescimento exponencial, imaginário traça um círculo”. E este caminho é o mesmo que mover-se num círculo usando seno e cosseno no plano imaginário.
Neste caso, a palavra “exponencial” é confusa porque viajamos em torno do círculo a uma velocidade constante. Na maioria das discussões, supõe-se que o crescimento exponencial tem um efeito cumulativo e composto.
alguns exemplos
Você realmente não acredita em mim, acredita? Aqui estão alguns exemplos, e como pensar neles intuitivamente.
Exemplo: $e^i$
Onde está o x? Ah, é apenas 1. Intuitivamente, sem quebrar uma calculadora, sabemos que isso significa “viajar 1 radiano ao longo do círculo da unidade”. Na minha cabeça, eu vejo “e” tentando crescer 1 a 100% na mesma direção, mas eu continuo movendo a bola e forço “1” a crescer ao longo da borda de um círculo:
![]()
Não é o número mais bonito, mas lá está ele. Lembre-se de colocar sua calculadora em modo radiano ao perfurar isto em.
Exemplo: $3^i$
Isso é complicado — não está em nosso formato padrão. Mas lembre-se, ![]()
Queremos um crescimento inicial de 3x no final do período, ou uma taxa instantânea de ln(3). Mas, o i aparece e muda essa taxa de ln(3) para “i * ln(3)”:
Pensamos que iríamos nos transformar a uma taxa regular de ln(3), um pouco mais rápida que 100% de crescimento contínuo já que e é cerca de 2,718. Mas oh não, eu girei: agora estamos nos transformando a uma taxa imaginária, o que significa que estamos apenas girando em torno. Se eu fosse um número regular como 4, ter-nos-ia feito crescer 4x mais rápido. Agora estamos crescendo a uma velocidade de ln(3), mas de lado.
Devemos esperar um número complexo no círculo unitário — não há nada na taxa de crescimento para aumentar nosso tamanho. Resolvendo a equação:
![]()
Então, ao invés de terminarmos em “1” unidade ao redor do círculo (como $e^i$) acabamos em ln(3) unidades ao redor.
Exemplo: $i^i$
A poucos meses atrás, isto ter-me-ia feito chorar. Hoje não! Vamos quebrar as transformações:
![]() >
>
Comecemos com 1 e queremos mudá-lo. Como resolver $3^i$, qual é a taxa de crescimento instantâneo representada por i como base?
Hrm. Normalmente faríamos ln(x) para obter a taxa de crescimento necessária para atingir x no final de 1 unidade de tempo. Mas para uma taxa imaginária? Precisamos de fazer uma macarronada.
Para começar com 1 e crescer até i precisamos de começar a rodar no início. A que velocidade? Bem, precisamos de obter 90 graus (pi/2 radianos) em 1 unidade de tempo. Então nossa taxa é $i {\pi}{\pi}{\pi}{\pi}{\pi}{\pi}{\pi}{\pi} Lembre-se que a nossa taxa deve ser imaginária já que estamos a rodar, não a crescer! O velho e simples $2$ é cerca de 1,57 e resulta em crescimento regular.
Isto deve fazer sentido: para girar 1,0 para i no final de 1 unidade, devemos girar $2$ radianos (90 graus) nessa quantidade de tempo. Então, para obter “i” podemos usar $e^{i \frac{\pi}{2}}$.
>![]() >
>
Phew. Isso descreve o “i” como a base. Que tal o expoente?
Bem, o outro i diz-nos para mudarmos a nossa taxa — sim, essa taxa que passámos tanto tempo a descobrir! Então ao invés de girarmos a uma velocidade de $i \frac{\pi}{\i}{\i}{\i}$, que é o que uma base de i significa, transformamos a taxa para:
>![]() >
>
O i’s cancela e torna a taxa de crescimento real novamente! Giramos a nossa taxa e nos empurramos para os números negativos. E uma taxa de crescimento negativa significa que estamos encolhendo — devemos esperar $i^i$ para fazer as coisas menores. E faz:
![]()
Tada! (Pesquise “i^i” no Google para usar sua calculadora)
>
Pega um respirador: Você pode intuitivamente descobrir como as bases imaginárias e expoentes imaginários devem se comportar. Whoa.
E como bônus, você descobriu ln(i) — para fazer $e^x$ tornar-se i, fazer e girar $\frac{\pi}{2}$ radians.
![]()
Exemplo: (i^i)^i
Um expoente imaginário duplo? Se você insiste. Primeiro, sabemos qual será a nossa taxa de crescimento dentro dos parênteses:
![]()
Obtém-se uma taxa de crescimento negativa (encolhimento) de -pi/2. E agora modificamos essa taxa novamente por i:
![]()
E agora temos uma rotação negativa! Vamos dar a volta ao círculo a uma taxa de $–\frac{\pi}{\i}{\i}{\i1}$ por unidade de tempo. Por quanto tempo vamos? Bem, há uma unidade implícita de tempo “1” no topo desta cadeia exponencial; o padrão implícito é ir por 1 unidade de tempo (assim como $e = e^1$). 1 unidade de tempo nos dá uma rotação de $-\frac{\pi}{2}$ radianos (-90 graus) ou -i!
>
![]()
E, só por chutes, se nós quadrássemos esse resultado maluco:
![]()
É “só” o dobro da rotação: 2 é um número regular então duplica nossa taxa de rotação para um total de -180 graus em uma unidade de tempo. Ou, você pode olhar para ele como aplicando -90 graus de rotação duas vezes seguidas.
No primeiro blush, estes são expoentes realmente estranhos. Mas com as nossas analogias podemos tomá-los em passos.
Crescimento Complexo
Podemos ter um crescimento real e imaginário ao mesmo tempo: a porção real nos escalona, e a parte imaginária nos faz girar:
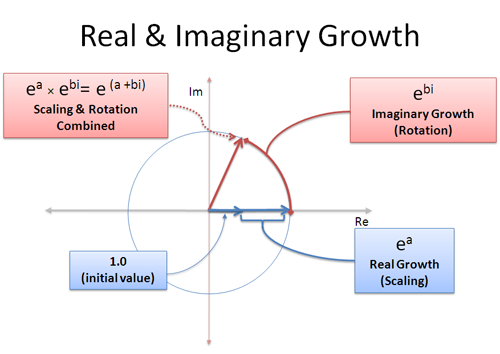
Uma taxa de crescimento complexa como (a + bi) é uma mistura de crescimento real e imaginário. A parte real a, significa “crescer a 100% por um segundo” e a parte imaginária b significa “girar por b segundos”. Lembre-se, as rotações não obtêm o benefício da composição já que você continua “empurrando” em uma direção diferente — a rotação soma linearmente.
Com isto em mente, podemos representar qualquer ponto em qualquer círculo de tamanho usando (a+bi)! O raio é $e^a$ e o ângulo é determinado por $e^{bi}$. É como colocar o número no expand-o-tron por dois ciclos: uma vez para aumentá-lo no tamanho certo (a segundos), outra vez para girá-lo para o ângulo certo (b segundos). Ou, você poderia girá-lo primeiro e depois crescer!
Vamos dizer que queremos saber a quantidade de crescimento para chegar a 6 + 8i. Isto é realmente pedir o log natural de um número imaginário: como crescemos e para chegar a (6 + 8i)?
- Radius: De que tamanho de um círculo precisamos? Bem, a magnitude é $\sqrt{6^2 + 8^2} = \sqrt{100} = 10$. O que significa que precisamos crescer por ln(10) = 2,3 segundos para atingir essa quantidade.
- Montante para girar: Qual é o ângulo desse ponto? Podemos usar o arctan para descobrir: atan(8/6) = 53 graus = .93 radian.
- Combinar o resultado: ln(6+8i) = 2.3 + .93i
Isto é, podemos alcançar o ponto aleatório (6 + 8i) se usarmos $e^{2.3 + .93i}$.
Por que é que isto é útil?
A fórmula do elogiador dá-nos outra forma de descrever o movimento num círculo. Mas já poderíamos fazer isso com seno e coseno — o que é tão especial?
É tudo uma questão de perspectiva. Seno e cosseno descrevem o movimento em termos de uma grelha, traçando coordenadas horizontais e verticais.

A fórmula do elenco usa coordenadas polares — qual é o seu ângulo e distância? Mais uma vez, são duas formas de descrever o movimento:
- Sistema de grelha: Vá 3 unidades para leste e 4 unidades para norte
- Coordenadas polares: Vá 5 unidades num ângulo de 53,13 graus
Dependente do problema, as coordenadas polares ou rectangulares são mais úteis. A fórmula de Euler nos permite converter entre as duas para usar a melhor ferramenta para o trabalho. Também, porque $e^{ix}$ pode ser convertido para seno e coseno, podemos reescrever fórmulas em trigonometria como variações em e, que vem em muito útil (não é preciso memorizar sin(a+b), você pode derivar isso — mais um dia). E é lindo que cada número, real ou complexo, é uma variação de e.
Mas utilidade, schmutility: o resultado mais importante é a realização de que equações desconcertantes podem se tornar intuitivas com as analogias certas. Não deixe belas equações como a fórmula de Euler permanecerem um feitiço mágico — construa sobre as analogias que você conhece para ver os insights dentro da equação.
Feliz matemática.
Apendice
O screencast foi divertido, e o feedback é definitivamente bem-vindo. Acho que ajuda as idéias a estourar, e caminhar pelo artigo me ajudou a encontrar lacunas na minha intuição.
- Brian Slesinsky tem uma apresentação clara sobre a fórmula de Euler.
- Análise Complexa Visual tem uma grande discussão sobre a fórmula de Euler — veja a p. 10 na Pré-Visualização do Google Book
- Fiz uma palestra sobre Matemática e Analogias que explica a Identidade de Euler de forma mais visual:
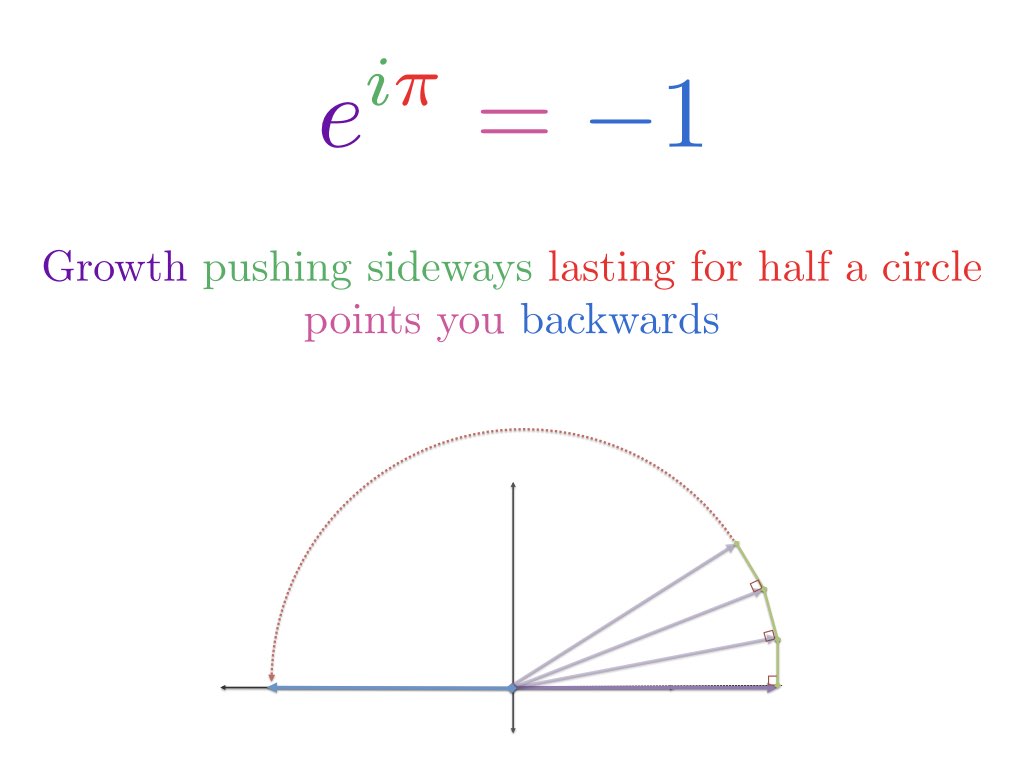
Outros Posts Nesta Série
- Um Guia Visual, Intuitivo de Números Imaginários
- Aritmética Intuitiva Com Números Complexos
- Entendendo Porque Funciona a Multiplicação Complexa
- Guia Intuitiva de Números Imaginários, Graus e Radianos
- Entendimento intuitivo da fórmula de Euler
- Um guia interativo para a transformação de Fourier
- Guia intuitiva para a convolução
- Entendimento intuitivo das ondas sinusoidais
- Um guia intuitivo da álgebra linear
- Uma intuição do programador para multiplicação de matriz
- Multiplicação imaginária vs. Exponentes Imaginários
>
>
>
>