Imagine um quadrado de papel deitado sobre a sua secretária. Peço-lhe que feche os olhos. Você ouve o deslocamento do papel. Quando você abre os olhos, o papel não parece ter mudado. O que eu poderia ter feito enquanto você não estava olhando?
É óbvio que eu não girei o papel em 30 graus, porque então o papel ficaria diferente.

Eu também não o virei através de uma linha conectando, digamos, um dos cantos ao ponto médio de outra borda. O papel ficaria diferente se eu tivesse.

O que eu poderia ter feito, no entanto, era rodar o papel no sentido horário ou anti-horário por qualquer múltiplo de 90 graus, ou virá-lo através de uma das linhas diagonais ou das linhas horizontais e verticais.
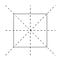
Uma forma útil de visualizar as transformações é marcar os cantos do quadrado.

A última opção é não fazer nada. Isto é chamado de transformação de identidade. Juntas, estas são todas chamadas de transformações de simetria do quadrado.
Eu posso combinar transformações de simetria para fazer outras transformações de simetria. Por exemplo, duas voltas através do segmento de linha BD produzem a identidade, assim como quatro rotações sucessivas de 90 graus no sentido contrário ao dos ponteiros do relógio. Uma inversão sobre a linha vertical seguida de uma inversão sobre a linha horizontal tem o efeito seguro como uma rotação de 180 graus. Em geral, qualquer combinação de transformações de simetria produzirá uma transformação de simetria. A tabela seguinte dá as regras para compor transformações de simetria:

Nesta tabela, R com subscritos 90, 180 e 270 denotam rotações no sentido anti-horário de 90, 180 e 270 graus, H significa uma inversão sobre a linha horizontal, V é uma inversão sobre a linha vertical, MD é uma inversão sobre a diagonal de cima para baixo à esquerda e OD significa uma inversão sobre a outra diagonal. Para encontrar o produto de A e B, vá para a linha de A e depois para a coluna de B. Por exemplo, H∘MD=R₉₀.
Existem algumas coisas que você pode notar olhando para a tabela:
- A operação ∘ é associativa, significando que A∘(B∘C) = (A∘B)∘C para qualquer transformação A, B, e C.
- Para qualquer par de transformações de simetria A e B, a composição A∘B é também uma transformação de simetria
- Há um elemento e tal que A∘e=e∘A para cada transformação de simetria A
- Para cada transformação de simetria A, existe uma única transformação de simetria A-¹ tal que A∘A-¹=A-¹∘A=e
Dizemos portanto que o conjunto das transformações de simetria de um quadrado, combinado com a composição, forma uma estrutura matemática chamada grupo. Este grupo é chamado D₄, o grupo dietético para o quadrado. Estas estruturas são o assunto deste artigo.
Definição de um grupo
Um grupo ⟨G,*⟩ é um conjunto G com uma regra * para combinar quaisquer dois elementos em G que satisfaçam os axiomas do grupo:
No abstrato muitas vezes suprimimos * e escrevemos a*b como ab e nos referimos a * como multiplicação.

Não é necessário que * seja comutativo, significando que a*b=b*a. Você pode ver isto olhando a tabela de D₄, onde H∘MD=R₉₀ mas MD∘H=R₂₇₀. Grupos onde * é comutativo são chamados de grupos abelianos após Neils Abel.
Gruposbelianos são a exceção e não a regra. Outro exemplo de um grupo não-abeliano são as transformações de simetria de um cubo. Considere apenas rotações sobre os eixos:
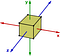
Se eu rodar primeiro 90 graus no sentido anti-horário em torno do eixo y e depois 90 graus no sentido anti-horário em torno do eixo z, então o seu resultado será diferente do que se eu rodar 90 graus em torno do eixo z e depois 90 graus em torno do eixo y.

É possível que um elemento seja o seu próprio inverso. Considere o grupo que consiste de 0 e 1 com a operação de adição binária. Sua tabela é:

Claramente 1 é o seu próprio inverso. Este também é um grupo abeliano. Não se preocupe, a maioria dos grupos não são tão chatos.
Alguns outros exemplos de grupos incluem:
- O conjunto de inteiros com adição.
- O conjunto de números racionais sem incluir 0 com multiplicação.
- O conjunto de soluções para a equação polinomial xⁿ-1=0, chamada de enésima raiz da unidade, com multiplicação.
Aqui estão alguns exemplos que não são grupos:
- O conjunto de números naturais sob adição não é um grupo porque não há inversos, que seriam os números negativos.
- O conjunto de todos os números racionais incluindo 0 com multiplicação não é um grupo porque não existe um número racional q para o qual 0/q=1, portanto nem todos os elementos têm um inverso.
Estrutura do grupo
Um grupo é muito mais do que apenas um blob que satisfaz os quatro axiomas. Um grupo pode ter uma estrutura interna, e esta estrutura pode ser muito complexa. Um dos problemas básicos em álgebra abstrata é determinar como é a estrutura interna de um grupo, já que no mundo real os grupos que são realmente estudados são muito maiores e mais complicados do que os simples exemplos que demos aqui.
Um dos tipos básicos de estrutura interna é um subgrupo. Um grupo G tem um subgrupo H quando H é um subconjunto de G e:
- Para a,b∈H, a*b∈H e b*a∈H
- Para a∈H, a-¹∈H
- A identidade é um elemento de H
Se H≠G então H é dito que é um subgrupo próprio. O subgrupo de G constituído apenas pela identidade é chamado de subgrupo trivial.
Um grupo não-eleitoral pode ter subgrupos comutativos. Considere o grupo da catedral quadrada que discutimos na introdução. Este grupo não é abeliano mas o subgrupo de rotações é abeliano e cíclico:
Damos agora dois exemplos de estrutura de grupo.
Even se um grupo G não é abeliano, ainda pode ser que haja uma coleção de elementos de G que se deslocam com tudo em G. Esta coleção é chamada de centro de G. O centro C é um subgrupo de G. Proof:
Agora suponha que f é uma função cujo domínio e alcance são ambos G. Um período de f é um elemento a∈G tal que f(x)=f(ax) para todos x∈G. O conjunto P de períodos de f é um subgrupo de G. Proof:
Grupos finitos são finitamente gerados
Vimos que os grupos cíclicos são gerados por um único elemento. Quando é possível escrever cada elemento de um grupo G como produtos de um subconjunto A de G (não necessariamente próprio), então dizemos que A gera G e escrevemos isto como G=⟨A⟩. A prova mais “bem, duh” que você já verá é a prova de que todos os grupos finitos são gerados por um conjunto gerador finito:
- Let G ser finito. Cada elemento de G é um produto de dois outros elementos de G então G=⟨G⟩. QED.
 >
>
>
>
Acabaremos este artigo com uma aplicação.
Comunicação resistente aos erros
>
A forma mais simples de transmitir informação digital é codificá-la em cordas binárias de comprimento fixo. Nenhum esquema de comunicação está completamente livre de interferências, portanto há sempre a possibilidade de que os dados errados sejam recebidos. O método de decodificação de máxima probabilidade é uma abordagem simples e eficaz para detectar e corrigir erros de transmissão.
Deixe 𝔹ⁿ ser o conjunto de cadeias binárias, ou palavras, de comprimento, n. É simples mostrar que 𝔹ⁿ é um grupo abeliano sob adição binária sem carregar (de modo que, por exemplo, 010+011=001). Note que cada elemento é o seu próprio inverso. Um código C é um subconjunto de 𝔹ⁿ. O seguinte é um exemplo de um código em 𝔹⁶:
C = {000000, 001011, 010110, 011101, 100101, 101110, 110011, 111000}
Os elementos de um código são chamados de codewords. Somente as codewords serão transmitidas. Diz-se que ocorre um erro quando a interferência muda um pouco em uma palavra transmitida. A distância d(a,b) entre duas codewords a e b é o número de dígitos em que duas codewords diferem. A distância mínima de um código é a menor distância entre quaisquer duas de suas codewords. Para o código de exemplo logo acima, a distância mínima é três.
No método de decodificação de probabilidade máxima, se recebermos uma palavra x, que pode conter erros, o receptor deve interpretar x como a palavra de código a tal que d(a,x) seja um mínimo. Vou mostrar que para um código de distância mínima m isto pode sempre (1) detectar erros que mudam menos de m bits e (2) corrigir erros que mudam ½(m-1) ou menos bits.

No nosso código de exemplo, m=3 e a esfera de raio ½(m-1)=1 sobre a palavra de código 011101 é {011101, 111101, 001101, 011001, 010101, 011111, 011111, 011100}. Então se o receptor recebe alguma destas palavras, ele sabe que deveria receber 011101.
Então tudo bem, mas o que é que isso tem a ver com teoria de grupo? A resposta está em como nós realmente produzimos os códigos com os quais este método funciona.
É possível que um código em 𝔹ⁿ forme um subgrupo. Neste caso, dizemos que o código é um código de grupo. Códigos de grupo são grupos finitos, portanto são finitamente gerados. Veremos como produzir um código encontrando um grupo gerador.
Um código pode ser especificado para que os primeiros bits de cada palavra de código sejam chamados de bits de informação e os bits no final sejam chamados de bits de paridade. No nosso exemplo de código C, os três primeiros bits são de informação e os três últimos são de paridade. Os bits de paridade satisfazem as equações de verificação de paridade. Para um código A₁A₂A₃A₄A₅A₆ as equações de paridade são A₄=A₁+A₂, A₅=A₂+A₃, e A₆=A₁+A₃. As equações de paridade fornecem outra camada de proteção contra erros: se alguma das equações de paridade não estiver satisfeita, então ocorreu um erro.
Aqui está o que fazemos. Suponha que queremos codewords com m bits de informação e n bits de paridade. Para gerar um código de grupo, escreva uma matriz com m linhas e m+n colunas. No bloco formado pelas primeiras m colunas, escreva a matriz com m×m de identidade. Na coluna j para m+1≤j≤m_n, escreva 1 na kth row se Aₖ aparecer na equação de paridade para o bit de paridade Aⱼ e 0 caso contrário. No nosso código de exemplo, a matriz é:

Tal matriz é chamada de matriz geradora para o código do grupo. Você pode verificar diretamente que as linhas geram C:

As linhas de qualquer matriz geradora formam um conjunto gerador para um código de grupo C. Prova:
- Identidade e inversos: Qualquer linha adicionada a si mesma dá a identidade, uma string composta por todos os zeros.
- Closure: Se A,B∈C então A e B são somas de linhas da matriz geradora então A+B é também uma soma de linhas da matriz geradora. Portanto A+B∈C.
Isto nos permite gerar um código, agora vou mostrar como gerar um código útil.
Definir o peso w(x) para significar o número de linhas em x. Por exemplo, w(100101)=3. É óbvio que w(x)=d(x,0) onde 0 é uma palavra cujos dígitos são todos zeros. O peso mínimo W de um código é o peso da palavra de código não zero com o menor número de algarismos do código. Para um código de distância mínima m, d(x,0)≥m então w(x)≥m e portanto W=m.
Recorde que para uma palavra ser considerada como palavra de código, ela deve satisfazer um conjunto de equações de verificação de paridade. Para o nosso código de exemplo, estas são A₄=A₁+A₂, A₅=A₂+A₃, e A₆=A₁+A₃. Podemos também escrevê-las como um sistema linear:
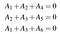
Que por si só pode ser escrito em termos de produtos ponto:

Or de forma mais compacta como Ha=0 onde a=(A₁,A₂,A₃,A₄,A₅,A₆) e H é a matriz de verificação de paridade para o código:

Pode-se verificar por cálculo directo que se w(a)≤2 então não podemos ter Ha=0. Em geral, o peso mínimo é t+1 onde t é o menor número, tal como qualquer coleção de colunas t de H não somam a zero (ou seja, elas são linearmente independentes). Provar isso nos levaria um pouco longe demais na álgebra linear.
Se isso te assusta, não te preocupes. Podemos produzir alguns códigos muito bons sem isso, aproveitando o facto de que o resultado que acabei de mencionar implica que se cada coluna de H é diferente de zero e não há duas colunas iguais, então o peso mínimo, e portanto a distância mínima do código, é de pelo menos três. Isto é muito bom: se se espera que nosso sistema de comunicação tenha um erro de bit para cada cem palavras transmitidas, então apenas uma em cada dez mil palavras transmitidas terá um erro não corrigido e uma em um milhão de palavras transmitidas terá um erro não detectado.
Então agora temos uma receita para produzir um código útil para o esquema de detecção de probabilidade máxima para codewords contendo m bits de informação e n bits de paridade:
- Criar uma matriz com m+n colunas e n linhas. Preencha a matriz com uns e zeros para que não haja duas colunas iguais e nenhuma coluna seja apenas zeros.
- Cada linha da matriz de verificação de paridade resultante corresponde a uma das equações de paridade de bits. Escreva-as como um sistema de equações e resolva-as de modo que cada bit de paridade seja escrito em termos dos bits de informação.
- Criar uma matriz com colunas m+n e m linhas. No bloco formado pelas primeiras colunas m, escreva a matriz de identidade m×m. Na coluna j para m+1≤j≤m_n, escreva 1 na linha kth se Aₖ aparecer na equação de paridade para o bit Aⱼ e 0 caso contrário.
- As linhas desta matriz são os geradores de um grupo de códigos com distância mínima de três. Este é o código que vamos usar.
Como exemplo, suponha que eu preciso de um código simples, de oito palavras e só preciso de alguma detecção básica de erros e não correção, para que eu possa escapar com uma distância mínima de dois. Eu quero três bits de informação e dois bits de paridade. Escrevo a seguinte matriz de verificação de paridade:
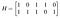
Existem dois pares de colunas que são iguais, portanto o menor t para o qual qualquer coleção de colunas t é linearmente independente é um, portanto o peso mínimo, e portanto a distância mínima que terei, é dois. As linhas representam as equações de verificação de paridade A₄=A₁+A₃ e A₅=A₁+A₂+A₃. Minha matriz geradora é portanto:

E as linhas desta matriz geram o grupo de códigos:
- {00000, 00111, 01001, 01110, 10011, 10100, 111010, 11101}
Comentários de fecho
Álgebra abstrata é um assunto profundo com implicações de longo alcance, mas também é muito fácil de aprender. Além de algumas referências passageiras à álgebra linear, quase tudo o que discuti aqui é acessível a alguém que só teve álgebra do ensino médio.
Quando tive a idéia de escrever este artigo, eu realmente queria falar sobre o cubo de Rubik, mas no final eu queria escolher um exemplo que pudesse ser coberto apenas com as idéias mais básicas da teoria de grupo. Além disso, há tanto a dizer sobre o grupo do cubo de Rubik que ele merece uma peça isolada, de modo que isso virá em breve.
Os meus cursos universitários em álgebra abstrata foram baseados no livro A Book of Abstract Algebra de Charles Pinter, que é e tratamento acessível. Os exemplos neste artigo foram todos emprestados com alguma modificação de Pinter.
Como nota final, quaisquer imagens que não sejam citadas são meu próprio trabalho original e podem ser usadas com atribuição. Como sempre, agradeço quaisquer correcções ou pedidos de esclarecimento.