Valor Eigenal

Álgebra > Álgebra Linear > Matrizes > Valores Eigenais Matrix >
>

Álgebra > Álgebra Linear > Matrizes > Decomposição Matricial >

Os valores próprios são um conjunto especial de escalares associados a um sistema linear de equações (i.e., uma equação matricial) que às vezes são também conhecidas como raízes características, valores característicos (Hoffman e Kunze 1971), valores próprios, ou raízes latentes (Marcus e Minc 1988, p. 144).

A determinação dos autovalores e autovectores de um sistema é extremamente importante em física e engenharia, onde é equivalente à diagonalização matricial e surge em aplicações tão comuns como a análise de estabilidade, a física de corpos rotativos, e pequenas oscilações de sistemas vibratórios, para citar apenas algumas. Cada autovalor é emparelhado com um autovector correspondente (ou, em geral, um autovector direito correspondente e um autovector esquerdo correspondente; não há distinção análoga entre esquerdo e direito para os autovalores).

A decomposição de uma matriz quadrada em autovalores e autovectores é conhecida neste trabalho como decomposição própria, e o facto desta decomposição ser sempre possível desde que a matriz constituída pelos autovectores de seja quadrada é conhecida como o teorema da decomposição própria.

O algoritmo Lanczos é um algoritmo para calcular os valores próprios e os vectores próprios para grandes matrizes esparsas simétricas.

Deixe ser uma transformação linear representada por uma matriz . Se há um vector tal que

(1)

para algum escalar , então é chamado o autovalor de com autovector correspondente (à direita) .

Letar ser um matriz quadrada

(2)

com autovalor , então os autovectores correspondentes satisfazem

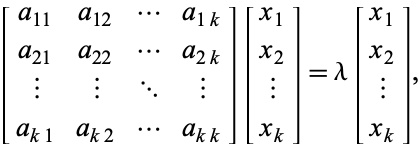(3)

o que é equivalente ao sistema homogéneo

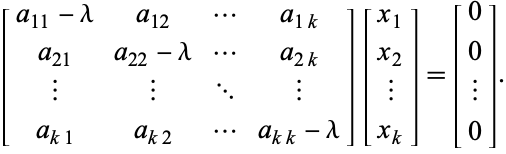(4)

Equação (4) pode ser escrita compactamente como

(5)

>onde é a matriz de identidade. Como mostrado na regra de Cramer, um sistema linear de equações tem soluções não triviais se o determinante desaparece, Assim as soluções da equação (5) são dadas por

(6)

Esta equação é conhecida como a equação característica de , e o lado esquerdo é conhecido como o polinómio característico.

Por exemplo, para uma matriz de , os valores próprios são

(7)

que surge como as soluções do caracterização

(8)

Se todos os autovalores forem diferentes, então ligando estes de volta dá equações independentes para os componentes de cada autovector correspondente, e diz-se que o sistema não é degenerado. Se os autovalores são -degenerar, então o sistema é dito ser degenerado e os autovectores não são linearmente independentes. Em tais casos, a restrição adicional de que os auto-vectores sejam ortogonais,

(9)

onde é o delta Kronecker, pode ser aplicado para render restrições adicionais, permitindo assim a solução para os auto-vectores.

Eigenvalues podem ser computados na linguagem Wolfram usando Eigenvalues. Os auto-valores e auto-valores podem ser retornados juntos usando o comando Eigensystem.

Suma que sabemos o autovalor para