Tanulási célok
- A sav vagy bázis erőssége és az \(K_a\), \(K_b\), \(pK_a\) és \(pK_b\) nagysága közötti kapcsolat ismerete.
- A kiegyenlítő hatás megértése.
Az ionizációs reakció egyensúlyi állandójának nagysága felhasználható a savak és bázisok relatív erősségének meghatározására. Például egy gyenge sav vízben történő ionizációjának általános egyenlete, ahol HA az anyasav és A- a konjugált bázisa, a következő:
\
Az egyensúlyi állandó erre a disszociációra a következő:
\}{} \label{16.5.2}\]
Mint korábban megjegyeztük, a víz koncentrációja lényegében állandó minden reakció esetében a vizes oldatban, így az \(\) egyenletben szereplő \(\ref{16.5.2}\)-t egy új mennyiségbe, a savionizációs állandóba (\(K_a\)), más néven a sav disszociációs állandójába lehet beépíteni:
\=\dfrac{}{}{} \label{16.5.3}\]
A K és \(K_a\) számszerű értékei tehát a víz koncentrációjával (55,3 M) különböznek. Az egyszerűség kedvéért \(H_3O^+\) az \(\ref{16.5.3}\) egyenletben \(H^+\) alakban írható fel. Ne feledjük azonban, hogy szabad \(H^+\) nem létezik a vizes oldatokban, és hogy minden savas ionizációs reakcióban egy proton átkerül az \(H_2O\)-ra, és hidróniumionok, \(H_3O^+\) keletkeznek. Minél nagyobb a \(K_a\), annál erősebb a sav és annál nagyobb az \(H^+\) koncentrációja az egyensúlyi állapotban. Mint minden egyensúlyi állandót, a sav-bázis ionizációs állandókat is az \(H^+\) vagy \(OH^-\) aktivitásában mérik, így egység nélküliek. A \(K_a\) értékeit számos gyakori savra vonatkozóan a \(\PageIndex{1}\) táblázat tartalmazza.
A gyenge bázisok vízzel reagálva hidroxidiont termelnek, amint azt a következő általános egyenlet mutatja, ahol B az anyabázis és BH+ a konjugált sav:
\
A reakció egyensúlyi állandója a bázis ionizációs állandója (Kb), más néven a bázis disszociációs állandója:
\= \frac{}{}{} \label{16.5.5}\]
A víz koncentrációja ismét állandó, ezért nem jelenik meg az egyensúlyi állandó kifejezésében, hanem a \(K_b\) tartalmazza. Minél nagyobb az \(K_b\), annál erősebb a bázis és annál nagyobb az \(OH^-\) koncentráció az egyensúlyi állapotban. Az \(K_b\) értékeit számos gyakori gyenge bázisra vonatkozóan a \(\PageIndex{2}\) táblázat tartalmazza.
Egy sav \(K_a\) és a konjugált bázis \(K_b\) nagysága között egyszerű kapcsolat van. Vegyük például a ciánhidrogén-sav (\(HCN\)) ionizációját vízben, hogy savas oldat keletkezzen, és \(CN^-\) reakcióját vízzel, hogy bázikus oldat keletkezzen:
\
\
A HCN ionizációjára vonatkozó egyensúlyi állandó kifejezése a következő:
\}{} \label{16.5.8}\]
A cianid vízzel való reakciójára vonatkozó megfelelő kifejezés a következő:
\}{}{} \label{16.5.9}\]
Ha az \(\ref{16.5.6}\) és \(\ref{16.5.7}\\), a következőket kapjuk:
| Reakció | Egyensúlyi állandók |
|---|---|
| \(\cancel{HCN_{(aq)}} \rightleftharpoons H^+_{(aq)}+\cancel{CN^-_{(aq)}} \) | \(K_a=\cancel{}/\cancel{}\) |
| \(\cancel{CN^-_{(aq)}}+H_2O_{(l)}+H_2O_(l)} \rightleftharpoons OH^-_{(aq)}+\cancel{HCN_{(aq)}}\) | \(K_b=\cancel{}/\cancel{}\) |
| \(H_2O_{(l)} \rightleftharpoons H^+_{(aq)}+OH^-_{(aq)}\) | \(K=K_a \times K_b=\) |
Ez esetben, az \(K_a\) és \(K_b\) által leírt reakciók összege a víz autoionizációjának egyenlete, és a két egyensúlyi állandó szorzata \(K_w\):
\
Ha tehát ismerjük egy sav \(K_a\) értékét vagy a konjugált bázis \(K_b\) értékét, akkor bármely konjugált sav-bázis párra kiszámíthatjuk a másik egyensúlyi állandót.
Az \(pH\), \(pOH\) és pKw értékekhez hasonlóan negatív logaritmusokat használhatunk, hogy elkerüljük az exponenciális jelölést a savak és bázisok ionizációs állandóinak leírásakor, ha az \(pK_a\) értéket a következőképpen határozzuk meg:
\
\
és \(pK_b\)
\
\
Hasonlóképpen, az \(\ref{16.5.10}\\), amely az \(K_a\) és \(K_b\) közötti kapcsolatot fejezi ki, logaritmikus formában a következőképpen írható fel:
\
25 °C-on ez
\
Az \(pK_a\) és \(pK_b\) értékeit számos gyakori sav és bázis esetében az \(\PageIndex{1}\) és \(\PageIndex{2}\) táblázatok tartalmazzák, illetve az E1. és E2. táblázatokban találhatók bővebb adatok. A negatív logaritmusok használata miatt az \(pK_a\) kisebb értékei nagyobb savi ionizációs állandóknak és ezáltal erősebb savaknak felelnek meg. Például a salétromsav (\(HNO_2\)), amelynek \(pK_a\) értéke 3,25, körülbelül egymilliószor erősebb sav, mint a 9,21 \(pK_a\) értékű ciánsav (HCN). Ezzel szemben az \(pK_b\) kisebb értékei nagyobb bázisionizációs állandóknak és ezáltal erősebb bázisoknak felelnek meg.
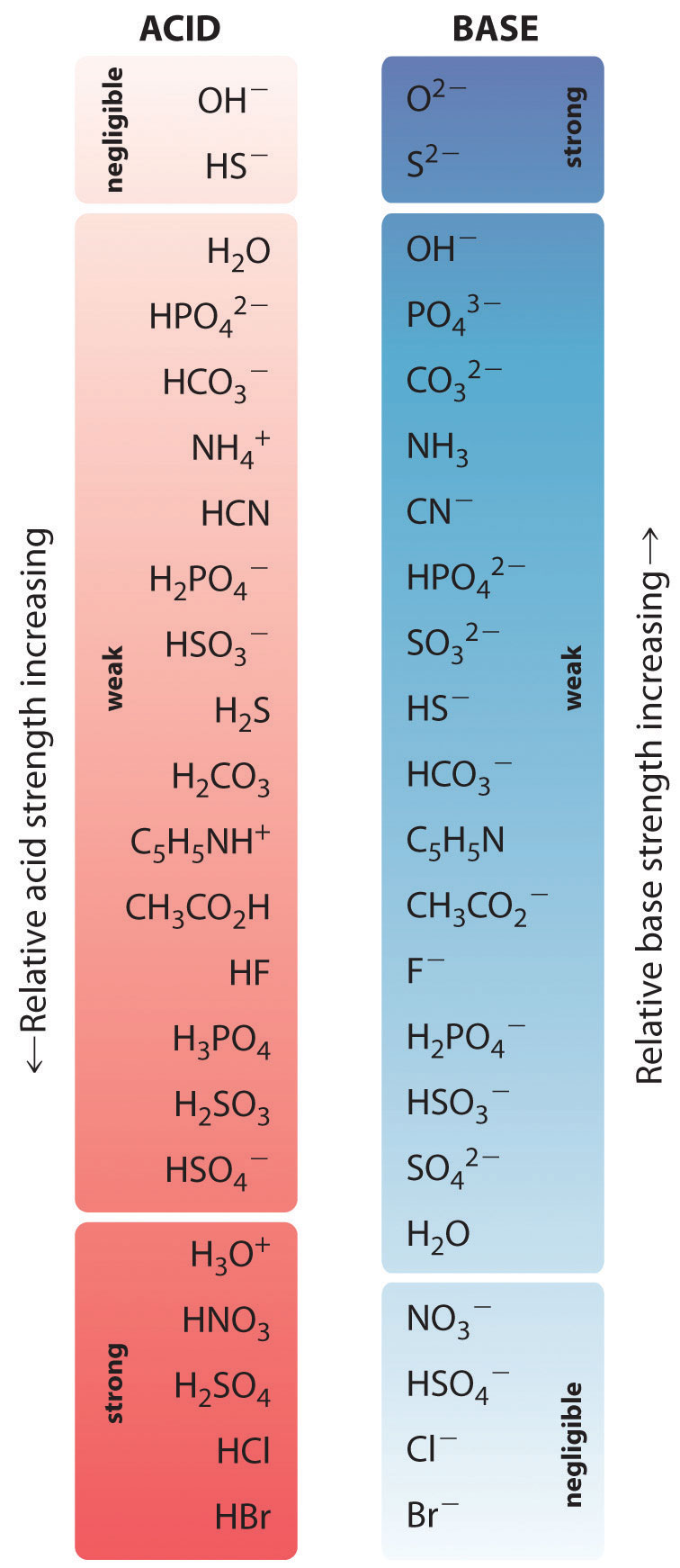
A \(\PageIndex{1}\) ábra néhány gyakori sav és konjugált bázisuk relatív erősségét mutatja be grafikusan. A konjugált sav-bázis párokat a növekvő saverősség sorrendjében (fentről lefelé) soroljuk fel, ami megfelel a \(pK_a\) csökkenő értékeinek. Ez a sorrend megfelel a konjugált bázis csökkenő erősségének vagy a \(pK_b\) növekvő értékeinek. Az \(\PageIndex{2}\) ábra bal alsó részén a leggyakoribb erős savak, jobb felső részén a leggyakoribb erős bázisok találhatók. Vegyük észre a fordított kapcsolatot az anyasav erőssége és a konjugált bázis erőssége között. Így egy erős sav konjugált bázisa egy nagyon gyenge bázis, és egy nagyon gyenge sav konjugált bázisa egy erős bázis.
Az erős sav konjugált bázisa egy gyenge bázis és fordítva.
A savak és bázisok relatív erősségét felhasználhatjuk egy sav-bázis reakció irányának előrejelzésére egyetlen szabályt követve: a sav-bázis egyensúly mindig a gyengébb savval és bázissal rendelkező oldalnak kedvez, amint azt ezek a nyilak jelzik:
\
A sav-bázis reakcióban a proton mindig az erősebb bázissal reagál.
A sósav például erős sav, amely híg vizes oldatban lényegében teljesen ionizálódik, és \(H_3O^+\) és \(Cl^-\) keletkezik; csak elhanyagolható mennyiségű \(HCl\) molekula marad disszociálatlanul. Ezért az ionizációs egyensúly gyakorlatilag teljesen jobbra fekszik, ahogyan azt egyetlen nyíl ábrázolja:
\
Az ecetsav ezzel szemben gyenge sav, a víz pedig gyenge bázis. Következésképpen az ecetsav vizes oldatai többnyire ecetsavmolekulákat tartalmaznak egyensúlyban kis koncentrációjú \(H_3O^+\) és acetátionokkal, és az ionizációs egyensúly messze balra van, amint azt ezek a nyilak ábrázolják:
\\
Hasonlóképpen, az ammónia vízzel való reakciójában a hidroxidion erős bázis, az ammónia pedig gyenge bázis, míg az ammóniumion erősebb sav, mint a víz. Ezért ez az egyensúly is balra esik:
\
Minden sav-bázis egyensúly a gyengébb savval és bázissal rendelkező oldalnak kedvez. A proton tehát az erősebb bázishoz kötődik.
Példa \(\PageIndex{1}\): Butirát és dimetil-ammóniumionok
- Kalkulálja ki a butirátion (\(CH_3CH_2CH_2CO_2^-\)) \(K_b\) és \(pK_b\) értékét. A vajsav \(pK_a\) értéke 25 °C-on 4,83. A vajsav felelős az avas vaj bűzös szagáért.
- Kalkulálja ki a dimetil-ammóniumion (\((CH_3)_2NH_2^+\)) \(K_a\) és \(pK_a\) értékét. A dimetil-amin (\((CH_3)_2NH\)) bázisionizációs állandója \(K_b\) 25°C-on \(5,4 \szer 10^{-4}\).
Adott: \(pK_a\) és \(K_b\)
Kérdés: megfelelő \(K_b\) és \(pK_b\), \(K_a\) és \(pK_a\)
Stratégia:
Az \(K_a\) és \(K_b\) állandók az \(\ref{16.5.10}\). Egy sav és konjugált bázisa \(pK_a\) és \(pK_b\) állandói az \(\ref{16.5.15}\) és \(\ref{16.5.16}\) egyenletek szerint kapcsolódnak egymáshoz. A pK = -log K és K = 10-pK összefüggések (\(\ref{16.5.11}\) és \(\ref{16.5.13}\) egyenletek) segítségével alakítsuk át a \(K_a\) és \(pK_a\) vagy \(K_b\) és \(pK_b\) értékeket.
Megoldás:
Megadjuk a vajsav \(pK_a\) értékét, és kérjük, hogy számítsuk ki a konjugált bázis, a butirátion \(K_b\) és \(pK_b\) értékét. Mivel a megadott \(pK_a\) érték 25°C-os hőmérsékletre vonatkozik, használhatjuk az \(\ref{16.5.16}\) egyenletet: \(pK_a\) + \(pK_b\) = pKw = 14,00. A \(pK_a\) helyettesítésével és a \(pK_b\) megoldásával,
\
\
Mivel \(pK_b = -\log K_b\), \(K_b\) \(10^{-9.17} = 6.8 \szor 10^{-10}\).
Ez esetben egy bázis (dimetil-amin) \(K_b\) értékét kapjuk, és azt kérjük, hogy számítsuk ki \(K_a\) és \(pK_a\) értékét a konjugált savra, a dimetil-ammóniumionra. Mivel a megadott kiindulási mennyiség \(K_b\) és nem \(pK_b\), az \(\ref{16.5.10}\) egyenletet használhatjuk: \(K_aK_b = K_w\). A \(K_b\) és \(K_w\) 25°C-on mért értékeit behelyettesítve és az \(K_a\) értékét megoldva,
\
\
Mivel \(pK_a\) = -log \(K_a\), \(pK_a = -\log(1.9 \szor 10^{-11}) = 10.72\). Ugyanezt a választ kapjuk, ha \(K_b\) átváltjuk \(pK_b\)-re:
\
\
\
\
Ha e négy mennyiség közül bármelyiket megkapjuk egy sav vagy bázis esetében (\(K_a\), \(pK_a\), \(K_b\) vagy \(pK_b\)), akkor a másik hármat ki tudjuk számítani.
gyakorlat \(\PageIndex{1}\): A tejsav (\(CH_3CH(OH)CO_2H\)) felelős a savanyú tej csípős ízéért és szagáért; úgy gondolják, hogy a fáradt izmokban fájdalmat is okoz. Az \(pK_a\) értéke 3,86 25°C-on. Számítsa ki a tejsav \(K_a\) értékét és a laktátion \(pK_b\) és \(K_b\) értékét.
Válasz
- \(K_a = 1,4 \szer 10^{-4}\) a tejsavra;
- \(pK_b\) = 10.14 és
- \(K_b = 7.2 \times 10^{-11}\) a laktátionra
Solutions of Strong Acids and Bases: A kiegyenlítő hatás
Az \(\PageIndex{1}\) táblázatban észrevehetjük, hogy az olyan savak, mint a \(H_2SO_4\) és \(HNO_3\) a hidróniumion felett helyezkednek el, ami azt jelenti, hogy \(pK_a\) értékük kisebb nullánál és erősebb savak, mint a \(H_3O^+\) ion. Emlékezzünk vissza a 4. fejezetből, hogy a savas proton gyakorlatilag minden oxosavban az oxoanion egyik oxigénatomjához kötődik. Így a salétromsavat helyesen \(HONO_2\)-ként kell írni. Sajnos azonban az oxosavak képleteit szinte mindig úgy írják, hogy a hidrogén a bal oldalon, az oxigén pedig a jobb oldalon van, így \(HNO_3\). Valójában mind a hat gyakori erős sav, amelyekkel először a 4. fejezetben találkoztunk, \(pK_a\) értéke kisebb, mint nulla, ami azt jelenti, hogy hajlamosabbak a protonvesztésre, mint a \(H_3O^+\) ion. Ezzel szemben ezen erős savak konjugált bázisai gyengébb bázisok, mint a víz. Következésképpen ezeknek az erős savaknak a protonátadási egyensúlya messze jobbra esik, és bármelyik gyakori erős sav vízhez adása a sav és a víz lényegében sztöchiometrikus reakcióját eredményezi a \(H_3O^+\) ion és a sav konjugált bázisának oldata képződésével.
Bár a \(K_a\) a \(HI\) esetében körülbelül 108-zal nagyobb, mint a \(K_a\) a \(HNO_3\) esetében, akár a \(HI\), akár a \(HNO_3\) reakciója vízzel lényegében sztöchiometrikus \(H_3O^+\) és I- vagy \(NO_3^-\) oldatot eredményez. Valójában bármely erős sav 0,1 M-os vizes oldata valójában 0,1 M \(H_3O^+\)-t tartalmaz, függetlenül az erős sav azonosságától. Ezt a jelenséget nevezzük kiegyenlítő hatásnak: bármely faj, amely erősebb sav, mint a víz konjugált sava (\(H_3O^+\)), a vizes oldatban az \(H_3O^+\) erősségére kiegyenlítődik, mivel az \(H_3O^+\) a legerősebb sav, amely a vízzel egyensúlyban létezhet. Következésképpen nem lehet különbséget tenni az olyan savak, mint a HI és a HNO3 erősségei között vizes oldatban, és alternatív megközelítést kell alkalmazni a relatív saverősségük meghatározására.
Az egyik módszer egy oldószer, például vízmentes ecetsav használata. Mivel az ecetsav erősebb sav, mint a víz, ezért gyengébb bázisnak is kell lennie, és kevésbé hajlamos egy proton befogadására, mint a \(H_2O\). A HI és a \(HNO_3\) ecetsavban lévő 0,1 M-os oldatainak vezetőképességének mérése azt mutatja, hogy a HI teljesen disszociál, de a \(HNO_3\) csak részben disszociál, és ebben az oldószerben gyenge savként viselkedik. Ez az eredmény egyértelműen azt mutatja, hogy a HI erősebb sav, mint az \(HNO_3\). A savak erősségének relatív sorrendjét és a \(K_a\) és \(pK_a\) közelítő értékeit a \(\(\PageIndex{1}\) táblázat tetején található erős savak esetében ilyen mérések és különböző nem vizes oldószerek segítségével határoztuk meg.
Vizes oldatokban a \(H_3O^+\) a legerősebb sav és a \(OH^-\) a legerősebb bázis, amely egyensúlyban létezhet a \(H_2O\)-val.
A kiegyenlítő hatás az erős bázisok oldataira is érvényes: Vizes oldatban minden OH-nál erősebb bázis az OH- erősségére nivellálódik, mert az OH- a legerősebb bázis, amely a vízzel egyensúlyban létezhet. Az olyan sók, mint a \(K_2O\), \(NaOCH_3\) (nátrium-metoxid) és \(NaNH_2\) (nátriumamid vagy nátriumamid), amelyek anionjai olyan fajok konjugált bázisai, amelyek a \(\(\PageIndex{2}\) táblázatban a víz alatt helyezkednének el, mind olyan erős bázisok, amelyek lényegében teljesen (és gyakran hevesen) reagálnak a vízzel, egy protont felvéve, \(OH^-\) és a megfelelő kation oldatát adva:
\
\
\
Más példák, amelyekkel találkozhatsz, a kálium-hidrid (\(KH\)) és a fémorganikus vegyületek, például a metil-lítium (\(CH_3Li\)).
Poliprotikus savak és bázisok
Amint tanultad, a poliprotikus savak, mint például a \(H_2SO_4\), \(H_3PO_4\) és \(H_2CO_3\) egynél több ionizálható protont tartalmaznak, és a protonok fokozatosan vesznek el. A teljesen protonált faj mindig a legerősebb sav, mivel egy semleges molekulából könnyebb egy protont eltávolítani, mint egy negatív töltésű ionból. Így a sav erőssége csökken a további protonok elvesztésével, és ennek megfelelően nő a \(pK_a\). Vegyük például a \(H_2SO_4\) reakciót:
\
Az első reakcióban az egyensúly messze jobbra van, ami megfelel annak, hogy a \(H_2SO_4\) erős sav. Ezzel szemben a második reakcióban mind a \(HSO_4^-\), mind a \(SO_4^{2-}\) jelentős mennyiségben van jelen az egyensúlyban.
Egy poliprotikus sav esetében a saverősség csökken és a \(pK_a\) nő az egyes protonok egymást követő elvesztésével.
A hidrogén-szulfátion (\(HSO_4^{2-\)) egyszerre a \(H_2SO_4\) konjugált bázisa és a \(SO_4^{2-}\) konjugált sava. A HSO4- tehát a vízhez hasonlóan savként vagy bázisként viselkedhet, attól függően, hogy a másik reakciópartner erősebb sav vagy erősebb bázis. Ezzel szemben a szulfátion (\(SO_4^{2-}\)) egy poliprotikus bázis, amely képes két protont lépcsőzetesen felvenni:
\
\
Mint bármely más konjugált sav-bázis pár, a konjugált savak és bázisok erősségei a \(pK_a\) + \(pK_b\) = pKw kapcsolattal függnek össze. Vegyük például a \(HSO_4^-/ SO_4^{2-}\) konjugált sav-bázis párost. A \(\PageIndex{1}\) táblázatból láthatjuk, hogy a \(HSO_4^-\) \(pK_a\) értéke 1,99. Ezért az \(SO_4^{2-}\) \(pK_b\) értéke 14,00 – 1,99 = 12,01. A szulfát tehát meglehetősen gyenge bázis, míg az \(OH^-\) erős bázis, így az \(\ref{16.6}\) egyenletben látható egyensúly balra esik. A \(HSO_4^-\) ion szintén nagyon gyenge bázis (\(H_2SO_4^-) \(pK_a\) = 2,0, \(HSO_4^- \(pK_b\) = 14 – (-2,0) = 16\)), ami megfelel annak, amit egy erős sav konjugált bázisától várunk.
Példa \(\PageIndex{2}\)
Jósold meg, hogy az egyes reakciók egyensúlya balra vagy jobbra van-e az írottak szerint.
- \(NH^+_{4(aq)}+PO^{3-}_{4(aq)}+PO^{4(aq)} \rightleftharpoons NH_{3(aq)}+HPO^{2−}_{4(aq)}\)
- \(CH_3CH_2CO_2H_{(aq)}+CN^−_{(aq)} \rightleftharpoons CH_3CH_2CO^-_{2(aq)}+HCN_{(aq)}\)
Adott: egyensúlyi kémiai egyenlet
Kérdés: egyensúlyi helyzet
Stratégia:
Meghatározzuk a konjugált sav-bázis párokat minden reakcióban. Ezután a \(\PageIndex{1}\)és\(\PageIndex{2}\) táblázatok és az \(\PageIndex{2}\) ábra alapján határozza meg, hogy melyik az erősebb sav és bázis. Az egyensúly mindig a gyengébb sav-bázis pár kialakulásának kedvez.
Solution:
A konjugált sav-bázis párok \(NH_4^+/NH_3\) és \(HPO_4^{2-}/PO_4^{3-}\). A \(\PageIndex{1}\) és \(\PageIndex{2}\) táblázatok szerint az \(NH_4^+\) erősebb sav (\(pK_a = 9.25\)), mint a \(HPO_4^{2-}\) (pKa = 12,32), és a \(PO_4^{3-}\) erősebb bázis (\(pK_b = 1,68\)), mint a \(NH_3\) (\(pK_b = 4,75\)). Az egyensúly tehát jobbra esik, és a gyengébb sav-bázis pár kialakulásának kedvez:
\
A konjugált sav-bázis párok \(CH_3CH_2CO_2H/CH_3CH_2CO_2^-\) és \(HCN/CN^-\). A \(\PageIndex{1}\) táblázat szerint a HCN gyenge sav (pKa = 9,21) és a \(CN^-\) közepesen gyenge bázis (pKb = 4,79). A propionsav (\(CH_3CH_2CO_2H\)) azonban nem szerepel a \(\PageIndex{1}\) táblázatban. Ilyen helyzetben a legjobb, ha olyan hasonló vegyületet keresünk, amelynek sav-bázis tulajdonságai szerepelnek a listában. Például a propionsav és az ecetsav a karbonsav szénatomjához kapcsolódó csoportok kivételével azonosak (\(\(\ce{-CH_2CH_3}\) versus \(\(\ce{-CH_3}\))), így a két vegyület hasonló sav-bázis tulajdonságokkal rendelkezik. Különösen azt várnánk, hogy a propionsav \(pK_a\) értéke hasonló nagyságú legyen, mint az ecetsav \(pK_a\) értéke. (Valójában a propionsav \(pK_a\) értéke 4,87, míg az ecetsavé 4,76, ami a propionsavat valamivel gyengébb savvá teszi, mint az ecetsavat). A propionsavnak tehát lényegesen erősebb savnak kell lennie, mint a \(HCN\). Mivel az erősebb sav képezi a gyengébb konjugált bázist, azt jósoljuk, hogy a cianid erősebb bázis lesz, mint a propionát. Az egyensúly tehát jobbra fog feküdni, ami a gyengébb sav-bázis pár kialakulásának kedvez:
\
gyakorlat \(\PageIndex{1}\)
Jósold meg, hogy az egyes reakciók egyensúlya a leírtak szerint balra vagy jobbra esik.
- \(H_2O_{(l)}+HS^-_{(aq)} \rightleftharpoons OH^−_{(aq)}+H_2S_{(aq)}\)
- \(HCO^−_{2(aq)}+HSO^−_{4(aq)} \rightleftharpoons HCO_2H_{(aq)}+SO^{2-}_{4(aq)}\)
Válasz a
balra
Válasz b
balra
Összefoglaló
A sav-bázis reakciók mindig két konjugált sav-bázis párt tartalmaznak. Minden savhoz és minden bázishoz tartozik egy ionizációs állandó, amely megfelel a sav vagy bázis erősségének. Két olyan faj, amelyek csak egy protonban különböznek egymástól, konjugált sav-bázis párt alkotnak. Az ionizációs reakció egyensúlyi állandójának nagysága felhasználható a savak és bázisok relatív erősségének meghatározására. Egy gyenge sav vizes oldata esetén a disszociációs állandót savionizációs állandónak (\(K_a\)) nevezzük. Hasonlóképpen, egy gyenge bázis vízzel való reakciójának egyensúlyi állandója a bázisionizációs állandó (\(K_b\)). Bármely konjugált sav-bázis pár esetén \(K_aK_b = K_w\). Az \(pK_a\) kisebb értékei nagyobb savionizációs állandóknak és így erősebb savaknak felelnek meg. Ezzel szemben az \(pK_b\) kisebb értékei nagyobb bázisionizációs állandóknak és ezáltal erősebb bázisoknak felelnek meg. 25°C-on \(pK_a + pK_b = 14,00\). A sav-bázis reakciók mindig abba az irányba haladnak, amelyik a gyengébb sav-bázis párt eredményezi. Vizes oldatban nem létezhet \(H_3O^+\)-nál erősebb sav és \(OH^-\)-nél erősebb bázis, ami a kiegyenlítő hatásnak nevezett jelenséghez vezet. A poliprotikus savak (és bázisok) fokozatosan veszítenek (és nyernek) protonokat, a teljesen protonált faj a legerősebb sav, a teljesen deprotonált faj pedig a legerősebb bázis.
Kulcsegyenletek
- Sav ionizációs állandó: \=\dfrac{}{} \]
- Bázis ionizációs állandó: \= \dfrac{}{} \\]
- Egy konjugált sav-bázis pár \(K_a\) és \(K_b\) közötti összefüggés: \
- Az \(pK_a\) definíciója: \ \
- Az \(pK_b\) definíciója: \ \
- \(pK_b\): \ \
- Egy konjugált sav-bázis pár \(pK_a\) és \(pK_b\) közötti kapcsolat: \ \
Megosztók és hozzászólások
-
Stephen Lower, professor emeritus (Simon Fraser U.) Chem1 Virtual Textbook