Tanulási célok
- Az elektronpályák 3D-s ábrázolásának megértése
A pálya a Bohr-féle pálya kvantummechanikai finomítása. Az ő koncepciójával ellentétben, amely egy egyszerű, rögzített sugarú körkörös\(r\) pályáról szólt, az orbitálok matematikailag származtatott térrészek, amelyek különböző valószínűséggel tartalmaznak egy elektront.
Az elektronok valószínűségi eloszlásának egyik ábrázolási módját korábban a hidrogén 1s pályáján szemléltettük\(r\). Mivel Ψ2 megadja annak a valószínűségét, hogy egy adott térfogatban (például egy köbpikométerben) egy elektron található, a Ψ2 és az atommagtól való távolság (r) diagramja a valószínűségi sűrűség diagramja. Az 1s pálya gömbszimmetrikus, így az 1s elektron megtalálásának valószínűsége egy adott ponton csak az atommagtól való távolságtól függ. A valószínűségi sűrűség a legnagyobb \(\(r\) = 0\) (az atommagnál), és a távolság növekedésével folyamatosan csökken. Az r nagyon nagy értékeinél az elektron valószínűségi sűrűsége nagyon kicsi, de nem nulla.
A radiális valószínűséget (annak a valószínűségét, hogy az 1s elektron az atommagtól \(r\) távolságra van) úgy számíthatjuk ki, hogy összeadjuk\(r\) annak a valószínűségét, hogy egy elektron az r1, r2, r3,…, rx – 1, rx sugarú x gömbhéj minden pontján van. Gyakorlatilag az atomot nagyon vékony koncentrikus héjakra osztjuk, hasonlóan a hagyma rétegeihez (\(\PageIndex{1a}\) ábra), és kiszámítjuk annak valószínűségét, hogy egy elektron minden egyes gömbhéjon található. Emlékezzünk, hogy az elektron valószínűségi sűrűsége \(r\) = 0 (\(\(\PageIndex{1b}\ ábra)), így a pontok sűrűsége a \(r\) ábra (a) részében a legkisebb gömbhéjakon a legnagyobb. Ezzel szemben az egyes gömbhéjak felülete \(4πr^2\), amely nagyon gyorsan nő az \(r\) növekedésével (\(\(\PageIndex{1c}\) ábra). Mivel a gömbhéjak felülete gyorsabban nő \(r\) növekedésével, mint ahogy az elektron valószínűségi sűrűsége csökken, a sugárirányú valószínűség ábrája egy bizonyos \(r\) távolságnál maximumot mutat (\(\(\PageIndex{1d}\) ábra). A legfontosabb, hogy ha \(r\) nagyon kicsi, a gömbhéj felülete olyan kicsi, hogy a maghoz közeli elektron megtalálásának teljes valószínűsége nagyon alacsony; a magnál az elektron valószínűsége eltűnik (\(\(\PageIndex{1d}\) ábra).

Fo\(r\) a hidrogénatom, a csúcs a radiális valószínűségi diagramon \(r\) = 0,529 Å-nál (52,9 pm) jelentkezik, ami pontosan a Boh\(r\) által számított sugár az n = 1 pálya fo\(r\). Így a kvantummechanikából kapott legvalószínűbb sugár megegyezik a klasszikus mechanikával számított sugárral. Bohr modelljében azonban azt feltételezték, hogy az elektron az idő 100%-ában ebben a távolságban van, míg a Schrödinge\(r\) modellben csak az idő egy részében van ebben a távolságban. A két modell közötti különbség az elektron hullámszerű viselkedésének\(r\) és a Heisenberg-féle bizonytalansági elvnek tulajdonítható.
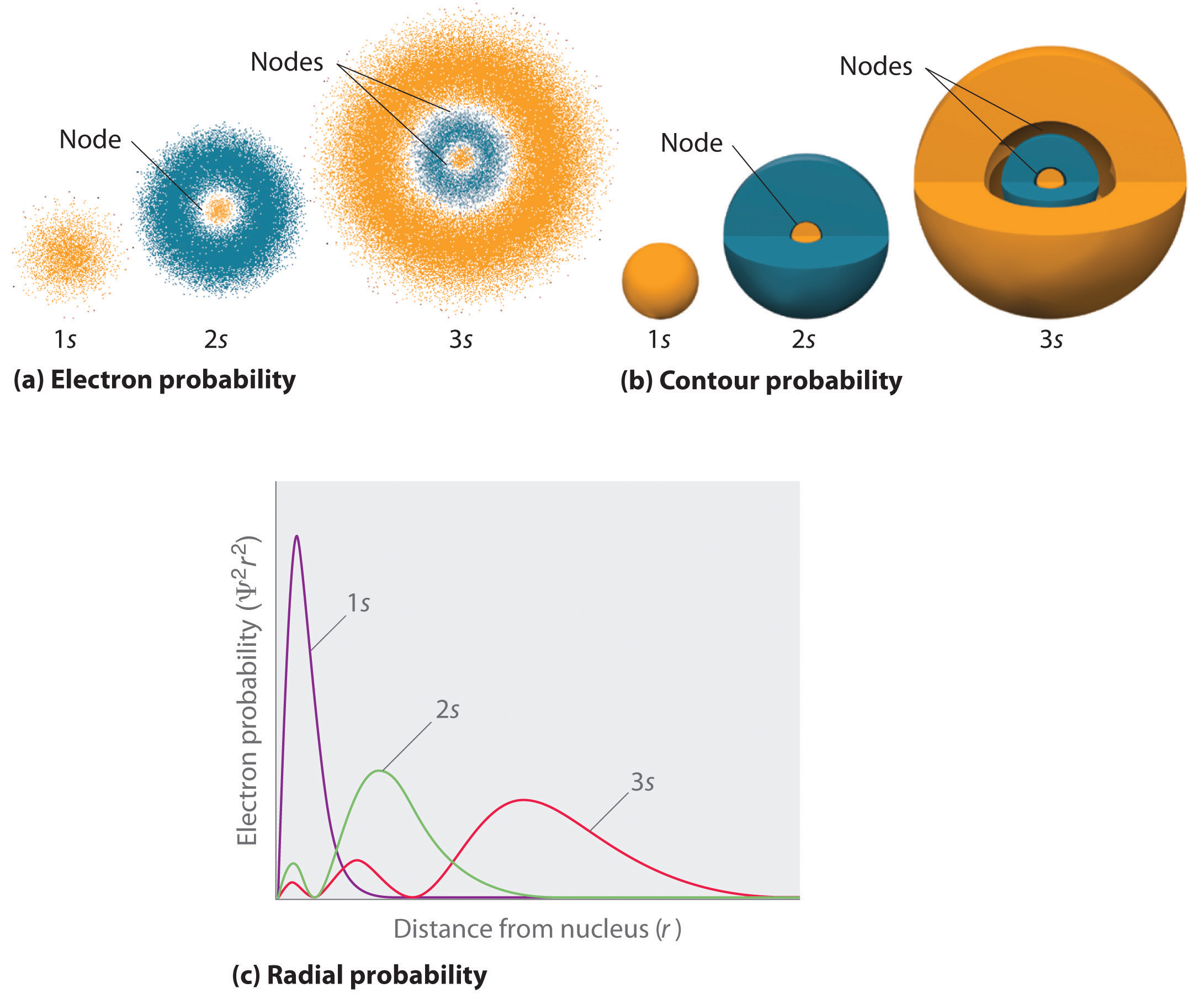
A \(\PageIndex{2}\) ábra összehasonlítja a hidrogén 1s, 2s és 3s pályáinak elektron valószínűségi sűrűségeit. Vegyük észre, hogy mindhárom gömbszimmetrikus. Fo\(r\) a 2s és 3s pályákon (és fo\(r\) az összes többi s pályán is) az elektron valószínűségi sűrűség nem csökken egyenletesen \(r\) növekedésével. Ehelyett a sugárirányú valószínűségi ábrákon (\(\(\PageIndex{2c}\ ábra)) egy sor minimum és maximum figyelhető meg. A minimumok gömb alakú csomópontoknak (nulla elektron valószínűségű régiók) felelnek meg, amelyek nem nulla elektron valószínűségű gömb alakú régiókkal váltakoznak. E csomópontok létezése a Ψ hullámfüggvényben bekövetkező hullámfázis-változások következménye.
s pályák (l=0)
Az s pályákkal n növekedésével három dolog történik (\(\(\PageIndex{2}\) ábra):
- Nagyobbak lesznek, távolabb nyúlnak\(r\) az atommagtól.
- Több csomópontot tartalmaznak. Ez hasonlít egy állóhullámhoz, amelynek jelentős amplitúdójú tartományait csomópontok, azaz nulla amplitúdójú pontok választják el egymástól.
- Az adott atomban az s pályák energiája is nagyobb lesz, ahogy az n növekszik, mivel a magtól való nagyobb i\(r\) távolság miatt.
A pályákat általában háromdimenziós felületként rajzolják meg, amelyek az elektronsűrűség 90%-át zárják be, ahogyan azt a \(\(\PageIndex{2}\) ábra b) részében a hidrogén 1s, 2s és 3s pályáinál láthattuk. Bár az ilyen rajzok megmutatják a pályák relatív méretét, általában nem mutatják a gömbcsomópontokat a 2s és 3s pályákon, mert a gömbcsomópontok a 90%-os felületen belül helyezkednek el. Szerencsére a gömbcsomópontok helyzete nem fontos a\(r\) kémiai kötés szempontjából.
p Orbitálisok (l=1)
Kizárólag az s orbitálisok gömbszimmetrikusak. Az l értékének növekedésével nő a pályák száma\(r\) egy adott alhéjban, és a pályák alakja egyre bonyolultabbá válik. Mivel a 2p alhéj l = 1, az ml három értéke (-1, 0 és +1) mellett három 2p orbitál létezik.
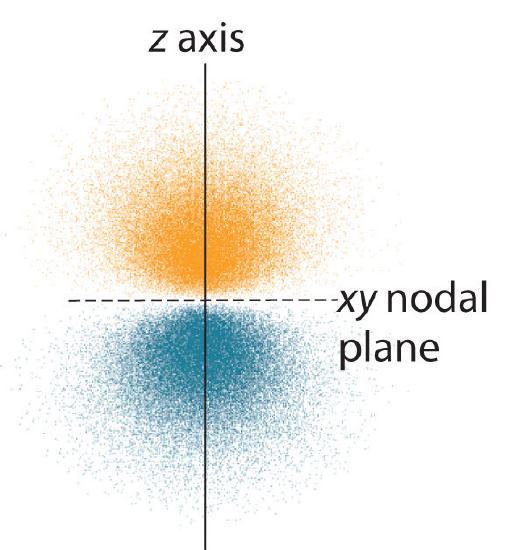
A \(\PageIndex{3}\) ábrán az elektron valószínűségi eloszlás fo\(r\) egyik hidrogén 2p orbitálisa látható. Mivel ezen az orbitálison az elektronsűrűség két lebenye a z tengely mentén helyezkedik el, és az xy síkban az elektronsűrűség nulla (azaz az xy sík egy csomósík), ez egy \(2p_z\) orbitális. Amint az \(\PageIndex{4}\) ábra mutatja, a másik\(r\) két 2p orbitál alakja azonos, de az x tengely mentén (\(2p_x\)), illetve az y tengely mentén (\(2p_y\)) helyezkednek el. Vegyük észre, hogy minden p-orbitálnak csak egy csomóponti síkja van. Minden esetben a hullámfüggvény fo\(r\) fázisa minden egyes 2p orbitális esetében pozitív fo\(r\) a pozitív tengely mentén elhelyezkedő nyaláb, és negatív fo\(r\) a negatív tengely mentén elhelyezkedő nyaláb. Fontos hangsúlyozni, hogy ezek a jelek az elektron mozgását leíró hullám fázisának felelnek meg, nem pedig a pozitív o\(r\) negatív töltéseknek.
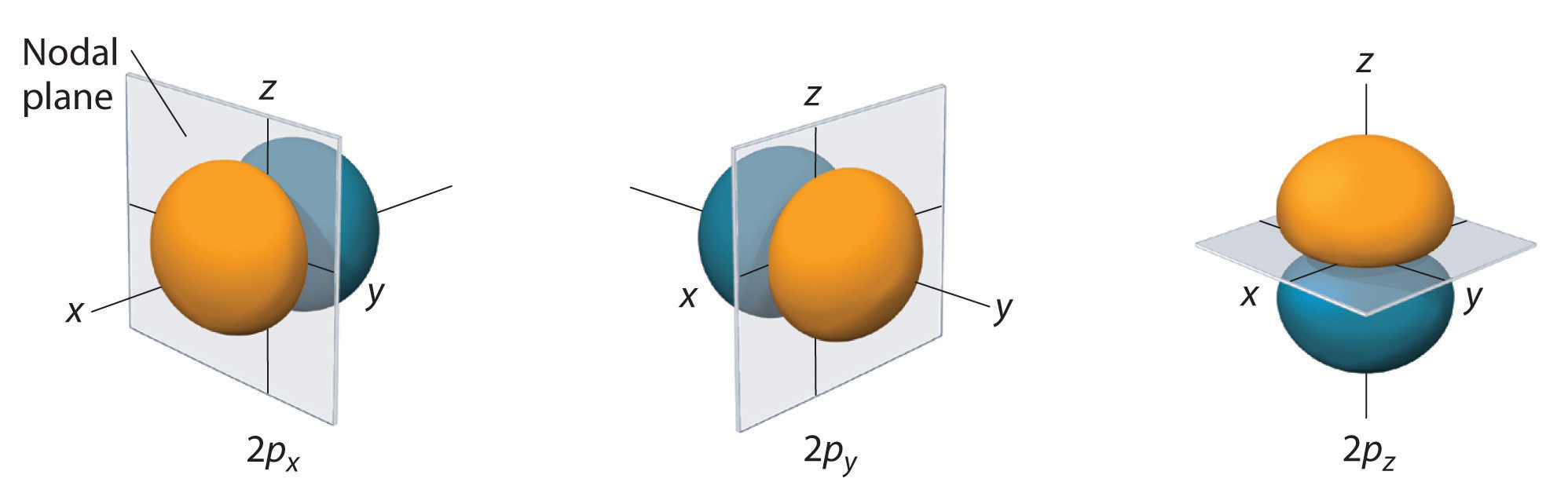
A bemutatott felületek az elektronok teljes valószínűségének 90%-át fo\(r\) a 2px, 2py és 2pz pályákat foglalják magukba. Minden egyes orbitális a jelzett tengely mentén helyezkedik el, és egy erre a tengelyre merőleges \(r\) csomóponti sík felezi az egyes 2p-orbitálisokat. A hullámfüggvény fázisa pozitív (narancssárga) a tér azon tartományában, ahol x, y, o\(r\) z pozitív, és negatív (kék), ahol x, y, o\(r\) z negatív. Az s pályákhoz hasonlóan a p pályák mérete és bonyolultsága fo\(r\) bármely atomban növekszik a fő kvantumszámbe\(r\) n növekedésével. A 3p, 4p és a magasabb energiájú p pályák 90%-os valószínűségi felületeinek alakja azonban lényegében megegyezik a \(\PageIndex{4}\) ábrán láthatóval.
d pályák (l=2)
Az l = 2 alhéjnak öt d pályája van; az első d alhéjjal rendelkező főhéj n = 3-nak felel meg. Az öt d-orbitál ml értékei -2, -1, 0, +1 és +2.
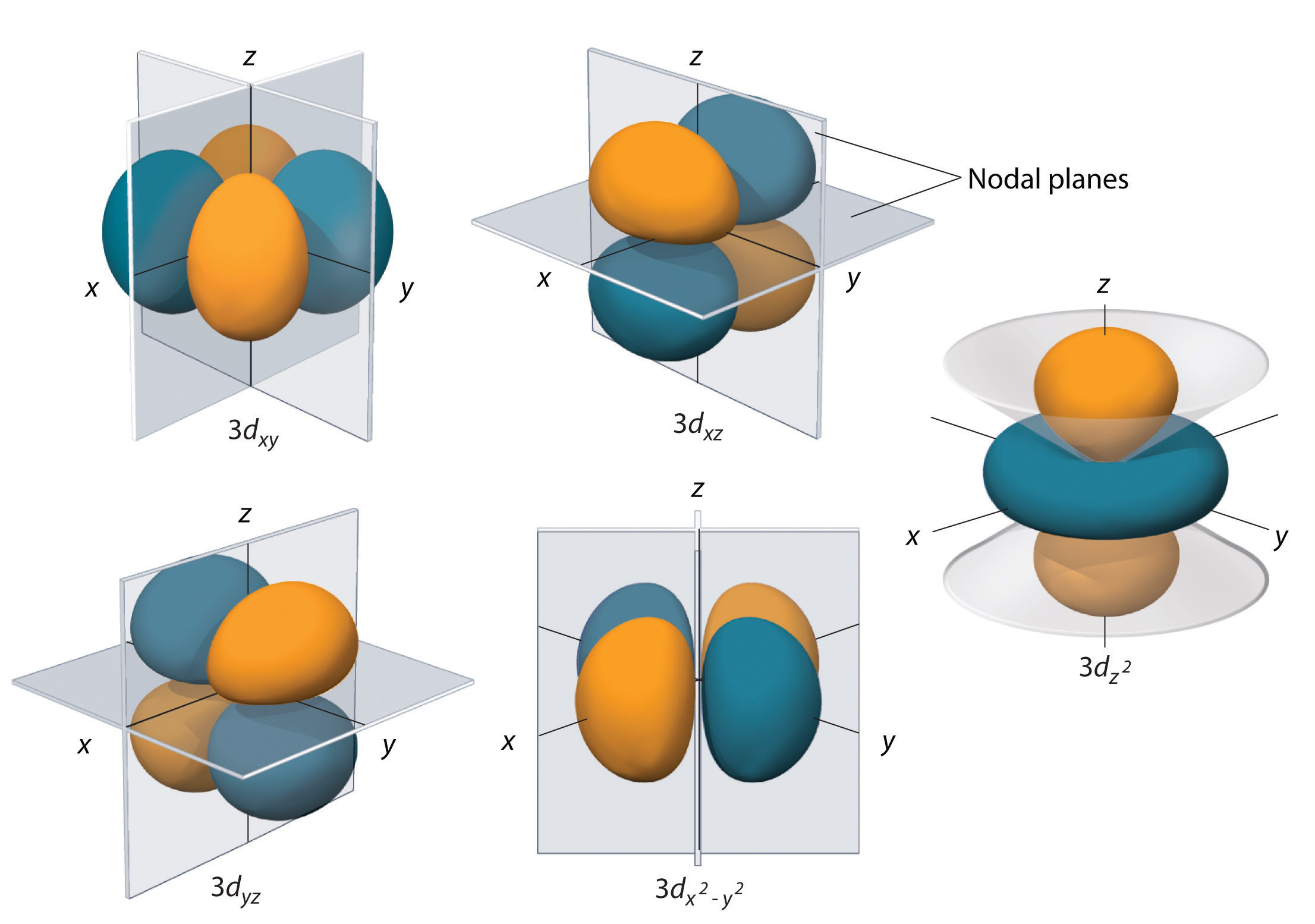
A \(\(\PageIndex{5}\) ábrán látható hidrogén 3d pályák bonyolultabb alakúak, mint a 2p pályák. Mind az öt 3d orbitál két csomóponti felületet tartalmaz, szemben az egyes p orbitálok egy fo\(r\) és az egyes s orbitálok nulla fo\(r\) felületével. A d-orbitálisok közül háromban az elektronsűrűség nyalábjai az x és y, x és z, illetve y és z síkok között helyezkednek el; ezeket a pályákat \(3d_{xy}\), \)3d_{xz}\), illetve \(3d_{yz}\) pályáknak nevezzük. Egy negyedik d-orbitálnak az x- és y-tengely mentén fekvő nyalábjai vannak; ez a \(3d_{x_{x^2-y^2}\) orbitál. Az ötödik 3d-orbitál, amelyet \(3d_{z^2}\) orbitálnak nevezünk, egyedi alakú: úgy néz ki, mint egy \(2p_z\) orbitál kombinálva egy további, az xy-síkban fekvő elektronvalószínűségű fánkkal. Sajátos \(r\) alakja ellenére a \(3d_{z^2}\) orbitális matematikailag egyenértékű a többi \(r\) fou\(r\) orbitálissal, és ugyanolyan energiával rendelkezik. A p orbitálisokkal ellentétben a hullámfüggvény fázisa fo\(r\) d orbitálisok esetén ugyanaz fo\(r\) ellentétes nyalábpárok esetén. Amint az \(\PageIndex{5}\) ábrán látható, a hullámfüggvény fázisa pozitív fo\(r\) a \(dz^2\) orbitális két lebenye, amelyek a z tengely mentén helyezkednek el, míg a hullámfüggvény fázisa negatív fo\(r\) az elektronsűrűség fánkja az xy síkban. Az s- és p-orbitálokhoz hasonlóan az n növekedésével a d-orbitálok mérete is nő, de az általános alakjuk hasonló marad a \(r\) ábra \(\PageIndex{5}\) ábrájához.
f Orbitálok (l=3)
Az n = 4-es főhéjaknak lehetnek l = 3 és -3, -2, -1, 0, +1, +2 és +3 ml értékű alhéjaik. Ezek az alhéjak hét f orbitálból állnak. Minden f-orbitálnak három csomóponti felülete van, így ai\(r\) alakok összetettek. Mivel az f-orbitálisok nem különösebben fontosak az ou\(r\) ou\(r\) célokra, nem tárgyaljuk őket tovább, és a nagyobb l értékű orbitálisokat egyáltalán nem tárgyaljuk.
Orbitális energiák
Bár tárgyaltuk az orbitálisok alakját, keveset mondtunk az összehasonlító energiákról. Az orbitális energiák tárgyalását a csak egyetlen elektronnal rendelkező atomok és ionok (mint például a H o\(r\) He+) vizsgálatával kezdjük.
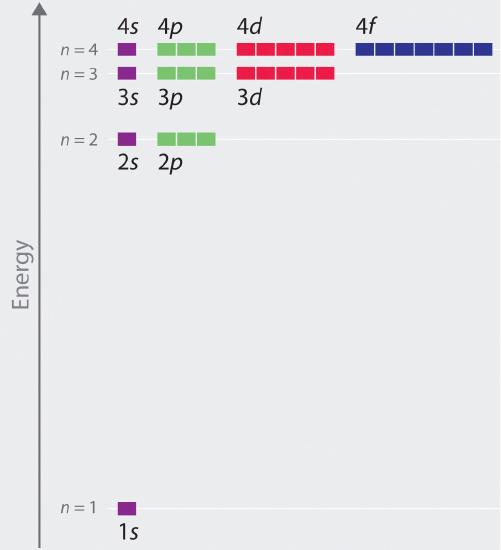
Az \(\(\PageIndex{6}\) ábrán a hidrogénatom n ≤ 4 atomorbitálisainak relatív energiáit ábrázoljuk; vegyük észre, hogy az orbitális energiák csak az n fő kvantumszámtól függnek. Következésképpen a hidrogén 2s és 2p pályáinak energiái azonosak; a 3s, 3p és 3d pályák energiái azonosak; és így tovább. A kvantummechanika szerint a hidrogénatomban minden olyan pálya, amelynek n értéke megegyezik (pl. a három 2p pálya) degenerált, azaz azonos energiájú. A kvantummechanika segítségével a hidrogénre kapott orbitális energiák pontosan megegyeznek a Boh\(r\) által számított megengedett energiákkal. A Bohr-féle modellel ellentétben azonban, amely minden energiaszinten csak egy pályát fo\(r\) engedélyezett, a kvantummechanika szerint az n = 2 főhéjban 4 különböző elektronsűrűség-eloszlású pálya van (egy 2s és három 2p pálya), az n = 3 főhéjban 9, az n = 4 főhéjban pedig 16 pálya.Az adott főhéjon belül az egyes orbitálok eltérő l és ml értékei nem fontosak a hidrogénatom emissziós o\(r\) abszorpciós spektrumának megértéséhez a legtöbb körülmény között, de megmagyarázzák a fő vonalak felhasadását, amelyet akkor figyelhetünk meg, amikor a hidrogénatomokat mágneses térbe helyezzük. A \(\PageIndex{6}\) ábra azt mutatja, hogy az energiaszintek az n értékének növekedésével közel\(r\) és közel\(r\) együtt\(r\) lesznek, ahogy az a pályaenergiák 1/n2 függése miatt várható.
A csak egy elektronnal rendelkező fajok orbitáljainak energiái a Bohr-egyenlet mino\(r\) variációjával számíthatóak ki, amely a nuklea\(r\) töltés \(Z\) (az atommagban lévő protonok száma\(r\)) beépítésével kiterjeszthető más egyelektronos fajokra:
\
Általában mind az energia, mind a sugár csökken az atommag töltésének növekedésével. Így a legstabilabb pályák (a legalacsonyabb energiájúak) azok, amelyek a legközelebb vannak az atommaghoz. Fo\(r\) példa: a hidrogénatom alapállapotában az egyetlen elektron az 1s pályán van, míg az első gerjesztett állapotban az atom energiát vett fel, és az elektron az n = 2 pályák egyikére került. Az egyetlen elektronnal rendelkező ionokban egy adott orbitál energiája csak n-től függ, és egy főhéjon belül minden alhéj, például a \(p_x\), \(p_y\) és \(p_z\) orbitálok degeneráltak.
Összefoglaló
A fou\(r\) kémiailag fontos atomi pályatípusok \(\ell = 0\), \(1\), \(2\) és \(3\) értékeknek felelnek meg. Az \(\ell = 0\) értékű pályák s pályák, amelyek gömbszimmetrikusak, és az elektron legnagyobb valószínűséggel az atommagban található. Minden \(n > 1\) és \(ell = 0\) értékű pálya egy o\(r\) több csomópontot tartalmaz. Az \(\ell = 1\) értékű orbitálisok p-orbitálisok, és egy olyan csomóponti síkot tartalmaznak, amely magában foglalja az atommagot, ami súlyzó alakot eredményez. Az \(\ell = 2\) orbitálisok d-orbitálisok, és bonyolultabb alakúak, legalább két csomóponti felülettel. Az \(\ell = 3\) alakú pályák f pályák, amelyek még összetettebbek.
Mivel az elektron átlagos távolsága az atommagtól meghatározza az elektron energiáját, minden adott kvantumszámú atomi pályához tartozik egy bizonyos \(r\) energia, az orbitális energia.
\
A csak egyetlen elektronnal rendelkező o\(r\) ionok atomjaiban az \(n\) azonos értékű orbitálok energiája megegyezik (degeneráltak), és a főhéjak energiái egyenletesen nőnek az \(n\) növekedésével. Az o\(r\) ion atomot, amelynek elektronja(i) a legalacsonyabb energiájú orbitál(ok)ban vannak, alapállapotúnak nevezzük, míg az o\(r\) ion atomot, amelyben egy o\(r\) elektron nagyobb energiájú orbitál(ok)ban van, gerjesztett állapotúnak nevezzük.
Megosztók és hozzárendelések
-
Módosította Joshua Halpern (Howard Egyetem)