Euler azonossága zavarba ejtőnek tűnik:

Ez egy általánosabb képletből ered:

Yowza — egy képzeletbeli exponens és a szinusz és koszinusz viszonyában vagyunk! És valahogy a pi-t bedugva -1-et kapunk? Lehet ez valaha is intuitív?

Az 1800-as évek matematikusa, Benjamin Peirce szerint nem:

Ez teljesen paradox; nem értjük, és nem tudjuk, mit jelent, de bebizonyítottuk, és ezért tudjuk, hogy ez az igazságnak kell lennie.

Argh, ettől a hozzáállástól felforr a vérem! A formulák nem bemagolandó varázsigék: meg kell, meg kell, meg kell találnunk a felismerést. Íme az enyém:

Euler képlete két egyenértékű módját írja le a körmozgásnak.

Ez minden? Ez a lenyűgöző egyenlet a körbeforgásról szól? Igen — és megérthetjük, ha néhány analógiára építünk:

• Az 1-es számból kiindulva tekintsük a szorzást olyan transzformációnak, amely megváltoztatja a számot: $1 \cdot e^{i \pi}$
• A szabályos exponenciális növekedés folyamatosan növeli az 1-et valamilyen ütemben egy bizonyos időtartam alatt; a képzeletbeli exponenciális növekedés folyamatosan forgatja az 1-et valamilyen időtartamra
• A “pi” időegységre való növekedés azt jelenti, hogy pi sugarú körben haladunk
• Ezért $e^{i \pi}$ azt jelenti, hogy 1-től indulunk és pi-t forgatunk (félkörben), hogy -1-re jussunk

Ez a magas szintű nézet, merüljünk el a részletekben. Egyébként, ha valaki azzal próbál lenyűgözni, hogy $e^{i \pi} = -1$, kérdezd meg az i-t az i-edik hatványig. Ha nem tudják végiggondolni, akkor az Euler-képlet még mindig egy varázsigét jelent számukra.

Frissítés: Írás közben arra gondoltam, hogy egy videó segíthet a gondolatok érthetőbb kifejtésében:

A cos(x) + i * sin(x)

Az egyenlőségjel túlterhelt. Néha úgy értjük, hogy “egy dolgot állítunk egy másikhoz” (például x = 3), máskor pedig úgy, hogy “ez a két dolog ugyanazt a fogalmat írja le” (például $\sqrt{-1} = i$).

Euler képlete az utóbbi: két olyan képletet ad, amely megmagyarázza, hogyan mozoghatunk egy körben. Ha a körmozgást trigonometriával vizsgáljuk, és x sugárban haladunk:

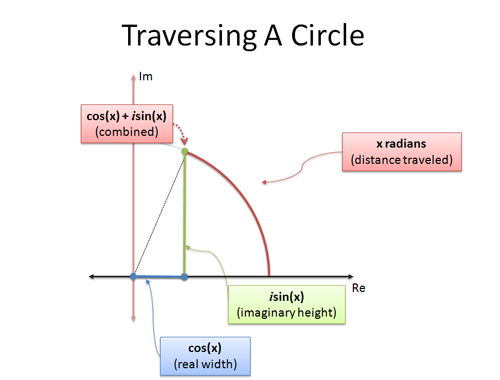
• cos(x) az x-koordináta (vízszintes távolság)
• sin(x) az y-koordináta (függőleges távolság)

A kijelentés

egy ügyes módja az x és y koordináták egyetlen számba sűrítésének. A “komplex számok kétdimenziósak” analógia segít abban, hogy egyetlen komplex számot úgy értelmezzünk, mint egy pozíciót egy körön.

Amikor x-et $\pi$-re állítjuk, akkor $\pi$ egységnyit haladunk az egységkör külső oldalán. Mivel a teljes kerület $2\pi$, a jó öreg $\pi$ félúton van, így a -1 ponton vagyunk.

Neato: Az Euler-képlet jobb oldala ($\cos(x) + i \sin(x)$) a körkörös mozgást írja le képzeletbeli számokkal. Most találjuk ki, hogyan valósítja meg ezt az egyenlet e oldala.

Mi az imaginárius növekedés?

Az x- és y- koordináták komplex számmá kombinálása trükkös, de kezelhető. De mit jelent a képzeletbeli exponens?

Lépjünk egy kicsit hátra. Amikor $3^4$-t látok, így gondolok rá:

• 3 a végeredménye annak, hogy azonnal (e segítségével) ln(3) sebességgel növekszik. Más szóval: $3 = e^{\ln(3)}$
• $3^4$ ugyanaz, mintha 3-ig növekednénk, de aztán 4x annyi ideig növekednénk. Tehát $3^4 = e^{\ln(3) \cdot 4} = 81$

Ahelyett, hogy a számokat önmagukban látnánk, úgy is gondolhatunk rájuk, mint valamire, amihez e-nek “hozzá kellett nőnie”. A valós számok, mint például a 3, ln(3) = 1,1 kamatlábat adnak, és ez az, amit e “összegyűjt”, miközben halad, folyamatosan növekszik.

A szabályos növekedés egyszerű: folyamatosan “tolja” a számot ugyanabba a valós irányba, amerre eddig ment. A 3 × 3 az eredeti irányba tolja, így háromszor nagyobb lesz (9).

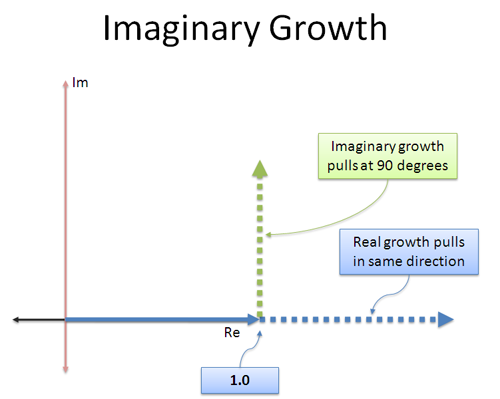
A képzeletbeli növekedés más: a “kamat”, amit keresünk, más irányba megy! Olyan ez, mint egy sugárhajtómű, amit oldalra csatoltak — ahelyett, hogy előre mennénk, 90 fokban kezdünk el tolni.

Az állandó ortogonális (merőleges) tolásban az a szép, hogy nem gyorsít vagy lassít — hanem forgat! Ha bármilyen számot veszünk és megszorozzuk i-vel, az nem változtatja meg a nagyságát, csak az irányt, amerre mutat.

Intuitívan így látom a folyamatos képzeletbeli növekedési ütemet: “Amikor növekedem, ne tolj előre vagy hátra abba az irányba, amerre már megyek. Forgass engem inkább.”

De nem kellene egyre gyorsabban és gyorsabban pörögnünk?

Én is elgondolkodtam ezen. A szabályos növekedés az eredeti irányunkban vegyül, tehát megyünk 1, 2, 4, 8, 16, minden alkalommal 2x szorozva és a valós számoknál maradva. Ezt tekinthetjük $e^{\ln(2)x}}$-nek, ami azt jelenti, hogy azonnal növekedjünk ln(2) sebességgel “x” másodpercig.

És hé — ha a növekedési sebességünk kétszer olyan gyors lenne, 2ln(2) vs ln(2), akkor ugyanúgy nézne ki, mintha kétszer olyan hosszú ideig növekednénk (2x vs x). Az e varázslata lehetővé teszi, hogy felcseréljük a sebességet és az időt; 2 másodperc ln(2) mellett ugyanolyan növekedés, mint 1 másodperc 2ln(2) mellett.

Most képzeljük el, hogy van valami tisztán képzeletbeli növekedési sebességünk (Ri), amely addig forgat minket, amíg el nem érjük az i-t, vagyis 90 fokkal felfelé. Mi történik, ha megduplázzuk ezt a sebességet 2Ri-re, kifordulunk a körből?

Nem! Ha 2Ri a sebességünk, az azt jelenti, hogy csak kétszer olyan gyorsan forogunk, vagy alternatívaként kétszer olyan sokáig forogunk R sebességgel, de a körön maradunk. Kétszer annyi ideig forogni azt jelenti, hogy most 180 fokot nézünk.

Mihelyt rájövünk, hogy valamilyen exponenciális növekedési sebességgel 1-től i-ig juthatunk, a sebesség növelése csak még jobban megpörget minket. Soha nem szabadulunk ki a körből.

Ha azonban a növekedési ütemünk komplex (a+bi vs Ri), akkor a valós rész (a) normális módon fog minket növelni, míg a képzeletbeli rész (bi) elforgat minket. De ne bonyolítsuk túl a dolgot: Euler képlete, $e^{ix}$, a tisztán képzeletbeli növekedésről szól, ami a körön tart minket (erről később).

Egy gyors józansági ellenőrzés

Az írás közben tisztáznom kellett magamban néhány kérdést:

Miért használjuk az $e^x$-t, nem az 1-es számot forgatjuk?

e azt a folyamatot reprezentálja, amikor 1-től indulunk, és 1 időegységig folyamatosan növekszünk 100%-os kamattal.

Amikor e-t írunk, akkor ezt az egész folyamatot egyetlen számban ragadjuk meg — e a folyamatos növekedés egész rigmusát reprezentálja. Tehát valójában $e^x$ azt mondja, hogy “1-től indul és x másodpercig folyamatosan 100%-kal növekszik”, és 1-től indul, ahogy akarjuk.

De mit csinál az i mint exponens?

Egy olyan szabályos exponens esetében, mint $3^4$, azt kérdezzük:

• Mi az implicit növekedési ráta? Növekszünk 1-től 3-ig (az exponens bázisáig).
• Hogyan változtathatjuk meg ezt a növekedési ütemet? Skálázzuk 4x-gyel (az exponens hatványával).

A növekedésünket “e” formátumba konvertálhatjuk: a pillanatnyi sebességünk ln(3), és növeljük ln(3) * 4-re. Megint csak az exponens hatványa (4) skálázta a növekedési sebességünket.

Ha a felső exponens i (mint $3^i$), akkor egyszerűen megszorozzuk az implicit növekedési sebességünket i-vel. Tehát ahelyett, hogy a sima régi ln(3)-mal növekednénk, ln(3)*i-vel növekedünk.

Az exponens felső része módosítja az alsó rész implicit növekedési ütemét.

A részletek

Nézzük meg közelebbről. Emlékezzünk e következő definíciójára:

Az $\frac{100\%}{n}$ azt a részkamatot jelenti, amelyet minden egyes mikroszkopikus időszakban megszereztünk. Feltételeztük, hogy a kamat mértéke 100% a valós dimenzióban — de mi lenne, ha 100% lenne a képzeletbeli irányban?

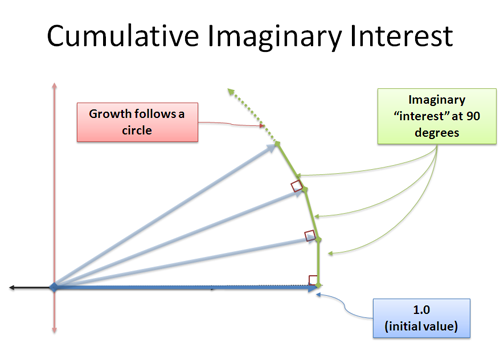
Most, az újonnan képzett kamatunk a 90 fokos irányban adódik hozzánk. Meglepő módon ez nem változtatja meg a hosszunkat — ez egy trükkös fogalom, mert látszólag olyan háromszöget alkot, ahol a hipotenúzának nagyobbnak kell lennie. Egy határértékkel van dolgunk, és a plusz távolság az általunk megadott hibahatáron belül van. Ezzel egy másik nap szeretnék foglalkozni, de higgye el, amit mondok: a folyamatos merőleges növekedés megforgatja. Ez a szinusz és a koszinusz szíve, ahol a változásunk merőleges az aktuális helyzetünkre, és egy körben mozgunk.

I egységnyi növekedést alkalmazunk végtelenül kis lépésekben, amelyek mindegyike 90 fokos szögben tol minket. Nincs “egyre gyorsabb és gyorsabb” forgás – ehelyett |i| = 1 (i nagysága) távolságot kúszunk a kerület mentén.

És hé — a kör körül kúszott távolság egy szög radiánban! Találtunk egy másik módot a körmozgás leírására!

A körmozgáshoz: Folyamatos változás 90 fokos szögben történő forgatással (más néven képzeletbeli növekedési sebesség).

Az Euler-képlet tehát azt mondja, hogy “exponenciális, képzeletbeli növekedés rajzol ki egy kört”. És ez a pálya ugyanaz, mintha a képzeletbeli síkban szinusz és koszinusz segítségével körbe mozognánk.

Az “exponenciális” szó ebben az esetben zavaró, mert állandó sebességgel haladunk a kör körül. A legtöbb vitában az exponenciális növekedésről azt feltételezik, hogy kumulatív, halmozódó hatású.

Egy pár példa

Nem hiszel nekem igazán, ugye? Íme néhány példa, és hogyan gondolkozzunk róluk intuitív módon.

Példa: $e^i$

Hol van az x? Á, csak 1. Intuitívan, anélkül, hogy elővennénk a számológépet, tudjuk, hogy ez azt jelenti, hogy “haladjunk 1 radiánt az egységkör mentén”. A fejemben azt látom, hogy “e” 100%-kal próbál 1-re nőni, mind egy irányba, de i folyamatosan mozgatja a golyót, és arra kényszeríti “1”-t, hogy a kör széle mentén nőjön:

Nem a legszebb szám, de ott van. Ne feledd, hogy a számológépedet radián üzemmódba állítsd, amikor ezt beütöd.

Példa: $3^i$

Ez trükkös — ez nem a szabványos formátumunkban van. De ne feledjük,

Az időszak végén 3x-os kezdeti növekedést akarunk, vagy ln(3) pillanatnyi sebességet. De jön az i, és megváltoztatja ezt a ln(3) sebességet “i * ln(3)”-ra:

Azt hittük, hogy egy szabályos ln(3) sebességgel fogunk átalakulni, egy kicsit gyorsabban, mint a 100%-os folyamatos növekedés, mivel e körülbelül 2,718. De ó nem, megpörgettem magunkat: most képzeletbeli sebességgel transzformálunk, ami azt jelenti, hogy csak forgunk körbe-körbe. Ha i egy szabályos szám lenne, mint például a 4, akkor 4x gyorsabban növekednénk. Most ln(3) sebességgel növekedünk, de oldalirányban.

Egy komplex számot kellene várnunk az egységkörön — a növekedési sebességben nincs semmi, ami növelné a méretünket. Az egyenlet megoldása:

Szóval, ahelyett, hogy “1” egységgel kerülnénk körbe (mint $e^i$), ln(3) egységgel kerülünk körbe.

Példa: $i^i$

Néhány hónappal ezelőtt ez még könnyekre fakasztott volna. Ma már nem! Bontsuk le az átalakításokat:

1-gyel kezdünk, és ezt akarjuk megváltoztatni. Mint a $3^i$ megoldása, mi az a pillanatnyi növekedési ütem, amit az i mint alap képvisel?

Hm. Normális esetben ln(x)-et csinálnánk, hogy megkapjuk azt a növekedési ütemet, ami ahhoz szükséges, hogy 1 időegység végén elérjük x-et. De egy képzeletbeli ráta esetén? Ezt át kell nudliznunk.

Hogy 1-től indulva i-ig növekedjünk, a kezdetektől fogva forgatni kell. Milyen gyorsan? Nos, 1 időegység alatt 90 fokot (pi/2 radián) kell elérnünk. Tehát a sebességünk $i \frac{\pi}{2}$. Ne feledjük, hogy a sebességünknek képzeletbelinek kell lennie, mivel forogunk, nem növekszünk! A sima régi $\frac{\pi}{2}$ körülbelül 1,57, és szabályos növekedést eredményez.

Ez érthető: ahhoz, hogy 1 egység végén 1,0-ból i legyen, ennyi idő alatt $\frac{\pi}{2}$ sugarat (90 fokot) kell forgatnunk. Tehát, hogy megkapjuk az “i”-t, használhatjuk a $e^{i \frac{\pi}{2}}$-t.

Fúú. Ez leírja az i-t mint alapot. Mi a helyzet az exponenssel?

Nos, a másik i azt mondja, hogy változtassuk meg az arányunkat — igen, azt az arányt, aminek a kiszámításával olyan sokáig foglalkoztunk! Tehát ahelyett, hogy $i \frac{\pi}{2}$ sebességgel forognánk, amit az i bázis jelent, átalakítjuk a sebességet:

Az i-k kioltják egymást, és a növekedési sebességet újra reálissá tesszük! Elforgattuk a rátánkat, és a negatív számok közé toltuk magunkat. A negatív növekedési ráta pedig azt jelenti, hogy zsugorodunk — számolnunk kell azzal, hogy $i^i$ kisebbé teszi a dolgokat. És ez így is van:

Tada! (Az “i^i” kifejezésre keress rá a Google-on, hogy használd a számológépét)

Vegyél egy kis lélegzetet: Intuitív módon rájöhetsz, hogyan kell viselkedniük a képzetes bázisoknak és a képzetes exponenseknek. Hűha.

És bónuszként kitaláltad az ln(i)-t — ahhoz, hogy $e^x$ i legyen, e-t forgassuk $\frac{\pi}{2}$ sugárral.

Példa: (i^i)^i

Kettős imaginárius exponens? Ha ragaszkodsz hozzá. Először is tudjuk, hogy a zárójelen belül mi lesz a növekedési ütemünk:

Megkapjuk a -pi/2 negatív (zsugorodó) növekedési ütemet. És most ezt a sebességet ismét i-vel módosítjuk:

És most már negatív forgásunk van! Egységnyi idő alatt $-\frac{\pi}{2}$ sebességgel megyünk körbe a kör körül. Mennyi ideig megyünk? Nos, ennek az exponensláncnak a legelején van egy implicit “1” időegység; az implicit alapértelmezés az, hogy 1 időegységig megyünk (ahogy $e = e^1$). 1 időegység $-\frac{\pi}{2}$ rádián (-90 fok) vagy -i!

És, csak a vicc kedvéért, ha ezt az őrült eredményt négyzetre állítjuk:

Ez “csak” kétszer annyi forgás: a 2 egy szabályos szám, így megduplázza a forgási sebességünket egy időegység alatt teljes -180 fokra. Vagy tekinthetjük úgy is, hogy kétszer egymás után -90 fokos elforgatást alkalmazunk.

Előre nagyon furcsa exponensek ezek. De az analógiáink segítségével nyugodtan el tudjuk fogadni őket.

Komplex növekedés

Egyszerre lehet valós és képzetes növekedésünk: a valós rész felfelé skáláz, a képzetes rész pedig elforgat minket:

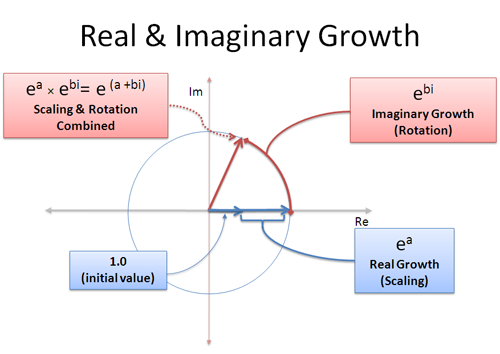
A komplex növekedési ütem, mint például (a + bi) a valós és képzetes növekedés keveréke. Az a valós rész, azt jelenti, hogy “növekedj 100%-kal a másodpercig”, a b képzeletbeli rész pedig azt, hogy “forogj b másodpercig”. Ne feledjük, a forgások nem élvezik az összetétel előnyeit, mivel folyamatosan más irányba “toljuk” — a forgás lineárisan adódik össze.

Ezt szem előtt tartva, bármilyen méretű kör bármely pontját ábrázolhatjuk (a+bi) segítségével! A sugár $e^a$, a szöget pedig $e^{bi}$ határozza meg. Ez olyan, mintha a számot két ciklusra tennénk be az expand-o-tronba: egyszer a megfelelő méretre növesztjük (a másodperc), másszor pedig a megfelelő szögre elforgatjuk (b másodperc). Vagy először elforgathatod, és csak utána növesztheted!

Tegyük fel, hogy tudni akarjuk a növekedés mértékét, hogy elérjük a 6 + 8i értéket. Ez valójában egy képzeletbeli szám természetes logaritmusát kérdezi: hogyan növeljük e-t, hogy megkapjuk (6 + 8i)?

• Sugár: Mekkora körre van szükségünk? Nos, a nagysága $\sqrt{6^2 + 8^2} = \sqrt{100} = 10$. Ami azt jelenti, hogy ln(10) = 2,3 másodpercig kell növekednünk, hogy elérjük ezt az összeget.
• Az elforgatandó összeg: Mekkora szöget zár be ez a pont? Az arctan segítségével kiszámolhatjuk: atan(8/6) = 53 fok = .93 radián.
• Az eredményt összeadva: ln(6+8i) = 2,3 + .93i

Ez azt jelenti, hogy a véletlenszerű (6 + 8i) pontot elérhetjük, ha $e^{2.3 + .93i}$.

Miért hasznos ez?

Euler képlete egy másik módszert ad a körmozgás leírására. De ezt már megtehettük a szinusz és a koszinusz segítségével is — mi olyan különleges?

Az egész a perspektíváról szól. A szinusz és a koszinusz a mozgást egy rácson írja le, vízszintes és függőleges koordinátákat rajzol ki.

Euler képlete polárkoordinátákat használ — mi a szög és a távolság? Ismét kétféleképpen írja le a mozgást:

• Rácsrendszer: Menj 3 egységet keletre és 4 egységet északra
• Poláris koordináták: Menj 5 egységet 53,13 fokos szögben

A feladattól függően a poláris vagy a derékszögű koordináták hasznosabbak. Az Euler-képlet segítségével átválthatunk a kettő között, hogy a feladathoz legmegfelelőbb eszközt használhassuk. Továbbá, mivel $e^{ix}$ átváltható szinuszra és koszinuszra, a trigonometriás képleteket átírhatjuk az e variációjaként, ami nagyon jól jön (nem kell megjegyezni a sin(a+b)-t, le lehet vezetni — erről majd máskor). És gyönyörű, hogy minden szám, legyen az valós vagy komplex, az e egy variációja.

De hasznosság, schmutility: a legfontosabb eredmény az a felismerés, hogy a zavarba ejtő egyenletek a megfelelő analógiákkal intuitívvá válhatnak. Ne hagyd, hogy az olyan gyönyörű egyenletek, mint az Euler-képlet, varázsigék maradjanak — építs az általad ismert analógiákra, hogy meglásd az egyenletben rejlő felismeréseket.

Boldog matematikát.

Függelék

A screencast szórakoztató volt, és a visszajelzéseket mindenképpen szívesen fogadjuk. Szerintem segít az ötletek felbukkanásában, és a cikk végigjárása segített megtalálni a hiányosságokat az intuíciómban.

• Brian Slesinsky-nek van egy szép előadása az Euler-képletről
• A vizuális komplex analízisnek van egy remek tárgyalása az Euler-képletről — lásd a 10. oldalt a Google Book Preview-ban
• Megtartottam egy előadást a Math and Analogies-on, amely az Euler-azonosságot vizuálisan jobban elmagyarázza:

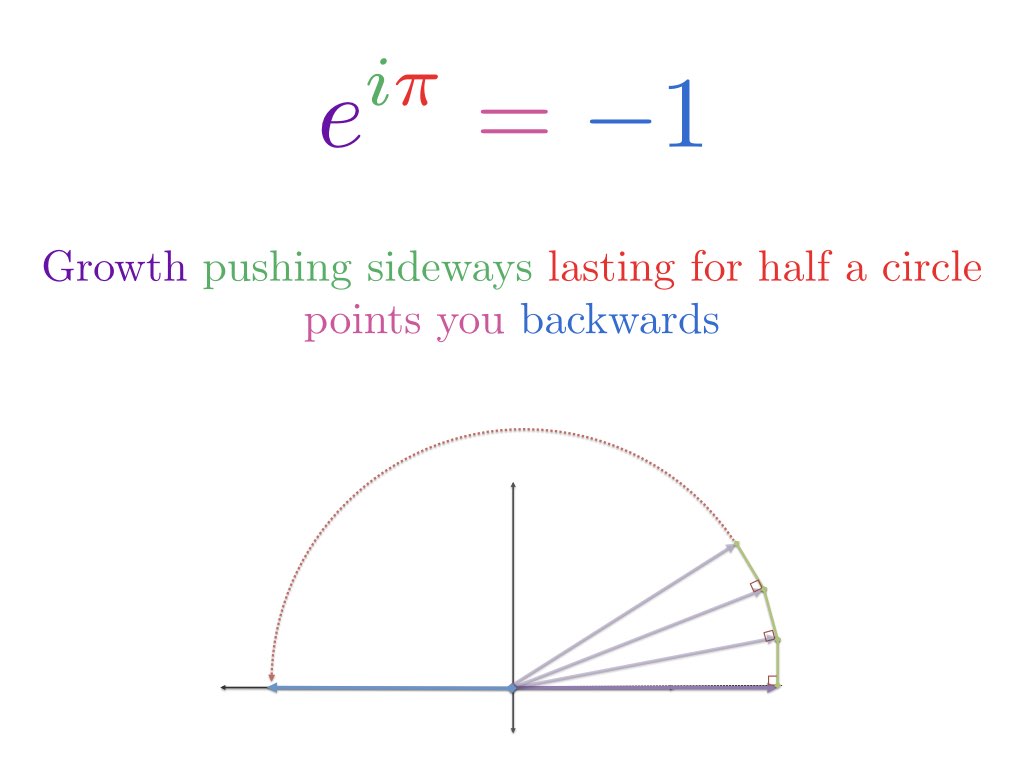
Más hozzászólások ebben a sorozatban

1. A Visual, Intuitive Guide to Imaginary Numbers
2. Intuitive Arithmetic With Complex Numbers
3. Understanding Why Complex Multiplication Works
4. Intuitive Guide to Angles, Degrees and Radians
5. Intuitive Understanding Of Euler’s Formula
6. An Interactive Guide To The Fourier Transform
7. Intuitive Guide to Convolution
8. A szinuszhullámok intuitív megértése
9. Intuitív útmutató a lineáris algebrához
10. A programozó intuíciója a mátrixszorzáshoz
11. Imagináris szorzás vs. Képzelt exponensek