Képzelj el egy papírnégyzetet, amely laposan fekszik az asztalodon. Megkérem, hogy csukja be a szemét. Hallod, ahogy a papír elmozdul. Amikor kinyitod a szemed, úgy tűnik, hogy a papír nem változott. Mit tehettem vele, amíg nem figyeltél?

Nyilvánvaló, hogy nem forgattam el a papírt 30 fokkal, mert akkor a papír másképp nézne ki.

Azt sem fordítottam meg, hogy átfordítottam egy vonalon, amely mondjuk az egyik sarkát egy másik él középpontjával köti össze. A papír másképp nézne ki, ha így tettem volna.

Azt azonban megtehettem volna, hogy elfordítom a papírt az óramutató járásával megegyező vagy ellentétes irányba 90 fok bármely többszörösével, vagy átfordítom az átlós vonalak vagy a vízszintes és függőleges vonalak valamelyikén.

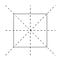
Az átalakulások szemléltetésének hasznos módja, ha megjelöljük a négyzet sarkait.

Az utolsó lehetőség, hogy nem csinálunk semmit. Ezt nevezzük identitás-átalakításnak. Ezeket együttesen a négyzet szimmetriatranszformációinak nevezzük.

A szimmetriatranszformációkat kombinálhatom, hogy más szimmetriatranszformációkat alkossak. Például a BD vonalszakasz két átfordítása az azonosságot eredményezi, akárcsak négy egymást követő 90 fokos, az óramutató járásával ellentétes irányú elforgatás. A függőleges vonal körüli megfordítás, amelyet a vízszintes vonal körüli megfordítás követ, a 180 fokos elforgatáshoz hasonlóan biztonságos hatást vált ki. Általában a szimmetriatranszformációk bármely kombinációja szimmetriatranszformációt eredményez. A következő táblázat a szimmetriatranszformációk összeállításának szabályait adja meg:

A táblázatban a 90, 180 és 270 indexű R az óramutató járásával ellentétes irányú 90, 180 és 270 fokos elforgatást jelöl, a H a vízszintes vonal körüli megfordítást, a V a függőleges vonal körüli megfordítást, az MD a bal felsőtől jobb alsóig tartó átló körüli megfordítást, az OD pedig a másik átló körüli megfordítást jelenti. A és B szorzatának megtalálásához menj az A sorára, majd a B oszlopára. Például: H∘MD=R₉₀.

A táblázatot nézve észrevehetünk néhány dolgot:

• A ∘ művelet asszociatív, ami azt jelenti, hogy A∘(B∘C) = (A∘B)∘C bármely A, B és C transzformációra.
• Minden A és B szimmetriatranszformációpárra az A∘B összetétel is szimmetriatranszformáció
• Van egy olyan e elem, hogy A∘e=e∘A minden A-ra
• Minden A szimmetriatranszformációra, van egy olyan egyedi szimmetriatranszformáció A-¹, hogy A∘A-¹=A-¹∘A=e

Ezért azt mondjuk, hogy egy négyzet szimmetriatranszformációinak gyűjteménye a kompozícióval együtt egy csoportnak nevezett matematikai struktúrát alkot. Ezt a csoportot D₄-nak, a négyzet diéderes csoportjának nevezzük. Ezek a struktúrák képezik e cikk tárgyát.

A csoport definíciója

A csoport ⟨G,*⟩ egy olyan G halmaz, amelynek van egy * szabálya a G bármely két elemének kombinálására, amely kielégíti a csoportaxiómákat:

Az absztraktban gyakran elhallgatjuk a *-ot, és a*b-t ab-nak írjuk, a *-ra pedig szorzásként hivatkozunk.

Nem szükséges, hogy a * kommutatív legyen, vagyis a*b=b*a. Ezt láthatjuk, ha megnézzük a D₄ táblázatot, ahol H∘MD=R₉₀, de MD∘H=R₂₇₀. Azokat a csoportokat, ahol a * kommutatív, Neils Abel után abeli csoportoknak nevezzük.

Az abeli csoportok inkább a kivételek, mint a szabály. Egy másik példa a nem abeliánus csoportra a kocka szimmetriatranszformációi. Vegyük csak a tengelyek körüli forgatásokat:

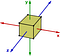
Ha először 90 fokot forgatok az óramutató járásával ellentétes irányban az y tengely körül, majd 90 fokot az óramutató járásával ellentétes irányban a z tengely körül, akkor más lesz az eredménye, mintha 90 fokot forgatnék a z tengely körül, majd 90 fokot az y tengely körül.

Egy elem lehet a saját inverze. Tekintsük azt a csoportot, amely 0-ból és 1-ből áll a bináris összeadás műveletével. Táblázata:

Az 1 nyilvánvalóan a saját inverze. Ez is egy abéliumos csoport. Ne aggódj, a legtöbb csoport nem ilyen unalmas.

Még néhány példa csoportokra:

• Az egész számok halmaza összeadással.
• A 0-t nem tartalmazó racionális számok halmaza szorzással.
• A xⁿ-1=0 polinomegyenlet megoldásainak halmaza, az úgynevezett n-edik egységgyök szorzással.

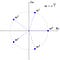
Az egység 5. gyökének megoldását jelentő x⁵-1=0

Itt van néhány példa, amelyek nem csoportok:

• A természetes számok halmaza összeadás alatt nem csoport, mert nincsenek inverzei, amelyek a negatív számok lennének.
• A 0-t is tartalmazó racionális számok halmaza szorzással nem csoport, mert nincs olyan q racionális szám, amelyre 0/q=1, tehát nem minden elemnek van inverze.

Group structure

A csoport sokkal több, mint egy paca, amely kielégíti a négy axiómát. Egy csoportnak lehet belső szerkezete, és ez a szerkezet nagyon bonyolult lehet. Az absztrakt algebra egyik alapvető problémája annak meghatározása, hogy hogyan néz ki egy csoport belső szerkezete, mivel a valóságban a ténylegesen vizsgált csoportok sokkal nagyobbak és bonyolultabbak, mint az itt megadott egyszerű példák.

A belső szerkezet egyik alapvető típusa az alcsoport. Egy G csoportnak akkor van H alcsoportja, ha H G részhalmaza és:

• Az a,b∈H, a*b∈H és b*a∈H
• A∈H, a-¹∈H
• Az azonosság H egyik eleme

H≠G esetén H-t saját alcsoportnak mondjuk. G azon alcsoportját, amely csak az azonosságból áll, triviális alcsoportnak nevezzük.

Egy nem-abeli csoportnak lehetnek kommutatív alcsoportjai. Tekintsük a bevezetőben tárgyalt négyzetes déderes csoportot. Ez a csoport nem abéliumos, de a forgások alcsoportja abéliumos és ciklikus:

Most két csoportszerkezeti példát adunk.

Még ha egy G csoport nem abéliumos, akkor is előfordulhat, hogy van G elemeinek egy olyan gyűjteménye, amely mindennel ingadozik G-ben. Ezt a gyűjteményt G középpontjának nevezzük. A C központ G egy alcsoportja. Bizonyítás:

Tegyük fel, hogy f egy olyan függvény, amelynek mind a tartománya, mind a tartománya G. Az f periódusa egy olyan a∈G elem, hogy f(x)=f(ax) minden x∈G-re. Az f periódusainak P halmaza G egy alcsoportja. Bizonyítás:

A véges csoportok végesen generáltak

Láttuk, hogy a ciklikus csoportokat egyetlen elem generálja. Ha egy G csoport minden elemét felírhatjuk G egy (nem feltétlenül saját) A részhalmazának termékeként, akkor azt mondjuk, hogy A generálja G-t, és ezt úgy írjuk, hogy G=⟨A⟩. A leginkább “na, duh” bizonyítás, amit valaha is láttál, az a bizonyítás, hogy minden véges csoportot véges generáló halmaz generál:

• Legyen G véges. G minden eleme G két másik elemének a szorzata, tehát G=⟨G⟩. QED.

A cikket egy alkalmazással zárjuk.

Hibamentes kommunikáció

A digitális információ továbbításának legegyszerűbb módja, ha fix hosszúságú bináris karakterláncokba kódoljuk. Egyetlen kommunikációs séma sem teljesen interferenciamentes, így mindig fennáll annak a lehetősége, hogy rossz adat érkezik. A maximális valószínűségű dekódolás módszere egyszerű és hatékony módszer az átviteli hibák felismerésére és kijavítására.

Legyen 𝔹ⁿ az n hosszúságú bináris karakterláncok vagy szavak halmaza. Egyszerűen megmutatható, hogy 𝔹ⁿ egy abéli csoport a hordozás nélküli bináris összeadás alatt (tehát például 010+011=001). Vegyük észre, hogy minden elem a saját inverze. A C kód 𝔹ⁿ egy részhalmaza. A következő példa egy 𝔹⁶-kódra:

C = {000000, 001011, 010110, 011101, 100101, 101110, 110011, 111000}

A kód elemeit kódszavaknak nevezzük. Csak a kódszavak kerülnek továbbításra. Hibáról akkor beszélünk, ha az interferencia megváltoztatja az átvitt szó egy bitjét. Két a és b kódszó közötti d(a,b) távolság azon számjegyek száma, amelyekben a két kódszó különbözik. Egy kód minimális távolsága a legkisebb távolság bármely két kódszó között. Az iménti példakód esetében a minimális távolság három.

A maximális valószínűségű dekódolás módszerében, ha kapunk egy x szót, amely hibát tartalmazhat, a vevőnek az x-et olyan a kódszóként kell értelmeznie, hogy d(a,x) minimális legyen. Megmutatom, hogy egy m minimális távolságú kód esetén ez mindig képes (1) az m bitnél kevesebbet változtató hibákat felismerni, és (2) az ½(m-1) vagy annál kevesebb bitet változtató hibákat kijavítani.

Példakódunkban m=3 és a 011101 kódszó körüli ½(m-1)=1 sugarú gömb {011101, 111101, 001101, 011001, 010101, 011111, 011100}. Ha tehát a vevő ezen szavak bármelyikét fogadja, akkor tudja, hogy a 011101-et kellett volna fogadnia.

Ez mind szép és jó, de mi köze van mindennek a csoportelmélethez? A válasz abban rejlik, hogy valójában hogyan állítjuk elő azokat a kódokat, amelyekkel ez a módszer dolgozik.

Egy 𝔹ⁿ kód lehetséges, hogy alcsoportot képezzen. Ebben az esetben azt mondjuk, hogy a kód egy csoportkód. A csoportkódok véges csoportok, tehát végesen generáltak. Megnézzük, hogyan állíthatunk elő egy kódot egy generáló halmaz megtalálásával.

Egy kódot úgy lehet megadni, hogy minden kódszó első néhány bitjét információs biteknek, a végén lévő biteket pedig paritásbiteknek nevezzük. Példánk C kódjában az első három bit az információs bitek, az utolsó három pedig a paritásbitek. A paritásbitek kielégítik a paritás-ellenőrzési egyenleteket. A A₁A₂A₃A₄A₅A₆ kódszó esetében a paritásegyenletek A₄=A₁+A₂, A₅=A₂+A₃ és A₆=A₁+A₃. A paritásegyenletek a hibák elleni védelem egy újabb rétegét biztosítják: ha bármelyik paritásegyenlet nem teljesül, akkor hiba történt.

A következőt tesszük. Tegyük fel, hogy m információs bitet és n paritásbitet tartalmazó kódszavakat akarunk. A csoportkód előállításához írjunk egy m soros és m+n oszlopos mátrixot. Az első m oszlopok által alkotott blokkba írjuk be az m×m azonossági mátrixot. A j oszlopba m+1≤j≤m_n esetén írjunk 1-et a k-adik sorba, ha Aₖ szerepel az Aⱼ paritásbit paritásegyenletében, és 0-t egyébként. Példakódunkban a mátrix:

Egy ilyen mátrixot a csoportkód generáló mátrixának nevezzük. Közvetlenül ellenőrizhetjük, hogy a sorok generálják C-t:

Minden generáló mátrix sorai generáló halmazt alkotnak egy C csoportkódhoz. Bizonyítás:

• Identitás és inverzek: Bármelyik sor önmagához adva adja az identitást, egy minden nullából álló karakterláncot.
• Zárás: Ha A,B∈C, akkor A és B a generáló mátrix sorainak összege, tehát A+B szintén a generáló mátrix sorainak összege. Tehát A+B∈C.

Ezzel tudunk kódot generálni, most megmutatom, hogyan generálhatunk egy hasznos kódot.

Meghatározzuk, hogy a w(x) súly az x-ben lévő egyesek számát jelenti. Például w(100101)=3. Nyilvánvaló, hogy w(x)=d(x,0), ahol a 0 egy olyan szó, amelynek minden számjegye nulla. Egy kód minimális súlya W annak a nem nulla kódszónak a súlya, amelynek a kódban a legkevesebb egyes van. Egy m minimális távolságú kód esetén d(x,0)≥m, tehát w(x)≥m, tehát W=m.

Memlékezzünk arra, hogy ahhoz, hogy egy szót kódszónak tekintsünk, ki kell elégítenie egy sor paritásellenőrzési egyenletet. Példánk kódja esetében ezek a következők: A₄=A₁+A₂, A₅=A₂+A₃, és A₆=A₁+A₃. Ezeket lineáris rendszerként is felírhatjuk:

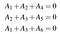
Ami maga is felírható a pontproduktumokkal:

Vagy kompaktabb formában Ha=0, ahol a=(A₁,A₂,A₃,A₄,A₅,A₆) és H a kód paritásellenőrző mátrixa:

Közvetlen számítással ellenőrizhetjük, hogy ha w(a)≤2, akkor nem lehet Ha=0. Általában a minimális súly t+1, ahol t a legkisebb olyan szám, hogy H t oszlopainak bármelyik gyűjteménye nem nulla összegű (azaz lineárisan független). Ennek bizonyítása egy kicsit túl messzire vezetne minket a lineáris algebrába.

Ha ez megijeszt, ne aggódj. Enélkül is előállíthatunk néhány nagyon jó kódot, ha kihasználjuk azt a tényt, hogy az imént említett eredmény azt jelenti, hogy ha H minden oszlopa nem nulla és nincs két egyenlő oszlop, akkor a minimális súly, és így a kód minimális távolsága legalább három. Ez nagyon jó: ha a kommunikációs rendszerünkben várhatóan minden száz átvitt szóra jut egy bit hiba, akkor csak minden tízezer átvitt szóból egy lesz korrigálatlan hibás, és minden egymillió átvitt szóból egy lesz fel nem fedezett hibás.

Így most már van egy receptünk arra, hogy m információs bitet és n paritásbitet tartalmazó kódszavakra használható kódot állítsunk elő a maximális valószínűségű detektálási séma számára:

• Készítsünk egy m+n oszlopos és n soros mátrixot. Töltsük ki a mátrixot egyesekkel és nullákkal úgy, hogy két oszlop ne legyen azonos, és egyetlen oszlop se legyen csak nulla.
• A kapott paritásellenőrző mátrix minden sora megfelel az egyik paritásbit-egyenletnek. Írja fel őket egyenletrendszerként, és oldja meg úgy, hogy minden paritásbitet az információs bitekkel írjon fel.
• Készítsen egy m+n oszlopos és m soros mátrixot. Az első m oszlopok által alkotott blokkba írjuk be az m×m azonossági mátrixot. A j oszlopba m+1≤j≤m_n esetén a k-adik sorba írjunk 1-et, ha Aₖ szerepel az Aⱼ paritásbit paritási egyenletében, és 0-t egyébként.
• A mátrix sorai egy legalább hármas minimális távolságú kódcsoport generátorai. Ezt a kódot fogjuk használni.

Tegyük fel például, hogy egy egyszerű, nyolc szóból álló kódra van szükségem, és csak alapvető hibadetektálásra van szükségem, korrekcióra nem, így megúszom a minimális távolságot kettővel. Három információs bitet és két paritásbitet akarok. Leírom a következő paritásellenőrző mátrixot:

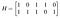
Az oszlopok két párja egyenlő, tehát a legkisebb t, amelyre a t oszlopok bármely gyűjteménye lineárisan független, egy, tehát a minimális súly, és így a minimális távolságom is kettő lesz. A sorok az A₄=A₁+A₃ és A₅=A₁+A₂+A₃ paritásellenőrző egyenleteket ábrázolják. Az én generáló mátrixom tehát:

És ennek a mátrixnak a sorai generálják a kódcsoportot:

• {00000, 00111, 01001, 01110, 10011, 10100, 111010, 11101}

Záró megjegyzések

Az absztrakt algebra mély és messzemenő következményekkel járó téma, de nagyon könnyen tanulható is. A lineáris algebra néhány futó említésétől eltekintve szinte minden, amit itt tárgyaltam, elérhető olyasvalaki számára is, akinek csak középiskolai algebrája volt.

Amikor először jött az ötlet, hogy megírjam ezt a cikket, nagyon szerettem volna a Rubik-kockáról beszélni, de végül egy olyan példát akartam választani, amelyet csak a csoportelmélet legalapvetőbb ötleteivel lehet kezelni. Ráadásul a Rubik-kocka csoportjáról annyi mondanivaló van, hogy megérdemel egy önálló cikket, úgyhogy az hamarosan jön.

A főiskolai absztrakt algebrai kurzusaim Charles Pinter A Book of Abstract Algebra című könyvén alapultak, ami egy közérthető feldolgozás. Az ebben a cikkben szereplő példákat némi módosítással mind Pintertől kölcsönöztem.

Végszóként megjegyzem, hogy a nem idézett képek az én eredeti munkáim, és felhasználhatóak, ha hivatkozunk rájuk. Mint mindig, most is örömmel fogadok minden javítást vagy felvilágosításra vonatkozó kérést.