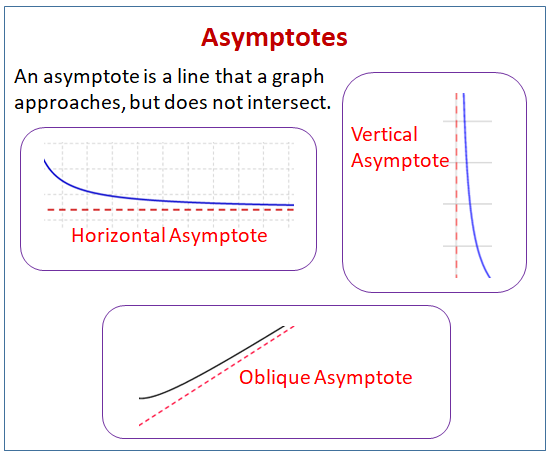
Aszimptota egy olyan vonal, amelyet egy grafikon megközelít, de nem metszi.
Ebben a leckében megtanuljuk, hogyan találjuk meg a racionális függvények függőleges aszimptotáit, vízszintes aszimptotáit és ferde (ferde) aszimptotáit.
Kapcsolódó témák:
Még több lecke a számtanról

A következő ábrán az aszimptoták különböző típusai láthatóak: vízszintes aszimptoták, függőleges aszimptoták és ferde aszimptoták. További példákért és megoldásokért görgess lefelé az oldalon az aszimptoták megtalálására.

Hogyan határozzuk meg a függőleges aszimptotát?

1. módszer: Használjuk a függőleges aszimptota definícióját

Az x = a egyenest az y = f(x) görbe függőleges aszimptotájának nevezzük, ha az alábbi állítások közül legalább egy igaz.

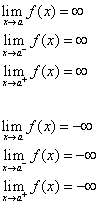
2. módszer:

Racionális függvények esetén a függőleges aszimptoták olyan függőleges egyenesek, amelyek a nevező nulláinak felelnek meg.
Adott a racionális függvény, f(x)

1. lépés: írjuk fel f(x)-t redukált formában

2. lépés: ha x – c egy tényező a nevezőben, akkor x = c a függőleges aszimptotája.

Példa:

Keresd meg a

függőleges aszimptotáit

Megoldás:

1. módszer: Használjuk a függőleges aszimptota definícióját.

Ha x közel van 3-hoz, de nagyobb, mint 3, akkor az x – 3 nevezője kis pozitív szám, és 2x közel van 8-hoz. Tehát egy nagy pozitív szám.

Intuitív módon látjuk, hogy

Hasonlóképpen, ha x közel van 3-hoz, de kisebb, mint 3, akkor x – 3 egy kis negatív szám és 2x közel van 8-hoz. Tehát egy nagy negatív szám.

Az x = 3 egyenes a függőleges aszimptota.

2. módszer:

1. lépés: f(x) már redukált formában van.

2. lépés: A nevező x – 3, tehát a függőleges aszimptota x = 3-nál van.

Racionális függvények függőleges aszimptotáinak megtalálása

Mit kell keresnünk, hogy megtaláljuk a racionális függvények függőleges aszimptotáit.

• Lépésről-lépésre megoldások megjelenítése

Racionális függvények függőleges aszimptotái: Quick Way to Find Them

Példa racionális függvények függőleges aszimptotáinak megtalálására.

• Lépésről-lépésre megoldások megjelenítése

How to find vertical asymptotes for rational functions

• Show Step-by-step Solutions

How to determine the horizontal Asymptote?

1. módszer: Használjuk a vízszintes aszimptota definícióját

Az y = L egyenest az y = f(x) görbe vízszintes aszimptotájának nevezzük, ha vagy

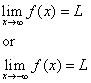
2. módszer:

Az f(x) racionális függvényre

Ha a számlálóban az x foka kisebb, mint a nevezőben az x foka, akkor y = 0 a vízszintes aszimptota.

Ha x foka a számlálóban egyenlő x fokával a nevezőben, akkor y = c, ahol c-t a vezető együtthatók osztásával kapjuk.

Példa:

Keresd meg a függvény vízszintes és függőleges aszimptotáit.

Megoldás:

1. módszer:

A számlálót és a nevezőt is osszuk el x-szel.

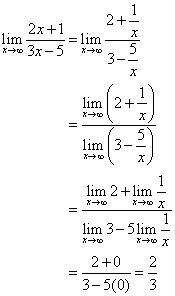
A vonal a vízszintes aszimptota.

2. módszer:

A számlálóban lévő x foka egyenlő a nevezőben lévő x fokával.

A vezető együtthatókat osztva

A vonal a vízszintes aszimptota.

Rövidítés a racionális függvények vízszintes aszimptotáinak megtalálásához

Egy pár trükk, amivel a racionális függvények vízszintes aszimptotáinak megtalálása nagyon egyszerű

• Lépésről lépésre megoldások megjelenítése

Ez a videó a vízszintes aszimptoták alapvető áttekintését adja. Meghatározzuk, hogy az adott racionális függvényeknek vannak-e vízszintes aszimptotái, és mik azok.

• Lépésről-lépésre megoldások megjelenítése

Ebben a videóban részletesebben foglalkozunk a vízszintes aszimptoták szabályaival.

• Lépésről-lépésre megoldások megjelenítése

Dőlő aszimptota vagy ferde aszimptota

Egyes görbéknek ferde aszimptotái vannak, vagyis sem vízszintesek, sem függőlegesek.

Ha akkor az y = mx + b egyenest ferde vagy ferde aszimptotának nevezzük, mert az y = f(x) görbe és az y = mx + b egyenes függőleges távolsága közelít a 0-hoz.

Racionális függvények esetében ferde aszimptoták akkor fordulnak elő, ha a számláló fokozata eggyel több, mint a nevező fokozata. Ilyen esetben a ferde aszimptota egyenletét hosszú osztással lehet megtalálni.

Példa:

Keresd meg a

függvény aszimptotáit:

Mivel az x2 + 1 nevezője sosem 0, nincs függőleges aszimptota.

Mivel az x foka a számlálóban nagyobb, mint az x foka a nevezőben, nincs vízszintes aszimptota.

Mivel az x foka a számlálóban eggyel nagyobb, mint az x foka a nevezőben, hosszú osztással megkaphatjuk a ferde aszimptotát.

Tehát az y = x egyenes a ferde aszimptota.

Racionális függvények ferde aszimptotáinak megtalálása

Ez a videó leírja, mikor van egy racionális függvénynek ferde aszimptotája, röviden ismerteti, mi az a ferde aszimptota, majd két példát mutat be.

• Lépésről-lépésre megoldások megjelenítése

Racionális függvény aszimptotáinak megtalálása (függőleges, vízszintes és ferde/ ferde aszimptoták)

Ez a videó bemutatja, hogyan kell megtalálni egy racionális függvény függőleges aszimptotáit és ferde/ ferde aszimptotáit.

• Lépésről-lépésre megoldások megjelenítése

Egy racionális függvény összes aszimptotájának megtalálása (függőleges, vízszintes, ferde / ferde)

Itt megnézünk egy függvényt és megtaláljuk a függőleges aszimptotát, valamint megállapítjuk, hogy vízszintes aszimptoták nincsenek, de ferde aszimptota igenis létezik. Ezután hosszú osztással megtaláljuk a ferde aszimptotát.

• Lépésről-lépésre megoldások megjelenítése

Kipróbáld az alábbi ingyenes Mathway kalkulátort és feladatmegoldót a különböző matematikai témák gyakorlásához. Próbáld ki a megadott példákat, vagy írd be a saját problémádat, és ellenőrizd a válaszodat a lépésről-lépésre történő magyarázatokkal.