
Galileót gyakran tartják a modern tudomány atyjának. Ő volt az, aki a kísérlet, az elmélet és a matematika alapelveit egységes keretbe foglalta. Valószínűleg mindenkinél jobban Galilei volt a felelős a modern tudomány fejlődéséért.
Azt mondják, hogy Galilei két különböző tömegű, de azonos anyagú acélgolyót dobott le a pisai ferde toronyról, és azok egyszerre értek földet. Ami figyelemre méltó ebben a kísérletben, az az, hogy ő vezette be a tudomány új módszerét, ahol kísérletet végeznek egy hipotézis tesztelésére. Megmutatta, hogy nem elég azt hinni, hogy valami igaz, hanem bizonyítani is kell.”

Galileo egy érdekes paradoxont talált, miközben a pisai egyetem matematikai tanszékének vezetője volt.
Meghatározás: A paradoxon, más néven antinómia, logikailag önmagának ellentmondó állítás vagy olyan állítás, amely ellentétes az ember várakozásával. (Wikipedia). (görög: “para” = túl, “doxa” = hit)
Galileo paradoxonja annak meghatározásáról szólt, hogy két végtelen tárgyakat tartalmazó halmaz egyenértékű-e egymással. Legyen például P a pozitív egész számok halmaza, ahol P= {0,1,2,3,…} és E a páros számok halmaza, ahol E = {0,2,4,6,…}. Galilei azt állította, hogy a két halmaz mérete azonos lesz, mert a P halmazból minden pozitív egész számot párosíthatunk az E halmaz páros számaival.

Hogyan lesz azonos a két halmaz mérete, ha E-ben egy “kevesebb” szám szerepel? Ezt Galilei-paradoxonnak nevezték el, és új vitát indított el a végtelen fogalmáról.
A Galilei után tanítványa, Evangelista Torricelli lett a pisai egyetem matematikai tanszékének vezetője. Talán a légköri nyomással kapcsolatos munkái és a barométer feltalálása miatt hallottál róla. Mivel Toricelli a matematika iránt is érdeklődik, felteszi a kérdést:
Lehet-e véges térfogatú és végtelen felületű tárgy? Először is, az ilyesmi a legtöbbünk számára valószínűtlennek tűnik. A matematika azonban azt mondja, hogy ilyesmi megtörténhet. Torricelli maga válaszolt a kérdésére, és felfedezte a Toricelli-trombitát, amelynek a felülete végtelen, de a térfogata véges. Felfedezését “hihetetlen” paradoxonnak tekintették.
Mellesleg van egy alapvető szabály a matematikafilozófiában; Bármelyik korszak filozófiájával vagy matematikájával foglalkozunk, az összefügg az adott terület történelmével, kultúrájával és vallásával. Ezért nevezik Toricelli trombitáját Gábriel kürtjének is. Azért történik itt utalás a Bibliára, mert a keresztények úgy hiszik, hogy az ítélet napján Gábriel angyal fújja meg a kürtöt.
Hogyan alakul Toricelli trombitája? Mindannyian tudjuk, hogyan kell az y=x grafikonját ábrázolni. Ha helyette az y=1/x egyenletet ábrázoljuk, ahol x nagyobb vagy egyenlő 1-nél, akkor a grafikon így néz ki:
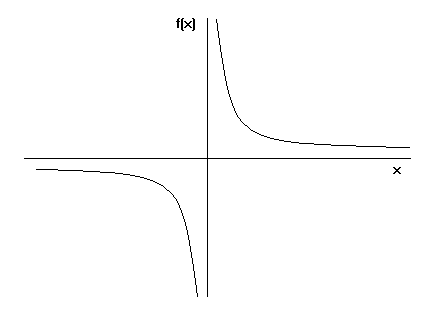
Ha fogjuk az y=1/x grafikonját, és elforgatjuk az x tengely körül, akkor Toricelli trombitáját látjuk.

Szerencsére matematikai képletek vannak a kezünkben, amelyekkel kiszámíthatjuk a Toricelli trombitájának területét és térfogatát. Amikor az alábbi integrációs képletet alkalmazzuk a trombita térfogatára, véges mennyiséget kapunk.
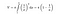
Ha azonban a trombita felületére az integrációs képletet alkalmazzuk, ezúttal végtelen lesz a trombita felülete. Hát nem érdekes ez az eredmény?
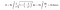
Mivel Toricelli trombitájának térfogata véges, véges mennyiségű festékkel tölthetjük meg. Tegyük fel például, hogy a térfogata 100 liter. Elmegyek a Home Depotba, veszek 100 liter festéket, és megtöltöm. Ez azonban attól lesz érdekes, hogy ezzel a 100 liter festékkel végtelen felületet fogok megfesteni. Ma ezt a paradoxont a legtöbben úgy hívják, hogy “festőparadoxon.”
Houston, van itt egy kis probléma! Az a helyzet, ami a gyakorlatban lehetetlen, a matematikában lehetségessé válik. Hogyan lehet tehát Torricelli trombitája valóságos? Vagy hogyan lehet pontosan megfeleltetni a halmazok összes elemét, miközben Galilei példájában az egyik halmaz egy másik részhalmaza?
Az összes ilyen konfliktus oka az, hogy a végtelen fogalma nem hasonlít más, általunk ismert fogalmakhoz, és ez sok embert összezavar. Galilei azt mondja a paradoxonjára,
“Igen, barátom, létezik a végtelen. Hiábavaló ellene tiltakozni. A halmazok, amelyekkel én foglalkozom, példák a zárt halmazokra, amelyek a végtelent tartalmazzák. Egy pontból indulnak ki, és a végtelenségig tartanak, és mégis, még mindig halmazok. A végtelenséggel kapcsolatos megjegyzéseimnek és fogalmaimnak azonban másnak kell lenniük, mint amiket a véges nagyságúakra használnék. Ha véges nagyságokkal foglalkozunk, akkor azt mondhatjuk, hogy 3 kiló kevesebb, mint 5 kiló, vagy 32 méter hosszabb, mint 7 méter. De amikor a végtelenről van szó, nem mondhatod, hogy ez a végtelen nagyobb, kisebb vagy egyenlő azzal.”
Ez volt Galilei megoldása az 1600-as években.
Sajnos Galilei megoldása új vitát indított el a végtelenségről. A matematikusok és filozófusok nem tudtak megegyezni egy konkrét válaszban, amíg Cantor meg nem osztotta “halmazelméletét”, amelyet a diákok ma már az általános iskolában tanulnak.
A végtelenség gondolatának fejlődését időszakosan historizálhatjuk. Először az eleatikusoknál jelent meg, amely egy Szókratész előtti filozófiai iskola volt, amelyet Parmenidész alapított az i. e. ötödik század elején az ókori Elea városában. Ennek az iskolának három nagy filozófusa volt: Zénón, Xenophanész és Parmenidész. Ebben az iskolában az volt az elfogadott filozófia, hogy a létezés szinguláris, és nincs többes szám. Zénón a végtelenséggel kapcsolatos paradoxonairól volt híres az eleatikusoknál. Később a Kr. e. 300-as években.., Arisztotelész felbukkant, és Zénón paradoxonjainak magyarázatára egy fogalompárt javasolt, amely a potenciális végtelenség és a tényleges végtelenség volt.
A potenciális végtelen a számok vagy “dolgok” olyan csoportja, amely vég nélkül folytatódik, folytatódik vagy ismétlődik újra és újra, felismerhető végpont nélkül.
A tényleges végtelen magában foglalja a soha véget nem érő halmazokat vagy “dolgokat” egy olyan téren belül, amelynek van kezdete és vége; ez egy olyan sorozat, amely technikailag “befejezett”, de végtelen számú tagból áll.
Aristotelész úgy vélte, hogy nincs tényleges végtelen. Arisztotelésznek ez az elképzelése egészen az 1600-as évekig uralta a filozófia világát. Ezután olyan filozófusok, mint Cusa és Bruno azt állították, hogy létezik tényleges végtelen, de nem tudjuk értelmezni. Cusa és Bruno után a nagy gondolkodó, Spinoza is bekapcsolódott a témába.
Spinoza azt mondta, hogy meg tudjuk érteni a végtelen fogalmát, és nagyság szerint rangsoroljuk őket. Ugyanakkor azt is kijelentette, hogy nem tudott matematikailag számolni velük. Például 3-at össze tudott adni 5-höz, de egyik végtelent a másikhoz nem tudta hozzáadni.
A viták lezárásaként végül megjelent egy gyönyörű ember, Georg Cantor, aki megalkotta a halmazelméletet, ami a mai napig a matematika alapja. Ő a halmazelméletével végleg pontot tett a végtelenséggel kapcsolatos vitákra.
Megmutatta, hogy egy végtelen halmaz nagyobb vagy kisebb lesz egy másik végtelen halmaznál. Továbbá Cantor azt állította, hogy összeadhatunk és szorozhatunk végtelen halmazokat. Addig az emberek Arisztotelész végtelenséggel kapcsolatos elképzeléseit követték. Arisztotelész szerint, ha a 3-as számot megszorozzuk a végtelennel, az ismét végtelen lesz. A végtelen mindent elnyelne. Ez alapján azt állította, hogy csak potenciális végtelen lenne, tényleges végtelen nem.
Kantor azonban a halmazelmélettel bebizonyította nekünk Arisztotelész elképzelésének az ellenkezőjét. Ha egy végtelen halmazhoz hozzáadunk egyet, az már nem lesz ugyanaz a halmaz. Megpróbálta összehasonlítani a végteleneket. Például Cantor bebizonyította, hogy az összes (0,1)→ℕ függvény halmaza megszámlálható. Így definiált egy-egy és onto függvényt a (0,1) intervallumból a természetes számokra.
Más szóval bebizonyította, hogy minden természetes szám belefér 0 és 1 közé, mert 0-1 között végtelen racionális számok voltak, és ezek a végtelenek párosíthatók. Ezután valami még veszélyesebbet tett, mint két egyenlő végtelenséget találni. Összehasonlította a valós számok végtelenjét a természetes számok végtelenjével, és megállapította, hogy a valós számok végtelenje nagyobb, mint a másik. Még a bizonyítását is megnézte, és azt mondta barátjának, Dedekindnek: “Látom, de még én sem tudom elhinni…”
Kantor is nagyon komoly filozófiai és vallási aggályokkal rendelkező matematikus volt. A halmazelmélet kidolgozása közben azt mondta: “Isten diktálta nekem a halmazelméletet.”
A halmazelmélet kidolgozása idején nem volt széles körben elfogadott. A vállalatok nem is alkalmazták Cantort semmilyen munkára. Egy matematikus, Henri Poincaré egyszer azt mondta: “Ennek a Cantornak az ötletei rossz betegség, amely a matematika gallérjára tapad. És a matematika egy nap majd meggyógyítja”. Cantornak egy időre elmegyógyintézetbe kellett mennie, és ott halt meg. Ma azonban zseninek tartjuk őt.
Cantor magányos ember volt a végtelen határán. A Transzfinit számokról szóló cikke elején a Bibliát idézte: “Minden, ami rejtve van, napvilágra kerül.”