A következőkben az interneten keringő, állítólag “common core matematika” vagy “új matematika” néhány matematikai problémájával foglalkozom. Úgy érzem, ezek a CCS téves megvalósítását mutatják be nekünk.

Ne feledjük, hogy nem minden, amit a matematikakönyvekben vagy az interneten látunk, a CCS alapján készült helyesen. A látott példák némelyikénél úgy tűnik, mintha az emberek a józan észt dobnák ki, amikor matematikai feladatokat készítenek a common core standardok szerint!”

Nem vagyok meglepve, hogy a végrehajtás néhány helyen “elfuserált” lett. A CCS a legtöbb tanár számára akkora változást jelent, hogy sok támogatásra és átképzésre van szükségük, mielőtt ezek szerint kell tanítaniuk.

Mindig is úgy gondoltam, hogy az állami iskolák általános iskolai matematikaoktatásának FŐ problémája az, hogy sok általános iskolai tanár nem érti eléggé a matematikát ahhoz, hogy még az általános iskolában is helyesen tudja tanítani. Például sokan közülük nem értik az általuk tanított algoritmusok fogalmait, miértjét és miértjét. Ez nem az ő hibájuk – a probléma arra vezethető vissza, amit a tanárképzésben és a saját iskolai tanulmányaik során tanítottak nekik.

Maga a szabványok dokumentuma is néhol kissé nehezen követhető. Elolvasása némi gondolkodást igényel. Bárcsak valaki készítene egy olyan füzetet, amely egyszerű nyelven és számos példával magyarázza el a standardokat.

Rossz példák a “közös magra” vagy az “új matematikára”

Példa 1

Nemrég a Facebookon láttam egy képet a kivonási stratégiákról, amely azt állította, hogy egy első osztályos matekkönyvből származik, és a “közös mag matematika”.”

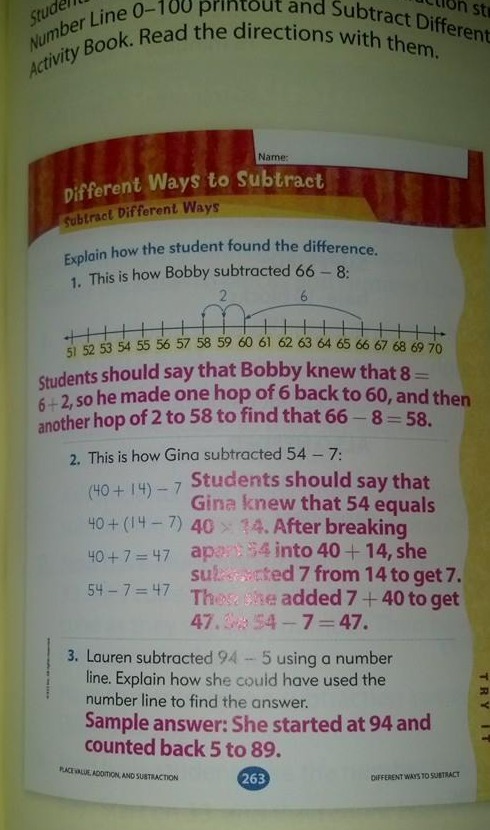
A 2. módszer szerintem túl nehéz az 1. osztály számára, és még az 1. módszert is meghagynám a 2. osztály számára.”

Az a könyv azonban úgy tűnik, hogy nem is igazodik a Common Core szabványokhoz. Az 1. osztályra vonatkozó szabványok egyszerűen nem tartalmaznak ilyen típusú kivonási feladatokat!

Ezt találjuk a szabványokban:

Összeadás és kivonás 20-on belül.
1.OA.5
Kapcsolja a számolást az összeadáshoz és a kivonáshoz (pl. 2-re számolva 2-t ad hozzá).
1.OA.6.
Adjunk és vonjunk ki 20-on belül, bizonyítva a 10-en belüli összeadás és kivonás folyékonyságát. Olyan stratégiák használata, mint a továbbszámolás; tízes számok alkotása (pl. 8 + 6 = 8 + 2 + 4 = 10 + 4 = 14); egy tízeshez vezető szám szétbontása (pl. 13 – 4 = 13 – 3 – 1 = 10 – 1 = 9); az összeadás és kivonás közötti kapcsolat használata (pl. tudva, hogy 8 + 4 = 12, tudja, hogy 12 – 8 = 4); és egyenértékű, de könnyebb vagy ismert összegek alkotása (pl., 6 +7 összeadása a 6 + 6 + 1 = 12 + 1 = 13 ismert egyenértékű összegek létrehozásával).

A tankönyvi példa úgy tűnik, hogy a fenti 1.OA.6. pontot akarja kezelni, de ez egyértelműen a 20-on belüli összeadásra és kivonásra vonatkozik, nem pedig a nagyobb számokra.

Az első osztályos standardokban később két standardot látunk, amelyek a kétjegyű számok kivonásával kapcsolatosak (100-on belül):

1.NBT.5.
Kétjegyű számot adva, gondolatban találj 10-tel többet vagy 10-tel kevesebbet a számnál, anélkül, hogy számolnod kellene; magyarázd meg az alkalmazott érvelést.
1.NBT.6.
Kivonja a 10-90-es tartományba tartozó 10 többszörösét a 10-90-es tartományba tartozó 10 többszöröséből (pozitív vagy nulla különbséggel), konkrét modellek vagy rajzok és a helyértékre, a műveletek tulajdonságaira és/vagy az összeadás és a kivonás közötti kapcsolatra épülő stratégiák segítségével; a stratégiát egy írott módszerhez kapcsolja, és magyarázza meg az alkalmazott érvelést.
Mária megjegyzése: ez olyan kivonásokat jelent, mint például 34 – 20 vagy 89 – 60.

de ezek egyike sem tartalmazza az olyan kivonásokat, mint az 54 – 7 vagy a 82 – 6. Ezek a 2. osztályban vannak:

2.NBT.5
Folyékonyan összeadni és kivonni 100-on belül a helyértékre, a műveletek tulajdonságaira és/vagy az összeadás és kivonás közötti kapcsolatra épülő stratégiák alkalmazásával.

Megjegyezzük, hogy a 2. osztályos standard nem határozza meg, HOGYAN vonszolsz ki (használsz-e mentális matematikai stratégiákat vagy számokat írsz egymás alá és kölcsönzöl/csoportosítasz).

Példa 2

A Houghton Mifflintől, állítólag:

Juanita matricás zacskókat akar adni a barátainak. Minden barátjának ugyanannyi matricát akar adni. Nem biztos benne, hogy 4 vagy 6 zacskó matricára van szüksége. Hány matricát vehetne úgy, hogy ne maradjon több matrica?

A matricás probléma a legkisebb közös többszörös (LCM) fogalmához kapcsolódik. (A válasz az, hogy 12, 24, 36 vagy 12 matricának bármely más többszörösét kell megvennie, mert akkor vagy 4 zacskóra vagy 6 zacskóra oszthatja őket.)

Naná, hogy a feladat NAGYON homályos és rosszul van megfogalmazva. Az a tippem, hogy a füzetben, amiben ez megjelenik, egyszerűen szerkesztetlen. Ez nem magának a szabványnak a hibája. Egyetértek Bart Goddarddal a Math Forumon. Ez annak a vak rohanásnak a tünete, hogy “életszerű” történeti problémákat akarnak gyártani, amelyek a végén értelmetlenek.

A PDF-dokumentumból, amelyben megjelenik, arra következtetek, hogy a feladat negyedik osztályosok számára készült, mivel a füzetben található összes többi szófeladat megfelel a 4. osztályra vonatkozó szabványoknak (tényezők, prímek). De a CCS még a legkisebb közös többszörösét sem tartalmazza a 4. osztályos standardokban (a 6. osztályban van)!!! Valami nagyon elromlott ezzel a szófeladattal.

3. példa

Még egyszer, állítólag a Houghton Mifflintől az 1. osztály számára. Ez megfelel a fentebb már idézett szabványnak:

Add and subtract within 20.
1.OA.6.
Add and subtract within 20, demonstrating fluency for addition andsubtraction within 10. Olyan stratégiák használata, mint a továbbszámolás; tízes számok alkotása (pl. 8 + 6 = 8 + 2 + 4 = 10 + 4 = 14); egy tízeshez vezető szám lebontása (pl. 13 – 4 = 13 – 3 – 1 = 10 – 1 = 9); az összeadás és a kivonás közötti kapcsolat használata (pl., tudva, hogy 8 + 4 = 12, tudjuk, hogy 12 – 8 = 4); és egyenértékű, de könnyebb vagy ismert összegek alkotása (pl. 6 +7 összeadása az ismert egyenértékű 6 + 6 + 1 = 12 + 1 = 13 alkotásával).

Most, először is, a “tízesedés” stratégiájának az ADDÍCIÓhoz van köze, nem a kivonáshoz. A kivonásnál ezt úgy hívják, hogy “tízhez vezető szám szétbontása”. Tehát az utasításnak azt kellene mondania: “Melyik mutatja a tízeshez vezető szám bontásának módját?”. Úgy érzem, hogy teljes képtelenség megkövetelni az első osztályosoktól, hogy ismerjék ezt a terminológiát.

De van itt egy másik probléma is. Ha valóban elolvassa az összes szabványt, akkor észreveheti, hogy számos más helyen arra kéri a tanulókat, hogy magyarázzák meg az alkalmazott érvelést, vagy hogy egy bizonyos vizuális módszert kapcsoljanak a stratégiához, de ebben a szabványban NEM!

Azt látom ebben a szabványban, hogy a tanároknak meg kell tanítaniuk az említett különböző stratégiákat, majd a tanulóknak egyszerű összeadási és kivonási feladatokat kell adniuk 20-on belül, például 15 – 8 és 10 – 6 feladatokat. NEM látom, hogy ez a szabvány megkövetelné a diákoktól, hogy felismerjék, hogy egy bizonyos vizuális modell megfelel-e egy bizonyos stratégiának.

Újra úgy tűnik, hogy a szerző elveti a józan észt… és valójában nem érti a szabványokat.

4. példa

A lenti példa nagyon rosszul van megfogalmazva, de a mögötte lévő KONCEPCIÓ nagyon jó, és a Math Mammothban is megtalálható. Ezért rá tudok jönni, hogy mit akarnak.

Öt négyzetet látsz. Színezz ki néhányat kékre, a többit pedig pirosra. Ez világos.

Majd színezd ki ugyanígy a négyzeteket a “számkötésben”. A számkötés ehhez a három körhöz tartozik. Az a gyermek, aki már volt olyan órán, ahol a tanár számkötést tanít, remélhetőleg tudja, mit jelent. Ez ugyanaz a koncepció, mint a ténycsalád… a felső szám az összeg vagy a végösszeg (5), és az alsó körökbe kerülő számok megfelelnek annak, hogy hányat színeztél kékre és hányat pirosra, ebben az esetben 1 és 4.

Azt hiszem, hogy a rejtett társak is az 1 és 4. Mutasd meg az 1 és 4 ujjadat egy felnőttnek. Végül színezd ki az 1 és 4 ujjat a képen (és ne a saját ujjaidat, mint ahogy ez hangzik).

Véleményem szerint az ujjakról szóló rész szuperflous és zavaró. Viszont a számkötés koncepciója sokkal régebbi, mint a CCS. A számkötések valójában nem szerepelnek a CCS-ben, bár kapcsolódnak ehhez a standardhoz:

1.OA.4
A kivonás ismeretlen-összetevő problémaként való megértése. Például 10 – 8 kivonása annak a számnak a megkeresésével, amely 8-hoz hozzáadva 10-et ad.

és ezzel

1.OA.6.
Adjunk és vonjunk ki 20-on belül, demonstrálva a 10-en belüli összeadás és kivonás folyékonyságát.

Nem tudom, miért van az a számkötéses feladatlap a Common Core Math példájaként megadva. Sokkal jobb lenne a rosszul megfogalmazott matematikai feladatlap példájaként megnevezni, amely akár a Common Core előtti időkből is származhat (és csak újra felhasználják ebben a konkrét tantervben)… mert mint mondtam, a számkötéseket NEM említi a CCS.

A Common Core Math Standards nem

1. Nem “új matematika”. A 2000-es években használt számos matematikai tantervhez képest, amelyek a nem hagyományos algoritmusokat hangsúlyozták, a CCS egyértelműen a hagyományos algoritmusok és a memorizálás felé mozdul el. Nézze meg ezeket a konkrét szabványokat:
   

   2.OA.2
   Folyékonyan összeadni és kivonni 20-on belül mentális stratégiák alkalmazásával. A 2. osztály végére emlékezetből ismerje két egyjegyű szám összes összegét.
   Maria megjegyzése: ezek az alapvető összeadási tények, mint például a 7 + 7 vagy az 5 + 4.

   3.OA.7
   Folyékonyan szoroz és oszt 100-on belül, olyan stratégiákat használva, mint a szorzás és osztás közötti kapcsolat (pl. tudva, hogy 8 × 5 = 40, tudjuk, hogy 40 ÷ 5 = 8) vagy a műveletek tulajdonságai. A 3. osztály végére emlékezetből ismerje két egyjegyű szám összes szorzatát.
   Maria megjegyzése: ez a szorzótáblákat és az alapvető osztási tényeket jelenti.

   4.NBT.4
   Folyamatosan összeadni és kivonni többjegyű egész számokat a standard algoritmus segítségével.

   5.NBT.5
   Folyamatosan szorozni többjegyű egész számokat a standard algoritmus segítségével.
   Maria megjegyzése: ez nem azt jelenti, hogy a tanulók csak 5. osztályban szoroznak többjegyű egész számokat; ezt 3. és 4. osztályban is tanulják.

2. A szabványok nem írnak elő furcsa stratégiákat vagy vizuális modelleket a tanárok és a diákok számára. Sok szabvány ezt a tanárokra és a diákokra bízza. Például:
   

   2.NBT.5
   Folyékonyan összeadni és kivonni 100-on belül a helyértékeken, a műveletek tulajdonságain és/vagy az összeadás és kivonás közötti kapcsolaton alapuló stratégiák alkalmazásával.

   Figyeljünk a “és/vagy”-re a fenti mondatban. Ez azt jelenti, hogy a tanárok és a tanulók NEM korlátozódnak semmilyen konkrét stratégia használatára, és NEM utasítják őket több stratégia használatára. A hagyományos “kölcsönzés” algoritmus egy helyértékre épülő stratégia, ezért itt szerepel a 2.NBT.5. pontban.

   2.NBT.9
   Magyarázza meg, miért működnek az összeadási és kivonási stratégiák a helyérték és a műveletek tulajdonságainak felhasználásával. A magyarázatokat rajzokkal vagy tárgyakkal lehet alátámasztani.

   Az állítás szerint “rajzokkal lehet alátámasztani”, de nem kényszerít erre, és nem korlátozza egy adott vizuális modell vagy rajztípus használatára.

   3.OA.3.
   A 100-on belüli szorzást és osztást alkalmazza az egyenlő csoportokat, tömböket és mérőmennyiségeket tartalmazó szófeladatok megoldására, pl. rajzok és egyenletek segítségével, az ismeretlen szám szimbólumával a probléma ábrázolásához.

   A tanulónak nem KELL rajzot használnia. Ez csak lehetőségként szerepel.

   4.NBT.5
   Megszorozni egy legfeljebb négyjegyű egész számot egy egyjegyű egész számmal, és megszorozni két kétjegyű számot, a helyértékeken és a műveletek tulajdonságain alapuló stratégiák alkalmazásával. Illusztrálja és magyarázza a számítást egyenletek, négyszögletes tömbök és/vagy areamodellek segítségével.

   Figyeljen a “és/vagy” szóra. Illusztrálja a számítást, de elég, ha egyenletekkel szemlélteti. Nem KÖTELEZŐ tömbökkel szemléltetni.

   Ezzel együtt néhány szabvány említ konkrét vizuális modellt, például számvonalat vagy téglalap alakú területmodellt, de ez ritkább, mintha választási lehetőséget adnánk, mint a fenti szabványokban.

Fogalmi matematika

Vannak olyan standardok, amelyek a matematika fogalmi oldalát érintik, amelyeket az általános iskolai tanárok nem biztos, hogy megértenek, ha nem tanítják meg nekik, hogy mit jelentenek; például:

5. NF.7b
Egy egész szám egységnyi törttel való osztásának értelmezése, és az ilyen hányadosok kiszámítása. Például készítsen történeti összefüggést a 4 ÷ (1/5) osztáshoz, és használjon vizuális törtmodellt a hányados ábrázolásához. Használja a szorzás és osztás közötti összefüggést, hogy elmagyarázza, hogy 4 ÷ (1/5) = 20, mert 20 × (1/5) = 4.

Egy ilyen történeti feladat lehet: hány 1/5 láb hosszú darabot tudsz kivágni egy 4 láb hosszú anyagdarabból? Egy vizuális modell mutathatna 4 egészet, ötödrészekre osztva. Ezután megszámolhatjuk, hogy 4 egésznek összesen 20 ötöde van.

5.NF.4b
Következtessük egy tört oldalhosszúságú téglalap területét úgy, hogy azt a megfelelő tört oldalhosszúságú egységnyi négyzetekkel burkoljuk, és mutassuk meg, hogy a terület megegyezik azzal, amit az oldalhosszúságok szorzatával kapnánk. Szorozzuk meg a tört oldalhosszúságokat, hogy megtaláljuk a derékszögek területét, és ábrázoljuk a törtek termékét téglalap területként.

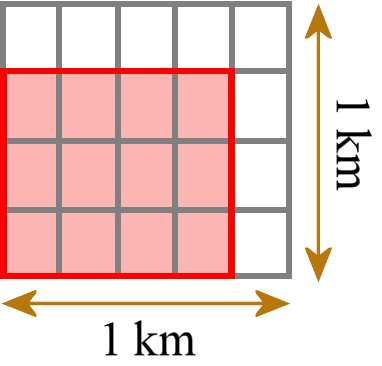Ez például egy 3/4 km és 4/5 km oldalhosszúságú téglalapot jelent. Ezután ezt kis egységnyi téglalapokkal (nem egységnyi négyzetekkel; itt maga a szabvány használja a rossz terminológiát) csempézzük, amelyeknek egyenként 1/4 km és 1/5 km oldalhosszúságúak.

Megszámolhatjuk, hogy hány kis csempére van szükségünk. Nekünk 12 ilyen lapkára van szükségünk. Minden egyes lapkának 1/20 km2 a területe, tehát a teljes terület 12/20 km2. Ezután ellenőrizzük és összehasonlítjuk, hogy ugyanazt a választ kapjuk, mintha a két oldalhosszúságot rendes tört szorzással szoroztuk volna meg (3/4 km × 4/5 km = 12/20 km2).

Mindig is voltak ilyen jellegű feladatok a könyveimben – még a CCS megjelenése előtt is.

Mások azzal érvelnek, hogy a gyerekeknek nincs szükségük ilyen fogalmi megértésre, vagy hogy ez túl nehéz. Én személy szerint nem értek ezzel egyet. Mindig (a CCS előtt is) arra törekedtem, hogy a törtaritmetika fogalmait úgy magyarázzam el, hogy a tanulók ne “vakon kövessék a szabályokat”, és csak akkor tudjanak törtekkel számolni, ha történetesen helyesen emlékeznek a szabályra. Mindig is a fogalmi megértést hangsúlyoztam a matematikában (mint olvasóim tudják!).”

De remélem, érthető, hogy ezek közül néhány dolog ismeretlen lehet az iskolai tanárok és a szülők számára, és ezért nem csoda, hogy a Common Core Standards követése nehézséget okoz számukra.

Az a reményem, hogy a Math Mammoth Light Blue sorozat és a Teachers Pay Teachers és Teachers’ Notebook boltjaimban árult egységeim segíthetnek azoknak a tanároknak & szülőknek, akiknek a Common Core-hoz igazodó anyagokra van szükségük. És ahogy mondtam, a többiek is bátran használhatják őket. Nem tartalmaznak semmilyen “furcsa” vagy értelmetlen matematikát, hanem mint mindig, egyszerűen a matematikai fogalmak tanításának szilárd alapjára épülnek az eljárásokkal együtt.

Maria Miller

által.