Představte si čtverec papíru, který leží rovně na vašem stole. Požádám vás, abyste zavřeli oči. Uslyšíte, jak se papír posouvá. Když oči otevřete, zdá se, že se papír nezměnil. Co jsem s ním mohl udělat, zatímco jste se nedívali?“
Je zřejmé, že jsem papír neotočil o 30 stupňů, protože pak by papír vypadal jinak.

Také jsem ho nepřevrátil přes čáru spojující například jeden z rohů se středem jiné hrany. Kdybych tak učinil, papír by vypadal jinak.

Mohl jsem však papír otočit ve směru nebo proti směru hodinových ručiček o libovolný násobek 90 stupňů nebo jej převrátit přes některou z diagonálních čar nebo vodorovnou a svislou čáru.
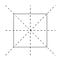
Pomocí pro vizualizaci transformací je označení rohů čtverce.

Poslední možností je, že neuděláte nic. Tomu se říká transformace identity. Všechny tyto transformace dohromady se nazývají symetrické transformace čtverce.
Symetrické transformace mohu kombinovat a vytvářet tak další symetrické transformace. Například dvě převrácení přes úsečku BD vytvoří identitu, stejně jako čtyři po sobě jdoucí otočení o 90 stupňů proti směru hodinových ručiček. Převrácení kolem svislé přímky následované převrácením kolem vodorovné přímky má bezpečný účinek jako otočení o 180 stupňů. Obecně platí, že jakákoli kombinace symetrických transformací vytvoří symetrickou transformaci. Následující tabulka uvádí pravidla pro skládání symetrických transformací:

V této tabulce R s indexy 90, 180 a 270 označují otočení proti směru hodinových ručiček o 90, 180 a 270 stupňů, H znamená otočení kolem vodorovné přímky, V je otočení kolem svislé přímky, MD je otočení kolem úhlopříčky zleva nahoru doprava dolů a OD znamená otočení přes druhou úhlopříčku. Chcete-li zjistit součin A a B, přejděte na řádek A a poté na sloupec B. Například H∘MD=R₉₀.
Při pohledu na tabulku si můžete všimnout několika věcí:
- Operace ∘ je asociativní, což znamená, že A∘(B∘C) = (A∘B)∘C pro libovolné transformace A, B a C. A∘(B∘C) = (B∘C).
- Pro každou dvojici symetrických transformací A a B je kompozice A∘B také symetrickou transformací
- Existuje jeden prvek e takový, že A∘e=e∘A pro každou A
- Pro každou symetrickou transformaci A, existuje jedinečná symetrická transformace A-¹ taková, že A∘A-¹=A-¹∘A=e
Říkáme tedy, že množina symetrických transformací čtverce spolu s kompozicí tvoří matematickou strukturu zvanou grupa. Tato grupa se nazývá D₄, dihedrální grupa pro čtverec. Tyto struktury jsou předmětem tohoto článku.
Definice grupy
Grupa ⟨G,*⟩ je množina G s pravidlem * pro kombinaci libovolných dvou prvků v G, které splňuje grupové axiomy:
V abstraktu často potlačujeme * a píšeme a*b jako ab a * označujeme jako násobení.

Není nutné, aby * bylo komutativní, což znamená, že a*b=b*a. Proto je nutné, aby * bylo komutativní. Můžete se o tom přesvědčit, když se podíváte na tabulku D₄, kde H∘MD=R₉₀, ale MD∘H=R₂₇₀. Skupiny, kde je * komutativní, se nazývají abelovské grupy podle Neilse Abela.
Abelovské grupy jsou spíše výjimkou než pravidlem. Dalším příkladem neabelovské grupy jsou symetrické transformace krychle. Uvažujme jen rotace kolem os:
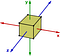

Je možné, aby prvek byl svou vlastní inverzí. Uvažujme grupu, která se skládá z 0 a 1 s operací binárního sčítání. Její tabulka je:

Je jasné, že 1 je svou vlastní inverzí. To je také abelická grupa. Nebojte se, většina grup není tak nudná.
Mezi další příklady grup patří:
- Množina celých čísel se sčítáním.
- Množina racionálních čísel neobsahujících 0 s násobením.
- Množina řešení polynomiální rovnice xⁿ-1=0, zvaná n-té kořeny jednoty, s násobením.
Uvedeme několik příkladů, které nejsou grupami:
- Množina přirozených čísel při sčítání není grupou, protože neexistují její inverze, což by byla záporná čísla.
- Množina všech racionálních čísel včetně 0 s násobením není grupa, protože neexistuje žádné racionální číslo q, pro které by 0/q=1, takže ne každý prvek má inverzi.
Struktura grupy
Grupa je mnohem víc než jen kapka, která splňuje čtyři axiomy. Grupa může mít vnitřní strukturu a tato struktura může být velmi složitá. Jedním ze základních problémů abstraktní algebry je určit, jak vypadá vnitřní struktura grupy, protože v reálném světě jsou skutečně studované grupy mnohem větší a složitější než jednoduché příklady, které jsme zde uvedli.
Jedním ze základních typů vnitřní struktury je podgrupa. Grupa G má podgrupu H, když H je podmnožinou G a:
- Pro a,b∈H, a*b∈H a b*a∈H
- Pro a∈H, a-¹∈H
- Totožnost je prvkem H
Jestliže H≠G, pak se říká, že H je vlastní podgrupa. Podgrupa G tvořená pouze identitou se nazývá triviální podgrupa.
Neabelová grupa může mít komutativní podgrupy. Uvažujme čtvercovou dihedrální grupu, o které jsme hovořili v úvodu. Tato grupa není abelická, ale podgrupa rotací je abelická a cyklická:
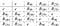
Nyní uvedeme dva příklady struktury grupy.
I když grupa G není abelická, přesto může platit, že existuje množina prvků G, které komutují se vším v G. Tato množina se nazývá střed G. Střed C je podgrupa G. Důkaz:
Předpokládejme nyní, že f je funkce, jejíž obor i rozsah je G. Perioda f je prvek a∈G takový, že f(x)=f(ax) pro všechna x∈G. Množina P period f je podgrupa G. Důkaz:
Konečné grupy jsou konečně generované
Viděli jsme, že cyklické grupy jsou generovány jediným prvkem. Když je možné každý prvek grupy G zapsat jako součin (ne nutně vlastní) podmnožiny A grupy G, pak říkáme, že A generuje G a zapisujeme to jako G=⟨A⟩. Nejvíce „no, duh“ důkaz, který kdy uvidíte, je důkaz, že všechny konečné grupy jsou generovány konečnou generující množinou:
- Nechť G je konečná. Každý prvek G je součinem dvou jiných prvků G, takže G=⟨G⟩. QED.

Tento článek zakončíme aplikací.
Komunikace odolná proti chybám
Nejjednodušší způsob přenosu digitální informace je zakódovat ji do binárních řetězců pevné délky. Žádné komunikační schéma není zcela bez rušení, takže vždy existuje možnost, že budou přijata nesprávná data. Metoda dekódování s maximální pravděpodobností je jednoduchý a účinný přístup k detekci a opravě chyb při přenosu.
Nechť 𝔹ⁿ je množina binárních řetězců neboli slov délky n. Je jednoduché ukázat, že 𝔹ⁿ je abelická grupa při binárním sčítání bez přenášení (takže například 010+011=001). Všimněte si, že každý prvek je svou vlastní inverzí. Kód C je podmnožinou 𝔹ⁿ. Následuje příklad kódu v 𝔹⁶:
C = {000000, 001011, 010110, 011101, 100101, 101110, 110011, 111000}
Prvky kódu se nazývají kódová slova. Přenášena budou pouze kódová slova. O chybě se hovoří, když rušení změní bit v přenášeném slově. Vzdálenost d(a,b) mezi dvěma kódovými slovy a a b je počet číslic, ve kterých se dvě kódová slova liší. Minimální vzdálenost kódu je nejmenší vzdálenost mezi libovolnými dvěma jeho kódovými slovy. Pro právě uvedený příklad kódu je minimální vzdálenost tři.
Při metodě dekódování s maximální pravděpodobností, pokud obdržíme slovo x, které může obsahovat chyby, by měl příjemce interpretovat x jako kódové slovo a tak, že d(a,x) je minimální. Ukážu, že pro kód s minimální vzdáleností m lze tímto způsobem vždy (1) odhalit chyby, které mění méně než m bitů, a (2) opravit chyby, které mění ½(m-1) nebo méně bitů.

V našem příkladu kódu je m=3 a koule o poloměru ½(m-1)=1 kolem kódového slova 011101 je {011101, 111101, 001101, 011001, 010101, 011111, 011100}. Pokud tedy příjemce přijme některé z těchto slov, ví, že měl přijmout 011101.
Tak to je všechno hezké, ale co to má společného s teorií grup? Odpověď je v tom, jak vlastně vytváříme kódy, s nimiž tato metoda pracuje.
Je možné, aby kód v 𝔹ⁿ tvořil podgrupu. V takovém případě říkáme, že kód je skupinovým kódem. Skupinové kódy jsou konečné grupy, takže jsou konečně generované. Uvidíme, jak kód vytvořit nalezením generující množiny.
Kód lze zadat tak, že prvních několik bitů každého kódového slova se nazývá informační bity a bity na konci se nazývají paritní bity. V našem příkladu kódu C jsou první tři bity informační bity a poslední tři bity jsou paritní bity. Paritní bity splňují rovnice paritní kontroly. Pro kódové slovo A₁A₂A₃A₄A₅A₆ jsou rovnice parity následující: A₄=A₁+A₂, A₅=A₂+A₃ a A₆=A₁+A₃. Paritní rovnice poskytují další vrstvu ochrany proti chybám: pokud některá z paritních rovnic není splněna, pak došlo k chybě.
Takto postupujeme. Předpokládejme, že chceme kódová slova s m informačními bity a n paritními bity. Pro vytvoření skupinového kódu napíšeme matici s m řádky a m+n sloupci. Do bloku tvořeného prvními m sloupci zapište identitní matici m×m. Do sloupce j pro m+1≤j≤m_n zapište do k-tého řádku jedničku, pokud se v paritní rovnici pro paritní bit Aₖ objeví Aⱼ, a jinak 0. V našem příkladu kódu je matice:

Taková matice se nazývá generující matice pro skupinový kód. Lze přímo ověřit, že řádky generují C:

Řádky libovolné generující matice tvoří generující množinu pro grupový kód C. Důkaz:
- Identita a inverze:
- Závěr: Jestliže A,B∈C, pak A a B jsou součty řádků generující matice, takže A+B je také součtem řádků generující matice. Proto A+B∈C.
To nám umožňuje generovat kód, nyní ukážu, jak vygenerovat užitečný kód.
Zdefinujte váhu w(x), která znamená počet jedniček v x. Například w(100101)=3. Je zřejmé, že w(x)=d(x,0), kde 0 je slovo, jehož všechny číslice jsou nuly. Minimální váha W kódu je váha nenulového kódového slova s nejmenším počtem jedniček v kódu. Pro kód s minimální vzdáleností m platí d(x,0)≥m, takže w(x)≥m, a proto W=m.
Připomeňme, že aby slovo mohlo být považováno za kódové slovo, musí splňovat soubor rovnic kontroly parity. Pro náš příklad kódu jsou to A₄=A₁+A₂, A₅=A₂+A₃ a A₆=A₁+A₃. Můžeme je také zapsat jako lineární soustavu:
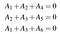
Kterou samotnou můžeme zapsat v podobě bodových součinů:

Nebo v kompaktnějším tvaru jako Ha=0 kde a=(A₁,A₂,A₃,A₄,A₅,A₆) a H je matice kontroly parity kódu:

Přímým výpočtem lze ověřit, že pokud w(a)≤2, pak nemůžeme mít Ha=0. Obecně platí, že minimální váha je t+1, kde t je nejmenší takové číslo, že libovolná množina t sloupců H se nesčítá s nulou (tj. jsou lineárně nezávislé). Dokazování tohoto faktu by nás zavedlo až příliš daleko do lineární algebry.
Pokud vás to děsí, nebojte se. Můžeme vytvořit několik velmi dobrých kódů i bez toho, když využijeme toho, že z výsledku, který jsem právě zmínil, vyplývá, že pokud je každý sloupec H nenulový a žádné dva sloupce se nerovnají, pak je minimální váha, a tedy i minimální vzdálenost kódu, alespoň tři. To je velmi dobré: Jestliže se v našem komunikačním systému očekává jedna bitová chyba na každých sto přenesených slov, pak pouze jedno z deseti tisíc přenesených slov bude mít neopravenou chybu a jedno z milionu přenesených slov bude mít nezjištěnou chybu.
Takže nyní máme recept na výrobu užitečného kódu pro schéma detekce maximální pravděpodobnosti pro kódová slova obsahující m informačních bitů a n paritních bitů:
- Vytvořte matici s m+n sloupci a n řádky. Vyplňte matici jedničkami a nulami tak, aby žádné dva sloupce nebyly stejné a žádný sloupec nebyl pouze nulový.
- Každý řádek výsledné matice kontroly parity odpovídá jedné z rovnic paritních bitů. Zapište je jako soustavu rovnic a vyřešte tak, aby každý paritní bit byl zapsán ve smyslu informačních bitů.
- Vytvořte matici o m+n sloupcích a m řádcích. Do bloku tvořeného prvními m sloupci zapište matici identity m×m. Do sloupce j pro m+1≤j≤m_n zapište do k-tého řádku 1, pokud se v paritní rovnici pro paritní bit Aₖ vyskytuje Aⱼ, a jinak 0.
- Řádky této matice jsou generátory kódové skupiny s minimální vzdáleností alespoň tři. To je kód, který budeme používat.
Předpokládejme, že potřebuji jednoduchý osmislovný kód a potřebuji pouze základní detekci chyb, nikoliv jejich opravu, takže si vystačím s minimální vzdáleností dva. Chci tři informační bity a dva paritní bity. Zapíšu si následující matici kontroly parity:
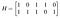
Dvě dvojice sloupců jsou si rovny, takže nejmenší t, pro které je libovolná kolekce t sloupců lineárně nezávislá, je jedna, takže minimální váha, a tedy minimální vzdálenost, kterou budu mít, je dvě. Řádky představují rovnice kontroly parity A₄=A₁+A₃ a A₅=A₁+A₂+A₃. Moje generující matice je tedy:

A řádky této matice generují skupinu kódů:
- {00000, 00111, 01001, 01110, 10011, 10100, 111010, 11101}
Závěrečné poznámky
Abstraktní algebra je hluboké téma s dalekosáhlými důsledky, které se však také velmi snadno učí. Kromě několika letmých zmínek o lineární algebře je téměř vše, co jsem zde probíral, přístupné i někomu, kdo má za sebou pouze středoškolskou algebru.
Když mě poprvé napadlo napsat tento článek, opravdu jsem chtěl mluvit o Rubikově kostce, ale nakonec jsem chtěl vybrat příklad, který by se dal obsáhnout jen pomocí nejzákladnějších myšlenek z teorie grup. Navíc o grupě Rubikovy kostky se toho dá říct tolik, že by si zasloužila samostatný článek, takže se ho brzy dočkáme.
Moje vysokoškolské kurzy abstraktní algebry byly založeny na knize A Book of Abstract Algebra od Charlese Pintera, což je přístupné zpracování. Všechny příklady v tomto článku byly s určitými úpravami převzaty od Pintera.
Na závěr dodávám, že všechny obrázky, které nejsou citovány, jsou mým původním dílem a mohou být použity s uvedením autora. Jako vždy ocením jakékoli opravy nebo žádosti o vysvětlení.