Cíle výuky
- Pochopit 3D zobrazení elektronických orbitalů
Orbital je kvantově mechanické zpřesnění Bohrova orbitu. Na rozdíl od jeho koncepce jednoduché kruhové\(r\) orbity s pevným poloměrem jsou orbitaly matematicky odvozené oblasti prostoru s různou pravděpodobností, že obsahují elektron.
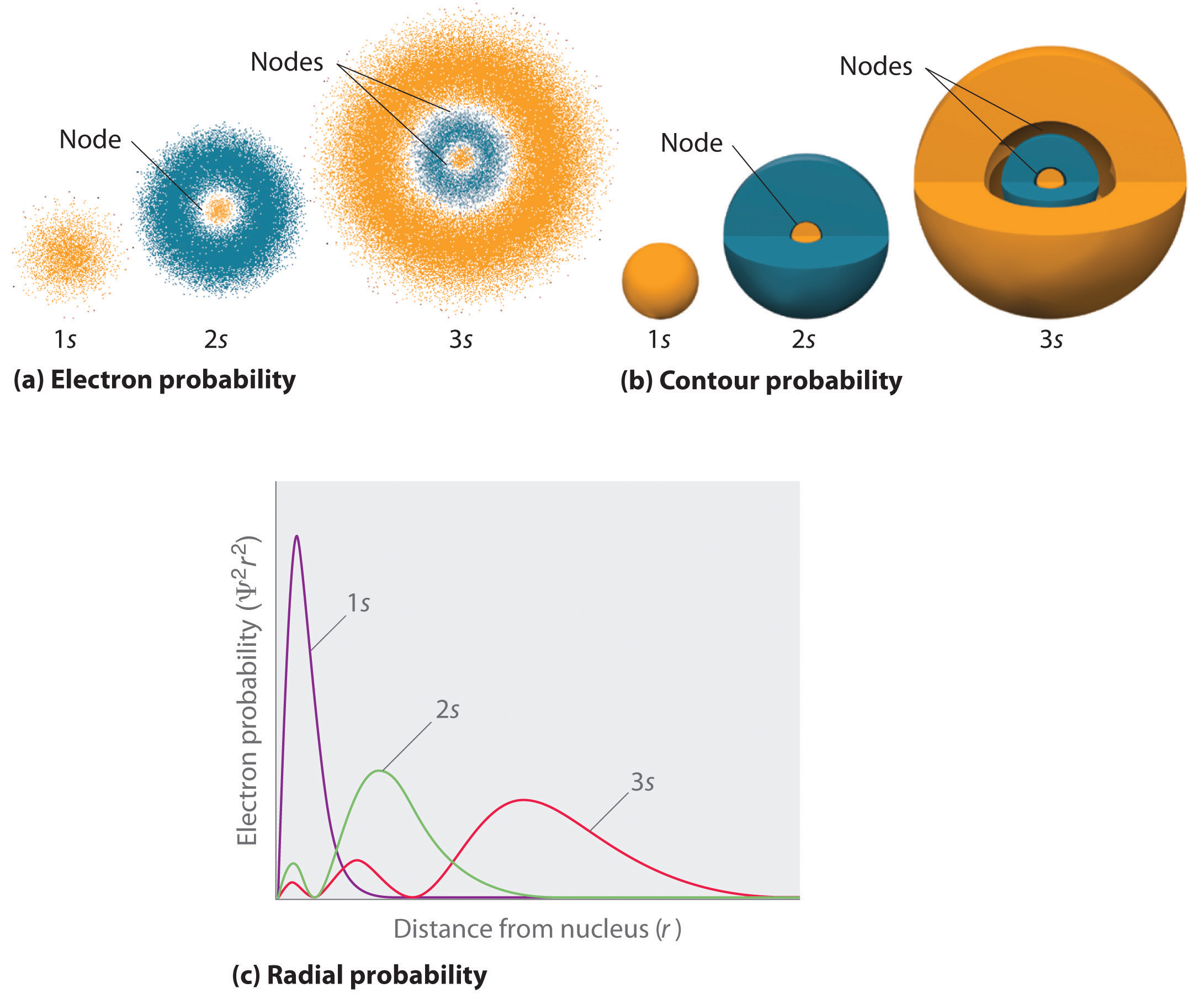
Jeden způsob reprezentace rozdělení pravděpodobnosti elektronů byl dříve ilustrován fo\(r\) 1s orbitalu vodíku. Protože Ψ2 udává pravděpodobnost nalezení elektronu v daném objemu prostoru (např. kubický pikometr), je graf závislosti Ψ2 na vzdálenosti od jádra (r) grafem hustoty pravděpodobnosti. Orbital 1s je sféricky symetrický, takže pravděpodobnost nalezení elektronu 1s v daném bodě závisí pouze na jeho vzdálenosti od jádra. Hustota pravděpodobnosti je největší v bodě \(\(r\) = 0\). (u jádra) a s rostoucí vzdáleností neustále klesá. Při velmi velkých hodnotách r je hustota pravděpodobnosti elektronu velmi malá, ale není nulová.
Naproti tomu můžeme vypočítat radiální pravděpodobnost (pravděpodobnost nalezení 1s elektronu ve vzdálenosti \(r\) od jádra) sečtením\(r\) pravděpodobností, že se elektron nachází ve všech bodech řady x kulových slupek o poloměru r1, r2, r3,…, rx – 1, rx. V podstatě rozdělíme atom na velmi tenké soustředné slupky, podobně jako vrstvy cibule (obrázek \(\PageIndex{1a}\)), a vypočítáme pravděpodobnost, že se elektron nachází na každé kulové slupce. Připomeňme, že hustota pravděpodobnosti elektronů je největší v bodě \(r\) = 0 (obrázek \(\PageIndex{1b}\), takže hustota bodů je největší v nejmenších kulových slupkách v části (a) na obrázku \(\PageIndex{1}\). Naproti tomu plocha povrchu každé kulové skořápky je rovna \(4πr^2\), která se velmi rychle zvětšuje s rostoucím \(r\) (obrázek \(\PageIndex{1c}\)). Protože povrch kulových slupek se s rostoucím \(r\) zvětšuje rychleji, než klesá hustota pravděpodobnosti elektronů, má graf radiální pravděpodobnosti maximum v určité vzdálenosti \(r\) (obrázek \(\PageIndex{1d}\). Nejdůležitější je, že když je \(r\) velmi malé, je povrch kulového obalu tak malý, že celková pravděpodobnost nalezení elektronu v blízkosti jádra je velmi nízká; u jádra pravděpodobnost elektronu mizí (obrázek \(\PageIndex{1d}\)).

Fo\(r\) atomu vodíku, vrchol v grafu radiální pravděpodobnosti nastává při \(r\) = 0,529 Å (52,9 pm), což je přesně poloměr vypočtený Bohrovým modelem fo\(r\) n = 1 orbity. Nejpravděpodobnější poloměr získaný z kvantové mechaniky je tedy totožný s poloměrem vypočteným klasickou mechanikou. V Bohrově modelu se však předpokládalo, že elektron je v této vzdálenosti 100 % času, zatímco ve Schrödingově modelu je v této vzdálenosti jen po určitou dobu. Rozdíl mezi oběma modely je dán vlnovým chováním elektronu a Heisenbergovým principem neurčitosti.
Obrázek \(\PageIndex{2}\) porovnává hustoty pravděpodobnosti elektronů na 1s, 2s a 3s orbitu vodíku. Všimněte si, že všechny tři jsou sféricky symetrické. U orbitalů 2s a 3s (a také u všech ostatních orbitalů s) však pravděpodobnostní hustota elektronů neklesá plynule s rostoucí hodnotou \(r\). Místo toho je na grafech radiální pravděpodobnosti pozorována řada minim a maxim (obrázek \(\PageIndex{2c}\)). Minima odpovídají kulovým uzlům (oblastem s nulovou pravděpodobností elektronů), které se střídají s kulovými oblastmi s nenulovou pravděpodobností elektronů. Existence těchto uzlů je důsledkem změn vlnové fáze ve vlnové funkci Ψ.
Orbitaly s (l=0)
S rostoucím n se s orbitaly dějí tři věci (obrázek \(\PageIndex{2}\)):
- Zvětšují se a sahají dále\(r\) od jádra.
- Obsahují více uzlů. To je podobné jako u stojaté vlny, která má oblasti se značnou amplitudou oddělené uzly, body s nulovou amplitudou.
- V daném atomu mají orbitaly s s rostoucím n také vyšší energii, protože se zvětšuje jejich vzdálenost od jádra.
Orbitaly se obvykle kreslí jako trojrozměrné plochy, které uzavírají 90 % elektronové hustoty, jak bylo ukázáno u 1s, 2s a 3s orbitalů vodíku v části b) na obrázku \(\PageIndex{2}\). Ačkoli tyto nákresy ukazují relativní velikosti orbitalů, obvykle nezobrazují sférické uzly v orbitalech 2s a 3s, protože sférické uzly leží uvnitř 90% povrchu. Poloha sférických uzlů naštěstí není důležitá fo\(r\) chemické vazby.
p Orbitaly (l=1)
Pouze s orbitaly jsou sféricky symetrické. S rostoucí hodnotou l roste počet\(r\) orbitalů v dané podskupině a tvary orbitalů se stávají složitějšími. Protože podpouzdro 2p má l = 1 a tři hodnoty ml (-1, 0 a +1), existují tři orbitaly 2p.
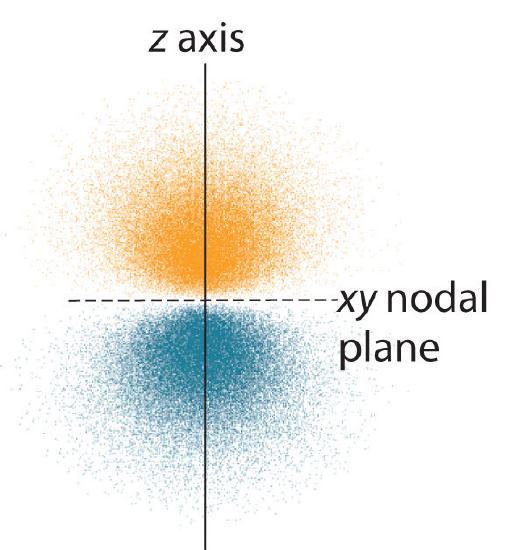
Rozdělení pravděpodobnosti elektronů fo\(r\) jednoho z 2p orbitalů vodíku je znázorněno na obrázku \(\PageIndex{3}\). Protože tento orbital má dva laloky elektronové hustoty uspořádané podél osy z s nulovou elektronovou hustotou v rovině xy (tj. rovina xy je uzlovou rovinou), jedná se o orbital \(2p_z\). Jak je znázorněno na obrázku \(\PageIndex{4}\), další dva 2p orbitaly mají stejný tvar, ale leží podél osy x (\(2p_x\)) a y (\(2p_y\)). Všimněte si, že každý p orbital má pouze jednu uzlovou rovinu. V každém případě je fáze vlnové funkce fo\(r\) každého z 2p orbitalů kladná fo\(r\) laloku, který směřuje podél kladné osy, a záporná fo\(r\) laloku, který směřuje podél záporné osy. Je důležité zdůraznit, že tato znaménka odpovídají fázi vlny, která popisuje pohyb elektronů, nikoli kladným o\(r\) záporným nábojům.
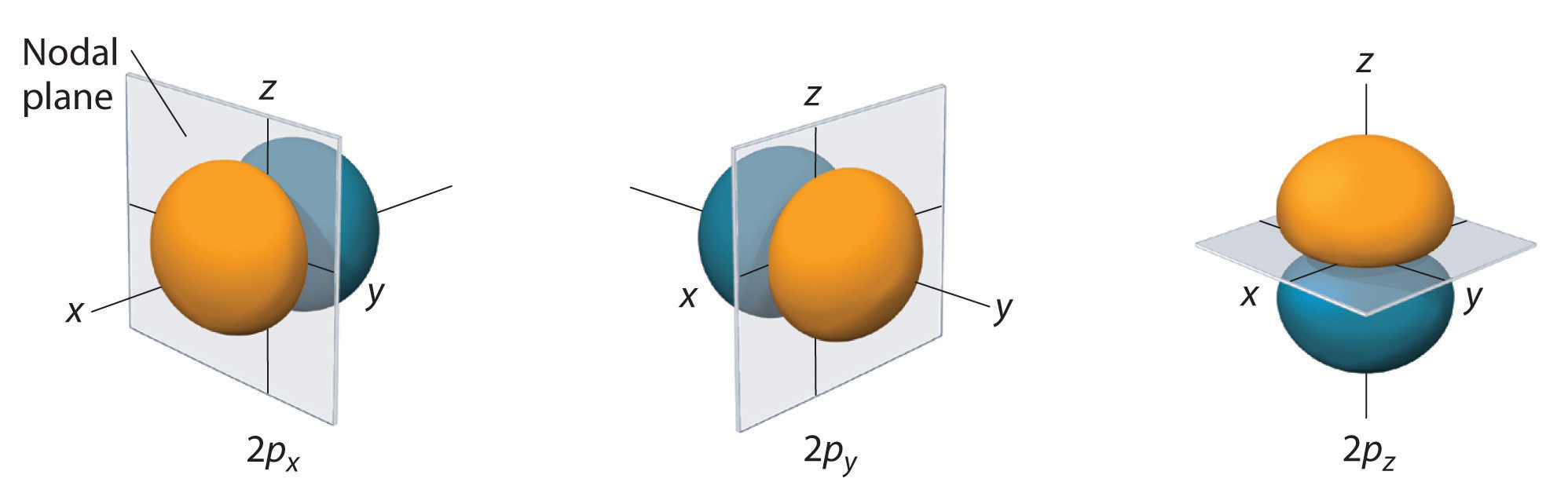
Zobrazené plochy uzavírají 90% celkové pravděpodobnosti elektronů fo\(r\) orbitalů 2px, 2py a 2pz. Každý orbital je orientován podél osy označené indexem a uzelná rovina kolmá\(r\) k této ose protíná každý 2p orbital. Fáze vlnové funkce je kladná (oranžová) v oblasti prostoru, kde x, y, o\(r\) z je kladná, a záporná (modrá) tam, kde x, y, o\(r\) z je záporná. Stejně jako u s orbitalů se velikost a složitost p orbitalů fo\(r\) každého atomu zvětšuje s rostoucím hlavním kvantovým číslem n. Tvary 90% pravděpodobnostních ploch orbitalů 3p, 4p a p s vyšší energií jsou však v podstatě stejné jako na obrázku \(\PageIndex{4}\).
d Orbitaly (l=2)
Podslupky s l = 2 mají pět d orbitalů; první hlavní slupka, která má d podslupku, odpovídá n = 3. Pět d orbitalů má ml hodnoty -2, -1, 0, +1 a +2.
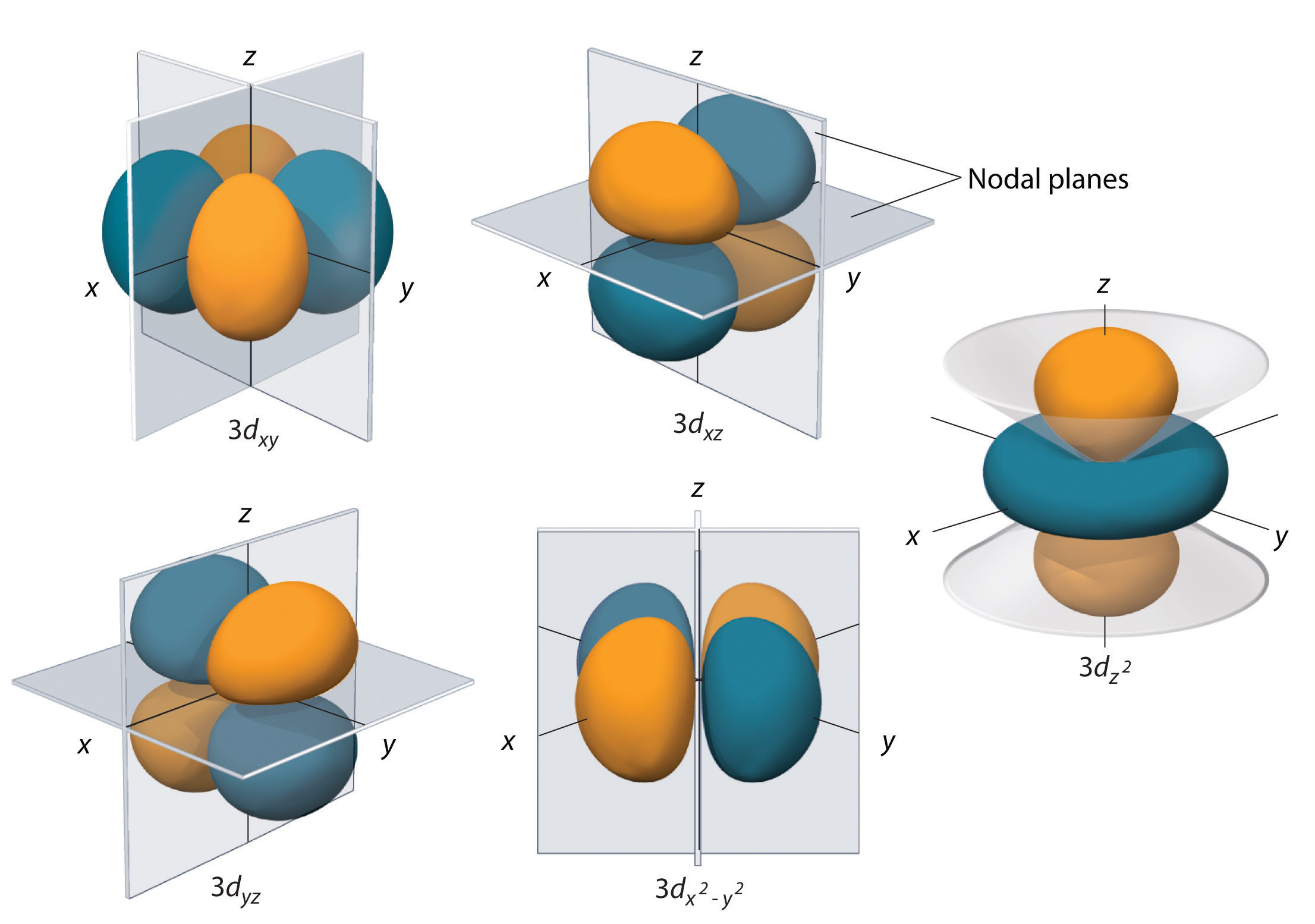
Vodíkové 3d orbitaly, zobrazené na obrázku \(\PageIndex{5}\), mají složitější tvary než 2p orbitaly. Všech pět 3d orbitalů obsahuje dvě uzlové plochy ve srovnání s jedním fo\(r\) každého p orbitalu a nulovým fo\(r\) každého s orbitalu. U tří d orbitalů jsou laloky elektronové hustoty orientovány mezi rovinami x a y, x a z a y a z; tyto orbitaly se označují jako \(3d_{xy}\), \)3d_{xz}\) a \(3d_{yz}\). Čtvrtý d orbital má laloky ležící podél os x a y; jedná se o orbital \(3d_{x^2-y^2}\). Pátý 3d orbital, nazývaný \(3d_{z^2}\), má jedinečný tvar: vypadá jako \(2p_z\) orbital kombinovaný s dalším koblihem elektronové pravděpodobnosti ležícím v rovině xy. Navzdory svému zvláštnímu tvaru je orbital \(3d_{z^2}\) matematicky ekvivalentní s jiným orbitálem \(r\) fou\(r\) a má stejnou energii. Na rozdíl od p orbitalů je fáze vlnové funkce d orbitalů stejná pro opačné páry laloků. Jak je znázorněno na obrázku \(\PageIndex{5}\), fáze vlnové funkce je kladná pro dva laloky orbitalu \(dz^2\), které leží podél osy z, zatímco fáze vlnové funkce je záporná pro koblihu elektronové hustoty v rovině xy. Stejně jako u s a p orbitalů se s rostoucím n zvětšuje velikost d orbitalů, ale celkové tvary zůstávají podobné těm, které jsou znázorněny na obrázku \(\PageIndex{5}\).
f Orbitaly (l=3)
Principální slupky s n = 4 mohou mít podslupky s l = 3 a ml hodnoty -3, -2, -1, 0, +1, +2 a +3. Tyto podpouzdra se skládají ze sedmi f orbitalů. Každý f orbital má tři uzlové plochy, takže tvaryi\(r\) jsou složité. Vzhledem k tomu, že orbitaly f nejsou zvláště důležité pro\(r\) ou\(r\) účely, nebudeme se jimi dále zabývat a orbitaly s vyššími hodnotami l nebudeme probírat vůbec.
Orbitální energie
Přestože jsme probrali tvary orbitalů, řekli jsme jen málo o srovnávacích energiíchi\(r\). Diskusi o orbitálních energiích začneme tím, že vezmeme v úvahu atomy o\(r\) ionty s jediným elektronem (například H o\(r\) He+).
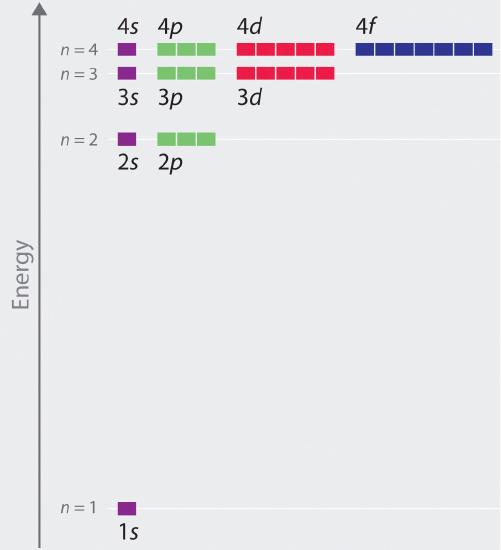
Relativní energie atomových orbitalů s n ≤ 4 pro atom vodíku jsou vyneseny na obrázku \(\PageIndex{6}\); všimněte si, že energie orbitalů závisí pouze na hlavním kvantovém čísle n. Energie orbitalů 2s a 2p vodíku jsou tedy stejné, energie orbitalů 3s, 3p a 3d jsou stejné atd. Kvantová mechanika předpovídá, že v atomu vodíku jsou všechny orbitaly se stejnou hodnotou n (např. tři orbitaly 2p) degenerované, což znamená, že mají stejnou energii. Orbitální energie získané pro vodík pomocí kvantové mechaniky jsou přesně stejné jako povolené energie vypočtené podle Boh\(r\). Na rozdíl od Bohrova modelu, který připouštěl pouze jeden orbit fo\(r\) každé energetické hladiny, však kvantová mechanika předpovídá, že v hlavním obalu n = 2 existují 4 orbitaly s různým rozložením elektronové hustoty (jeden 2s a tři 2p orbitaly), v hlavním obalu n = 3 9 a v hlavním obalu n = 4 16 orbitalů.Různé hodnoty l a ml pro jednotlivé orbitaly v dané hlavní slupce nejsou důležité pro pochopení emisních o\(r\) absorpčních spekter atomu vodíku za většiny podmínek, ale vysvětlují rozštěpení hlavních čar, které pozorujeme při umístění atomů vodíku do magnetického pole. Obrázek \(\PageIndex{6}\) ukazuje, že s rostoucí hodnotou n se energetické hladiny přibližují k sobě\(r\) a k sobě\(r\), jak se očekávalo vzhledem k závislosti orbitálních energií na 1/n2.
Energie orbitalů v jakémkoli druhu s jedním elektronem lze vypočítat pomocí mino\(r\) varianty Bohrovy rovnice, kterou lze rozšířit na jiné jednoelektronové druhy zahrnutím náboje jádra \(Z\) (počet protonů v jádře):
\
Obecně platí, že energie i poloměr klesají s rostoucím nábojem jádra\(r\). Nejstabilnější orbitaly (s nejnižší energií) jsou tedy ty, které jsou nejblíže jádru. Příklad: v základním stavu atomu vodíku je jediný elektron v orbitalu 1s, zatímco v prvním excitovaném stavu atom absorboval energii a elektron se dostal na jeden z orbitalů n = 2. U iontů s jediným elektronem závisí energie daného orbitalu pouze na n a všechny podpouzdra v rámci hlavní slupky, například orbitaly \(p_x\), \(p_y\) a \(p_z\), jsou degenerované.
Shrnutí
Chemicky důležité typy atomových orbitalů fou\(r\) odpovídají hodnotám \(\ell = 0\), \(1\), \(2\) a \(3\). Orbitaly s \(\ell = 0\) jsou s orbitaly a jsou sféricky symetrické, s největší pravděpodobností výskytu elektronu v jádře. Všechny orbitaly s hodnotami \(n > 1\) a \(ell = 0\) obsahují o\(r\) více uzlů. Orbitaly s hodnotou \(\ell = 1\) jsou p orbitaly a obsahují uzlovou rovinu, která zahrnuje jádro, čímž vzniká tvar činky. Orbitaly s \(\ell = 2\) jsou d orbitaly a mají složitější tvar s nejméně dvěma uzlovými plochami. Orbitaly s \(\ell = 3\) jsou f orbitaly, které jsou ještě složitější.
Protože průměrná vzdálenost od jádra určuje energii elektronu, má každý atomový orbital s daným souborem kvantových čísel přiřazenou určitou energii, energii orbitalu.
\
V atomech o\(r\) iontů s jediným elektronem mají všechny orbitaly se stejnou hodnotou \(n\) stejnou energii (jsou degenerované) a energie hlavních slupek plynule rostou s rostoucí hodnotou \(n\). O atomu o\(r\) iontu s elektronem(y) v orbitalu(ích) s nejnižší energií se říká, že je v základním stavu, zatímco o atomu o\(r\) iontu, v němž jeden o\(r\) více elektronů zaujímá orbitaly s vyšší energií, se říká, že je v excitovaném stavu.
Přispěvatelé a atributy
-
Změnil Joshua Halpern (Howard University)
.