Asymptota je přímka, ke které se graf blíží, ale neprotíná ji.
V této lekci se naučíme najít svislé asymptoty, vodorovné asymptoty a šikmé (šikmé) asymptoty racionálních funkcí.
Související témata:
Další lekce o Calculus

Následující obrázek ukazuje různé typy asymptot: vodorovné asymptoty, svislé asymptoty a šikmé asymptoty. Posuňte stránku dolů, kde najdete další příklady a řešení, jak najít asymptoty.

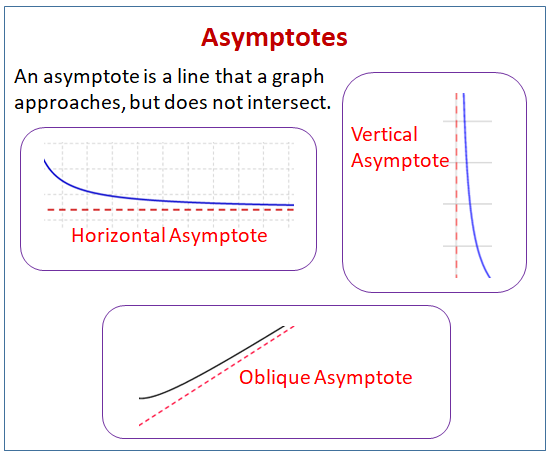
Jak určit svislou asymptotu?

Metoda 1: Použijte definici svislé asymptoty

Přímka x = a se nazývá svislá asymptota křivky y = f(x), jestliže platí alespoň jedno z následujících tvrzení.

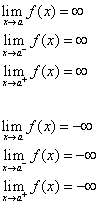
Metoda 2:

Pro racionální funkce jsou vertikální asymptoty svislé přímky, které odpovídají nulám jmenovatele.
Dáme-li racionální funkci f(x)

Krok 1: Zapíšeme f(x) v redukovaném tvaru

Krok 2: Je-li x – c činitel ve jmenovateli, pak x = c je vertikální asymptota.

Příklad:

Najděte vertikální asymptoty

Řešení:

Metoda 1: Použijte definici svislé asymptoty.

Je-li x blízké 3, ale větší než 3, pak jmenovatel x – 3 je malé kladné číslo a 2x je blízké 8.

Pokud je x větší než 3, pak jmenovatel x – 3 je malé kladné číslo. Tedy je velké kladné číslo.

Intuitivně vidíme, že

Podobně, jestliže x je blízké 3, ale menší než 3, pak x – 3 je malé záporné číslo a 2x je blízké 8. Takže je velké záporné číslo.

Přímka x = 3 je svislá asymptota.

Metoda 2:

Krok 1: f(x) je již v redukovaném tvaru.

Krok 2: Jmenovatel je x – 3, a proto je svislá asymptota v bodě x = 3.

Krok 3: Jmenovatel je x – 3, a proto je svislá asymptota v bodě x = 3.

Nalézání vertikálních asymptot racionálních funkcí

Co hledat, abychom našli vertikální asymptoty racionálních funkcí.

• Zobrazit řešení krok za krokem

Vertikální asymptoty racionálních funkcí:

• Zobrazit řešení krok za krokem

Jak najít vertikální asymptoty racionálních funkcí

• Zobrazit řešení krok za krokem

Jak určit horizontální asymptotu?

Metoda 1: Použijte definici vodorovné asymptoty

Přímka y = L se nazývá vodorovnou asymptotou křivky y = f(x), jestliže buď

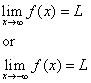
Metoda 2: Použijte definici vodorovné asymptoty:

Pro racionální funkci f(x)

Je-li stupeň x v čitateli menší než stupeň x ve jmenovateli, pak y = 0 je horizontální asymptota.

Je-li stupeň x v čitateli roven stupni x ve jmenovateli, pak y = c, kde c získáme dělením předních koeficientů.

Příklad:

Najděte vodorovnou a svislou asymptotu funkce.

Řešení:

Metoda 1:

Vydělte čitatele i jmenovatele x.

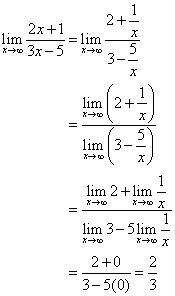
Přímka je vodorovná asymptota.

Způsob 2:

Stupeň x v čitateli je roven stupni x ve jmenovateli.

Dělíme-li vedoucí koeficienty, dostaneme

Přímka je vodorovná asymptota.

Zkratka pro hledání vodorovných asymptot racionálních funkcí

Několik triků, které velmi usnadní hledání vodorovných asymptot racionálních funkcí

• Zobrazit řešení krok za krokem

Toto video poskytne základní přehled o vodorovných asymptotách. Určíme, zda dané racionální funkce mají vodorovné asymptoty a jaké jsou.

• Show Step-by-step Solutions

V tomto videu se budeme podrobněji zabývat pravidly pro vodorovné asymptoty.

• Show Step-by-step Solutions

Oblique Asymptote or Slant Asymptote

Některé křivky mají asymptoty šikmé, tedy ani vodorovné, ani svislé.

Pokud , pak se přímka y = mx + b nazývá šikmá nebo šikmá asymptota, protože svislé vzdálenosti mezi křivkou y = f(x) a přímkou y = mx + b se blíží 0.

U racionálních funkcí se šikmé asymptoty vyskytují, když je stupeň čitatele o jedna větší než stupeň jmenovatele. V takovém případě lze rovnici šikmé asymptoty najít dlouhým dělením.

Příklad:

Najděte asymptoty funkce

Řešení:

Protože jmenovatel x2 + 1 není nikdy 0, neexistuje svislá asymptota.

Protože stupeň x v čitateli je větší než stupeň x ve jmenovateli, neexistuje vodorovná asymptota.

Protože stupeň x v čitateli je o jedna větší než stupeň x ve jmenovateli, můžeme použít dlouhé dělení k získání šikmé asymptoty.

Přímka y = x je tedy šikmou asymptotou.

Zjištění šikmých asymptot racionálních funkcí

V tomto videu je popsáno, kdy má racionální funkce šikmou asymptotu, stručně popsáno, co je to šikmá asymptota, a poté provedeny dva příklady.

• Ukázat řešení krok za krokem

Najít asymptoty racionální funkce (svislé, vodorovné a šikmé/kosmé)

Toto video ukazuje, jak najít svislé asymptoty a šikmé/kosmé asymptoty racionální funkce.

• Ukázat řešení krok za krokem

Nalezení všech asymptot racionální funkce (svislé, vodorovné a šikmé / šikmé)

Podíváme se na funkci a nalezneme svislou asymptotu a také dojdeme k závěru, že neexistují žádné vodorovné asymptoty, ale že existuje šikmá asymptota. Poté použijeme dlouhé dělení k nalezení šikmé asymptoty.

• Ukázat řešení krok za krokem

Vyzkoušejte níže uvedenou bezplatnou kalkulačku a řešitele úloh Mathway k procvičení různých matematických témat. Vyzkoušejte si uvedené příklady nebo zadejte vlastní úlohu a zkontrolujte si odpověď pomocí vysvětlení krok za krokem.