Následuje můj pohled na některé matematické problémy údajně „common core math“ nebo „new math“, které kolují po internetu. Mám pocit, že nám ukazují špatně zaměřenou implementaci CCS.
Mějte na paměti, že ne vše, co vidíte v učebnicích matematiky nebo na internetu, je správně provedeno na základě CCS. V některých příkladech, které vidíte, to vypadá, jako by lidé při řešení matematických úloh podle standardů Common Core zahodili zdravý rozum!“
Nepřekvapuje mě, že implementace skončila na některých místech „zpackaně“. CCS jsou pro většinu učitelů takovou změnou, že potřebují hodně podpory a převýchovy, než budou muset podle nich učit.
Vždycky jsem si myslel, že HLAVNÍM problémem, kterému čelí výuka matematiky na základních stupních veřejných škol, je to, že mnoho učitelů základních škol nerozumí matematice natolik, aby ji dokázali správně vyučovat i na základním stupni. Mnozí z nich například nerozumějí pojmům, důvodům a důvodům algoritmů, které učí. Není to jejich vina – problém pramení z toho, co se učili při přípravě učitelů a ve svém vlastním školství.
I samotný dokument se standardy je místy poněkud obtížně srozumitelný. Jeho čtení vyžaduje určité přemýšlení. Přál bych si, aby někdo vydal brožuru, která by standardy vysvětlovala jednoduchým jazykem a na mnoha příkladech.“
Špatné příklady „common core“ nebo „nové matematiky“
Příklad 1
Nedávno jsem na Facebooku viděl obrázek strategie odčítání, který tvrdil, že je z učebnice matematiky pro 1. třídu a že jde o „Common Core math“.“
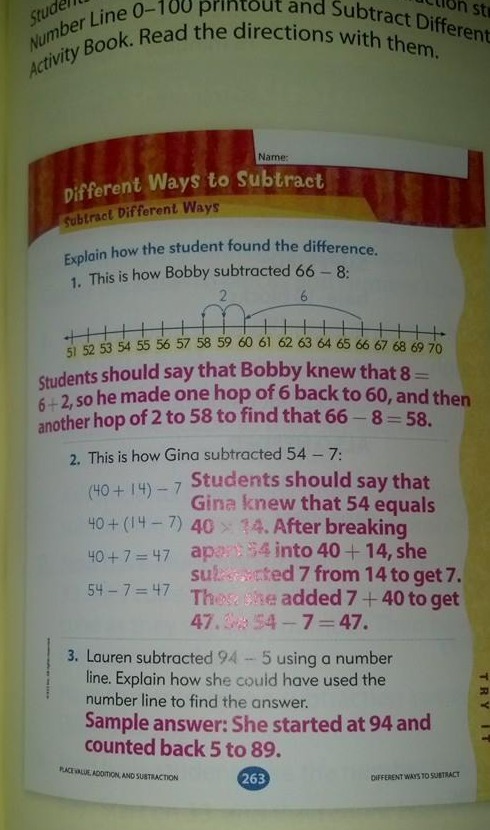
Myslím si, že metoda 2 je pro 1. třídu příliš obtížná, a dokonce i metodu 1 bych nechal pro 2. třídu.
Však se zdá, že ta kniha ani není v souladu se standardy Common Core. Standardy pro 1. třídu prostě takovéto úlohy na odčítání neobsahují!“
Takto to najdeme ve standardech:
Sčítání a odčítání do 20.
1.OA.5
Připojit počítání ke sčítání a odčítání (např. počítáním na 2 přičíst 2).
1.OA.6.
Sčítat a odčítat do 20, prokázat plynulost při sčítání a odčítání do 10. Používá strategie, jako je počítání; vytváření desítek(např. 8 + 6 = 8 + 2 + 4 = 10 + 4 = 14); rozkládání čísla vedoucího k desítce (např. 13 – 4 = 13 – 3 – 1 = 10 – 1 = 9); používání vztahu mezi sčítáním a odčítáním (např. když víme, že 8 + 4 = 12, víme, že 12 – 8= 4); a vytváření ekvivalentních, ale jednodušších nebo známých součtů (např, sčítání 6 + 7 vytvořením známého ekvivalentu 6 + 6 + 1 = 12 + 1 = 13).
Příklad v učebnici se zdá, že chce řešit výše uvedený 1.OA.6, ale ten se zjevně týká sčítání a odčítání do 20, nikoliv větších čísel.
Dále ve standardech pro 1. stupeň vidíme dva standardy, které se týkají odčítání dvouciferných čísel (do 100):
1.NBT.5.
Podle dvouciferného čísla mentálně najít o 10 větší nebo o 10 menší číslo, aniž by bylo nutné počítat; vysvětlit použité zdůvodnění.
1.NBT.6.
Odčítat násobky 10 v rozmezí 10-90 od násobků 10 v rozmezí 10-90 (kladné nebo nulové rozdíly) s použitím konkrétních modelů nebo nákresů a strategií založených na hodnotě místa, vlastnostech operací a/nebo vztahu mezi sčítáním a odčítáním; propojit strategii s písemnou metodou a vysvětlit použité zdůvodnění.
Poznámka Marie: jedná se o odčítání, jako je 34 – 20 nebo 89 – 60.
ale ani jedno z toho nezahrnuje odčítání, jako je 54 – 7 nebo 82 – 6. Ty jsou ve 2. třídě:
2.NBT.5
Plynulé sčítání a odčítání do 100 s využitím strategií založených na hodnotě místa, vlastnostech operací a/nebo vztahu mezi sčítáním a odčítáním.
Všimněte si, že standard pro 2. ročník nespecifikuje, JAK se odčítá (zda se používají mentální matematické strategie, nebo se čísla píší pod sebe a půjčují/skupují).
Příklad 2
Od společnosti Houghton Mifflin, údajně:
Juanita chce dát svým kamarádům sáčky se samolepkami. Každému kamarádovi chce dát stejný počet samolepek. Není si jistá, jestli potřebuje 4 sáčky nebo 6 sáčků samolepek. Kolik samolepek by mohla koupit, aby jí žádné samolepky nezbyly?“
Problém se samolepkami souvisí s pojmem nejmenší společný násobek (LCM). (Odpověď zní, že by měla koupit 12, 24, 36 nebo jakýkoli jiný násobek 12 samolepek, protože pak je může rozdělit buď do 4 pytlů, nebo do 6 pytlů.)
Jistě, úloha je VELMI nejasná a špatně formulovaná. Odhaduji, že brožura, ve které se to objevuje, je prostě neupravená. Není to chyba samotných norem. Souhlasím s Bartem Goddardem na matematickém fóru. Je to příznak slepého spěchu při tvorbě „reálných“ příběhových úloh, které jsou nakonec nesmyslné.
Z PDF dokumentu, ve kterém se objevuje, usuzuji, že úloha je určena pro 4. třídu, protože všechny ostatní slovní úlohy v brožuře odpovídají standardům pro 4. třídu (činitelé, prvočísla). Ale v CCS není ve standardech pro 4. třídu uveden ani nejmenší společný násobek (je v 6. třídě)!!! Něco se s tou slovní úlohou opravdu nepovedlo.
Příklad 3
Znovu údajně od Houghton Mifflin pro 1. stupeň. To odpovídá normě, kterou jsem již citoval výše:
Sčítání a odčítání do 20.
1.OA.6.
Sčítání a odčítání do 20, prokázání plynulosti při sčítání a odčítání do 10.
. Používá strategie, jako je počítání; vytváření desítek(např. 8 + 6 = 8 + 2 + 4 = 10 + 4 = 14); rozkládání čísla vedoucího k desítce (např. 13 – 4 = 13 – 3 – 1 = 10 – 1 = 9); používání vztahu mezi sčítáním a odčítáním (např. 10 – 1 = 9), když víme, že 8 + 4 = 12, víme, že 12 – 8 = 4); a vytváření ekvivalentních, ale jednodušších nebo známých součtů (např. sčítání 6 + 7 vytvořením známého ekvivalentu 6 + 6 + 1 = 12 + 1 = 13).
Nejprve je třeba říci, že strategie „vytváření desítky“ se týká PŘIDÁVÁNÍ, nikoli odčítání. Při odčítání se tomu říká „rozkládání čísla vedoucí k desítce“. V návodu by tedy mělo být napsáno: „Který ukazuje způsob rozkladu čísla vedoucího k desítce?“. Mám pocit, že je naprostý NESMYSL vyžadovat po žácích 1. stupně, aby znali takovou terminologii.
Je tu ale ještě jeden problém. Pokud si skutečně přečtete všechny standardy, všimnete si, že na několika jiných místech se po žácích požaduje, aby vysvětlili použité zdůvodnění nebo spojili určitou vizuální metodu se strategií, ale v tomto standardu NE!“
Tento standard vnímám tak, že učitelé mají UČIT různé zmíněné trategie a pak dávat žákům PROSTÉ úlohy na sčítání a odčítání v rámci 20, jako je 15 – 8 a 10 – 6.
Podle mého názoru je to tak, že učitelé mají učit různé zmíněné trategie. Nevidím v tomto standardu požadavek, aby žáci rozpoznali, zda určitý vizuální model odpovídá určité strategii.
Znovu to vypadá, že autorka odhazuje zdravý rozum… a ve skutečnosti standardům nerozumí.
Příklad 4
Následující příklad je velmi špatně formulovaný, ale KONCEPT, který za ním stojí, je velmi dobrý a najdete ho i v Matematickém mamutu. Dokážu si tedy domyslet, co chce.
Vidíte pět čtverců. Některé z nich vybarvi modře a zbytek červeně. To je jasné.
Poté stejným způsobem vybarvi čtverce v „číselné vazbě“. Vazba čísel přechází do těchto tří koleček. Dítě, které bylo přítomno hodině, kde učitel učí číselné vazby, snad ví, co to znamená. Je to stejný koncept jako rodina faktů… horní číslo je součet nebo celkový součet (5) a čísla, která jdou do spodních koleček, odpovídají tomu, kolik jsi vybarvil modře a kolik červeně, v tomto případě 1 a 4.
Takže myslím, že skrytými partnery jsou také 1 a 4.
Podívej se na to. Ukažte prsty 1 a 4 dospělému. Nakonec vybarvi 1 a 4 prsty na obrázku (a ne své vlastní prsty, jak to zní).
Podle mého názoru je část o prstech superflousní a matoucí. Nicméně koncept číselných vazeb je mnohem starší než CCS. Číselné vazby vlastně nejsou v CCS zmíněny, ačkoli se vážou k této normě:
1.OA.4
Pochopit odčítání jako úlohu s neznámým součtem. Například odečíst 10 – 8 nalezením čísla, které po přičtení k 8 tvoří 10.
a s tímto
1.OA.6.
Přičítat a odečítat do 20, prokázat plynulost sčítání a odčítání do 10.
Nevím, proč je tento pracovní list s vazbou čísel uveden jako příklad matematiky Common Core. Mnohem lépe by se hodil název příklad špatně formulovaného pracovního listu z matematiky, který MŮŽE pocházet i z doby před Common Core (a je jen znovu použit v tomto konkrétním učebním plánu)… protože, jak jsem řekl, číselné vazby v CCS zmíněny NEJSOU.
Co matematické standardy Common Core nejsou
- Nejsou „novou matematikou“. Ve srovnání s mnoha učebními osnovami matematiky používanými v roce 2000, které kladly důraz na netradiční algoritmy, jsou CCS jasným posunem k tradičním algoritmům a memorování. Podívejte se na tyto konkrétní standardy:
2.OA.2
Plynulé sčítání a odčítání do 20 s použitím mentálních strategií. Do konce 2. třídy zná zpaměti všechny součty dvou jednociferných čísel.
Poznámka Marie: jedná se o základní fakta o sčítání, jako je 7 + 7 nebo 5 + 4. Na konci 2. třídy zná zpaměti všechny součty dvou jednociferných čísel.3.OA.7
Plynulé násobení a dělení do 100 s využitím strategií, jako je vztah mezi násobením a dělením (např. když víme, že 8 × 5 = 40, víme, že 40 ÷ 5 = 8) nebo vlastnosti operací. Na konci 3. třídy zná zpaměti všechny součin dvou jednociferných čísel.
Poznámka Marie: to znamená tabulky násobení a základní fakta o dělení.4.NBT.4
Plynulé sčítání a odčítání víceciferných celých čísel s použitím standardního algoritmu.5.NBT.5
Plynulé násobení víceciferných celých čísel s použitím standardního algoritmu.
Poznámka Marie: neznamená to, že žáci násobí víceciferná celá čísla pouze v 5. ročníku; to se učí i ve 3. a 4. ročníku. - Standardy nevnucují učitelům a žákům podivné strategie nebo vizuální modely. Mnohé standardy to nechávají na učitelích a žácích. Například:
2.NBT.5
Plynulé sčítání a odčítání do 100 s použitím strategií založených na hodnotě místa, vlastnostech operací a/nebo vztahu mezi sčítáním a odčítáním.Všimněte si „a/nebo“ ve výše uvedené větě. To znamená, že učitelé a žáci NEJSOU omezeni na používání konkrétních strategií, ani jim není řečeno, aby používali několik strategií. Tradiční algoritmus „půjčování“ je strategie založená na hodnotě místa, takže je zahrnuta právě zde v 2.NBT.5.
2.NBT.9
Vysvětlete, proč fungují strategie sčítání a odčítání s využitím hodnoty místa a vlastností operací. Vysvětlení lze podpořit nákresy nebo předměty.Říká „lze podpořit nákresy“, ale nenutí vás k tomu, ani vás neomezuje na použití konkrétního vizuálního modelu nebo typu nákresu.
3.OA.3
Používat násobení a dělení do 100 k řešení slovních úloh insituací zahrnujících stejné skupiny, pole a měrné veličiny,např. pomocí nákresů a rovnic se symbolem neznámého čísla k znázornění problému.Žák nemusí používat nákres. To je pouze uvedeno jako možnost.
4.NBT.5
Násobit celé až čtyřciferné číslo jednociferným celým číslem a násobit dvě dvouciferná čísla s využitím strategií založených na hodnotě místa a vlastnostech operací. Ilustrovat a vysvětlit výpočet pomocí rovnic, pravoúhlých tabulek a/nebo areamodelů.Všimněte si slova „a/nebo“. Ilustrujte výpočet, ale stačí jej znázornit pomocí rovnic. Nemusíte jej ilustrovat pomocí polí.
Také některé standardy zmiňují konkrétní vizuální model, například číselnou přímku nebo model pravoúhlé plochy, ale to je méně časté než dát na výběr jako ve výše uvedených standardech.
Konceptuální matematika
Existují některé standardy, které zasahují do konceptuální stránky matematiky a kterým učitelé základních škol nemusí rozumět, pokud nejsou poučeni o tom, co znamenají; například:
5. Vymezení pojmů v matematice. NF.7b
Vyložit dělení celého čísla jednotkovým zlomkem a vypočítat takové kvocienty. Například vytvořit dějový kontext pro 4 ÷ (1/5) a použít vizuální model zlomku k zobrazení kvocientu. Použijte vztah mezi násobením a dělením a vysvětlete, že 4 ÷ (1/5) = 20, protože 20 × (1/5) = 4.
Jedním z takových příběhových problémů může být: Kolik kousků dlouhých 1/5 stopy můžete vystřihnout z kusu materiálu o délce 4 stopy? Vizuální model by mohl znázorňovat 4 celky rozdělené na pětiny. Pak můžeme spočítat, že 4 celky mají celkem 20 pětin.
5.NF.4b
Najděte plochu obdélníku se zlomkovými délkami stran tak, že jej obložíte jednotkovými čtverci s příslušnými jednotkovými zlomkovými délkami stran, a ukažte, že plocha je stejná, jakou bychom zjistili vynásobením délek stran. Vynásobte zlomkové délky stran, abyste zjistili plochyobdélníků, a znázorněte součin zlomků jako plochy obdélníků.
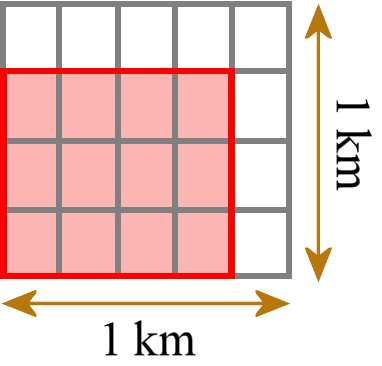To znamená například obdélník s délkami stran 3/4 km a 4/5 km. Pak jej obložíme malými jednotkovými obdélníky (nikoliv jednotkovými čtverci; zde má sama norma nesprávnou terminologii), které mají každý délku strany 1/4 km a 1/5 km.
Můžeme spočítat, kolik malých dlaždic potřebujeme. Potřebujeme 12 takových destiček. Každá dlaždice má plochu 1/20 km2, takže celková plocha je 12/20 km2. Pak zkontrolujeme a porovnáme, že dostaneme stejnou odpověď, jako kdybychom délky obou stran vynásobili běžným násobením zlomků (3/4 km × 4/5 km = 12/20 km2).
Takové úlohy jsem měl v učebnicích vždycky – i předtím, než se objevil CCS.
Někteří lidé tvrdí, že děti takové pojmové chápání nepotřebují nebo že je to příliš obtížné. Osobně s tím nesouhlasím. Vždy jsem se snažil (i před CCS) vysvětlovat pojmy aritmetiky zlomků tak, aby žáci neskončili „slepě podle pravidel“ a dokázali počítat se zlomky, jen když si náhodou pravidlo správně zapamatují. Vždy jsem kladl důraz na pojmové chápání v matematice (jak moji čtenáři vědí!).
Doufám však, že chápete, že některé z těchto věcí mohou být pro učitele a rodiče ve škole neznámé, a proto není divu, že je pro ně dodržování standardů Common Core obtížné.
Doufám, že řada Math Mammoth Light Blue a jednotky, které prodávám ve svých obchodech Teachers Pay Teachers a Teachers‘ Notebook, mohou pomoci těm učitelům &rodičům, kteří potřebují materiály sladěné s Common Core. A jak jsem řekl, i vy ostatní je můžete s důvěrou používat. Neobsahují žádnou „podivnou“ nebo nesmyslnou matematiku, ale jako vždy jsou jednoduše založeny na pevném základu výuky matematických pojmů spolu s postupy.
Maria Miller
.