Podobně jako u P-regulátoru i u proporcionálně-integrálního (PI) algoritmu dochází k výpočtu a přenosu výstupního signálu regulátoru (CO) v každém vzorkovacím čase T na koncový regulační prvek (např. ventil, čerpadlo s proměnnými otáčkami). Vypočtený CO z PI algoritmu je ovlivněn parametry ladění regulátoru a chybou regulátoru, e(t).
PI regulátory mají dva parametry ladění, které se nastavují. To je sice činí náročnějšími na ladění než regulátor pouze P, ale nejsou tak složité jako tříparametrový regulátor PID.
Integrální působení umožňuje regulátorům PI eliminovat offset, což je hlavní slabina regulátoru pouze P.
. PI regulátory tak poskytují rovnováhu mezi složitostí a schopnostmi, díky níž jsou zdaleka nejpoužívanějším algoritmem v aplikacích řízení procesů.
Algoritmus PI
Různí dodavatelé odlévají v podstatě stejný algoritmus do různých forem, zde však prozkoumáme to, co je různě popisováno jako závislá, ideální, spojitá, polohová forma:
![]()
Kde:
CO = výstupní signál regulátoru (výstupní vodič)
CObias = zkreslení regulátoru nebo nulová hodnota; nastavená beznárazovým přenosem, jak je vysvětleno níže
e(t) = aktuální chyba regulátoru, definovaná jako SP – PV
SP = žádaná hodnota
PV = měřená procesní veličina (vodič dovnitř)
Kc = zesílení regulátoru, parametr ladění
Ti = doba vynulování, parametr ladění
První dva členy napravo od znaménka rovnosti jsou totožné s regulátorem P-Only, na který je odkaz v horní části tohoto článku.
Integrální režim regulátoru je posledním členem rovnice. Jeho funkcí je integrovat nebo průběžně sčítat chybu regulátoru, e(t), v čase.
Několik věcí bychom měli vědět o parametru časového ladění nulování, Ti:
| ▪ | Dává samostatnou váhu integrálnímu členu, takže vliv integrální akce lze nezávisle nastavit. |
| ▪ | Je ve jmenovateli, takže menší hodnoty poskytují větší váhu (tj. zvyšují vliv) integrálního členu. |
| ▪ | Má jednotky času, takže je vždy kladný. |
Funkce proporcionálního členu
Stejně jako u regulátoru P-Only, proporcionální člen PI regulátoru, Kc-e(t), přičítá nebo odečítá od CObias na základě velikosti chyby regulátoru e(t) v každém čase t.
Jakmile e(t) roste nebo se zmenšuje, částka přičítaná k CObias roste nebo se zmenšuje okamžitě a úměrně. Minulá historie a aktuální trajektorie chyby regulátoru nemají na výpočet proporcionálního členu žádný vliv.
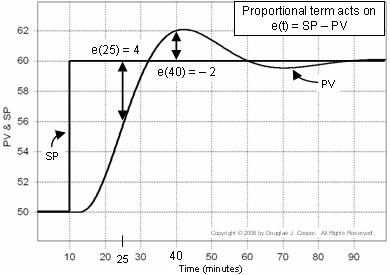
Následující graf (klikněte pro větší zobrazení) ilustruje tuto myšlenku pro odezvu žádané hodnoty. Chyba použitá při výpočtu proporcionálního členu je znázorněna na grafu:
▪ V čase t = 25 min, e(25) = 60-56 = 4
▪ V čase t = 40 min, e(40) = 60-62 = -2
Připomeneme-li, že chyba regulátoru e(t) = SP – PV, můžeme místo toho, abychom na PV a SP pohlíželi jako na samostatné trajektorie, jak jsme učinili výše, vypočítat a vykreslit e(t) v každém bodě času t.
Níže (klikněte pro větší zobrazení) jsou identická data jako výše, pouze jsou přepracována jako graf samotného e(t). Všimněte si, že v grafu výše je PV = SP = 50 pro prvních 10 minut, zatímco v grafu chyby níže je e(t) = 0 pro stejný časový úsek.
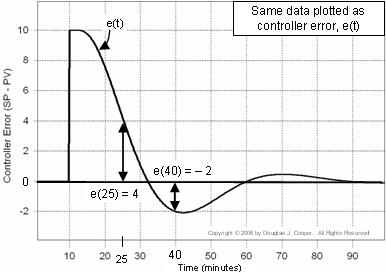
Tento graf je užitečný, protože nám pomáhá vizualizovat, jak chyba regulátoru průběžně mění velikost a znaménko v průběhu času.
Funkce integrálního členu
Zatímco proporcionální člen uvažuje aktuální velikost e(t) pouze v okamžiku výpočtu regulátoru, integrální člen uvažuje historii chyby, neboli jak dlouho a jak daleko byla měřená procesní veličina od žádané hodnoty v průběhu času.
Integrace je neustálé sčítání. Integrace chyby v čase znamená, že sečteme celou historii chyby regulátoru až do současnosti, počínaje okamžikem, kdy byl regulátor poprvé přepnut na automatiku.
Chybou regulátoru je e(t) = SP – PV. V níže uvedeném grafu (klikněte pro větší zobrazení) je integrální součet chyby vypočten jako stínované oblasti mezi stopami SP a PV.
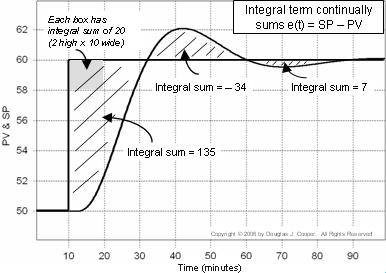
Každé políčko v grafu má integrální součet 20 (2 na výšku krát 10 na šířku). Spočítáme-li počet políček (včetně zlomků políček) obsažených ve stínovaných oblastech, můžeme vypočítat integrální součet chyby.
Takže když PV poprvé překročí nastavený bod přibližně v čase t = 32, integrální součet vzrostl na přibližně 135. To znamená, že v okamžiku, kdy PV poprvé překročí nastavený bod v čase t = 32, integrální součet vzrostl na přibližně 135. Integrální člen PI regulátoru zapíšeme jako:
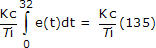
Protože je to chyba regulátoru, která řídí výpočet, získáme přímý pohled na situaci z grafu chyby regulátoru, jak je uvedeno níže (klikněte pro větší zobrazení):

Všimněte si, že integrál každé zastíněné části má stejné znaménko jako chyba. Protože se integrální součet začíná kumulovat při prvním uvedení regulátoru do automatického režimu, celkový integrální součet roste, dokud je e(t) kladné, a zmenšuje se, když je záporné.
V čase t = 60 min na grafech je integrální součet 135 – 34 = 101. V čase t = 90 min se odezva do značné míry ustálí a integrální součet je pak 135 – 34 + 7 = 108.
Integrální působení eliminuje posun
Předchozí věta obsahuje jemný, ale velmi důležitý postřeh. Odezva je v čase t = 90 min z velké části dokončena, přesto integrální součet všech chyb není nulový.
V tomto příkladu má integrální součet konečnou nebo zbytkovou hodnotu 108. V tomto případě je integrální součet nulový. Právě tato zbytková hodnota umožňuje integrálnímu působení PI regulátoru eliminovat posun.
Jak bylo uvedeno v předchozím článku, u většiny procesů řízených pouze pomocí P dochází během běžného provozu k posunu. Offset je trvalá hodnota chyby regulátoru (tj. PV se v ustáleném stavu nerovná SP).
Z regulátoru P-Only poznáme:
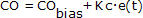
že CO se bude vždy rovnat CObias, pokud k němu něco nepřičteme nebo neodečteme.
Ve výše uvedené rovnici P-Only máme co přičíst nebo odečíst od CObias pouze tehdy, pokud e(t) není nulové. Není-li e(t) ustálené na nule, pak se PV nerovná SP a máme offset.
U PI regulátoru však:
![]()
nyní víme, že integrální součet chyb může mít po dokončení odezvy konečnou nebo zbytkovou hodnotu. To je důležité, protože to znamená, že e(t) může být nulové, a přesto můžeme mít co přičítat nebo odečítat od CObias, abychom vytvořili konečný výstup regulátoru, CO.
Takže dokud existuje nějaká chyba (dokud e(t) není nulové), integrální člen bude růst nebo se zmenšovat, aby ovlivnil CO. Změny CO ustanou teprve tehdy, když se PV po delší dobu rovná SP (když e(t) = 0).
V tomto okamžiku může mít integrální člen zbytkovou hodnotu, jak bylo právě řečeno. Tato zbytková hodnota z integrace po přičtení k CObias v podstatě vytvoří novou celkovou hodnotu zkreslení, která odpovídá nové provozní úrovni.
V důsledku toho integrální působení neustále obnovuje hodnotu zkreslení, aby se eliminoval posun při změně provozní úrovně.
Úskalí PI regulace
Při použití PI algoritmu se objevují problémy:
| ▪ | Dva ladicí parametry se vzájemně ovlivňují a jejich vliv musí konstruktér vyvážit. |
| ▪ | Integrální člen má tendenci zvyšovat oscilační nebo valivé chování odezvy procesu. |
Protože se oba parametry ladění vzájemně ovlivňují, může být náročné dospět k „nejlepším“ hodnotám ladění. Hodnota a důležitost našeho návrhu a předpisu laděnívzrůstá s tím, jak se regulátor stává složitějším.
Inicializace regulátoru pro beznárazový přenos
Když přepínáme jakýkoli regulátor z ručního režimu na automatický (z otevřené smyčky na uzavřenou), chceme, aby výsledek byl bezproblémový. To znamená, že nechceme, aby přepnutí způsobilo náhlé řídicí akce, které by ovlivnily nebo narušily náš proces
Takového požadovaného výsledku při přepnutí dosáhneme tím, že inicializujeme integrální součet chyb regulátoru na nulu. Rovněž žádanou hodnotu a hodnotu zkreslení regulátoru inicializujeme nastavením:
▪ SP rovná se aktuální PV
▪ CObias rovná se aktuální CO
Při nastavení integrální sumy chyby na nulu není k CObias co přičítat ani odčítat, což by způsobilo náhlou změnu aktuálního výstupu regulátoru. S žádanou hodnotou rovnou měřené procesní veličině neexistuje žádná chyba, která by řídila změnu našeho CO. A s předpětím regulátoru nastaveným na naši aktuální hodnotu CO jsme standardně připraveni udržovat aktuální provoz.
Při přechodu z ručního režimu na automatický tak máme „převod bez nárazů“ bez překvapení. To je výsledek, který každý ocení.
Čas resetování versus rychlost resetování
Různí výrobci odlévají své řídicí algoritmy do mírně odlišných podob. Někteří používají spíše proporcionální pásmo než zesílení regulátoru. Někteří také používají rychlost vynulování, Tr, místo času vynulování. Ty jsou jednoduše navzájem inverzní:
Tr = 1/Ti
Nezáleží na tom, jak jsou vyjádřeny parametry ladění, všechny PI algoritmy jsou stejně schopné.
Než však začnete ladit svůj regulátor, je velmi důležité znát jeho výrobce, protože hodnoty parametrů musí odpovídat konkrétní podobě algoritmu.Komerční software pro návrh a ladění regulátorů tento problém automaticky vyřeší za vás.
Implementace PI regulátoru
V tomto článku se zabýváme návrhem, laděním a implementací PI regulátoru na výměníku tepla a v tomto článku na gravitačně vypouštěných nádržích.
.