Eulerova identita se zdá být nepochopitelná:

Vychází z obecnějšího vzorce:

Yowza — vztahujeme imaginární exponent k sinusu a kosinusu! A když nějak dosadíme pí, dostaneme -1? Mohlo by to být vůbec intuitivní?“

Ne podle matematika 19. století Benjamina Peirce:

Je to naprosto paradoxní; nemůžeme to pochopit a nevíme, co to znamená, ale dokázali jsme to, a proto víme, že to musí být pravda.

Argh, z tohoto přístupu se mi vaří krev! Vzorce nejsou magická zaklínadla, která se mají naučit nazpaměť: musíme, musíme, musíme najít vhled. Tady je ten můj:

Eulerův vzorec popisuje dva rovnocenné způsoby pohybu po kružnici.

To je vše? Tato ohromující rovnice je o otáčení se dokola? Ano – a můžeme ji pochopit, když se opřeme o několik analogií:

• Začneme-li u čísla 1, vnímejme násobení jako transformaci, která mění číslo: $1 \cdot e^{i \pi}$
• Pravidelný exponenciální růst neustále zvyšuje 1 o určitou rychlost po určitou dobu; imaginární exponenciální růst neustále otáčí 1 za nějaký časový úsek
• Růst za „pi“ jednotek času znamená obejít pi radiánů kolem kruhu
• Takže $e^{i \pi}$ znamená začít na 1 a otočit se o pi (o polovinu kruhu), abychom se dostali na -1

To je pohled na vysoké úrovni, pojďme se ponořit do detailů. Mimochodem, pokud se vás někdo pokusí ohromit tvrzením $e^{i \pi} = -1$, zeptejte se ho na i na i-tou mocninu. Pokud to nedokážou domyslet, je pro ně Eulerův vzorec stále kouzelným zaklínadlem.

Aktualizace: Při psaní mě napadlo, že video by mohlo pomoci vysvětlit myšlenky srozumitelněji:

Pochopení cos(x) + i * sin(x)

Znak rovnosti je přetížený. Někdy tím myslíme „dosadit jednu věc za druhou“ (jako x = 3) a jindy tím myslíme „tyto dvě věci popisují stejný pojem“ (jako $\sqrt{-1} = i$).

Eulerův vzorec je ten druhý: uvádí dva vzorce, které vysvětlují, jak se pohybovat po kružnici. Pokud budeme zkoumat pohyb po kružnici pomocí trigonometrie a urazíme x radiánů:

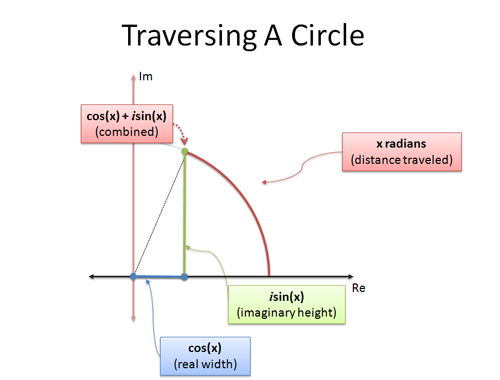
• cos(x) je souřadnice x (vodorovná vzdálenost)
• sin(x) je souřadnice y (svislá vzdálenost)

Výrok

je chytrý způsob, jak souřadnice x a y směstnat do jednoho čísla. Analogie „komplexní čísla jsou dvojrozměrná“ nám pomáhá interpretovat jediné komplexní číslo jako polohu na kružnici.

Když nastavíme x na $\pi$, pohybujeme se $\pi$ jednotek po vnější straně jednotkové kružnice. Protože celkový obvod je $2\pi$, obyčejné staré $\pi$ je v polovině cesty, což nás staví do polohy -1.

Neato: Pravá strana Eulerova vzorce ($\cos(x) + i \sin(x)$) popisuje kruhový pohyb s imaginárními čísly. Nyní zjistíme, jak toho dosahuje strana e rovnice.

Co je to imaginární růst?

Spojení souřadnic x a y do komplexního čísla je složité, ale zvládnutelné. Co však znamená imaginární exponent?“

Udělejme krok zpět. Když vidím $3^4$, představím si to takto:

• 3 je konečný výsledek okamžitého růstu (pomocí e) rychlostí ln(3). Jinými slovy: $3 = e^{\ln(3)}$
• $3^4$ je totéž jako růst do 3, ale pak roste 4x tak dlouho. Takže $3^4 = e^{\ln(3) \cdot 4} = 81$

Místo toho, abyste čísla viděli sama o sobě, můžete si je představit jako něco, k čemu e muselo „dorůst“. Reálná čísla, jako je 3, dávají úrokovou míru ln(3) = 1,1, a to je to, co e „sbírá“, když neustále roste.

Regulérní růst je jednoduchý: stále „tlačí“ číslo stejným, reálným směrem, kterým šlo. 3 × 3 ho tlačí původním směrem, takže se třikrát zvětší (9).

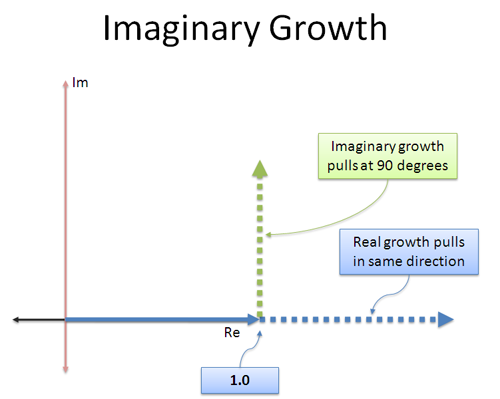
Imaginární růst je jiný: „úroky“, které získáváme, jdou jiným směrem! Je to jako tryskový motor, který byl připoután bokem – místo abychom jeli dopředu, začneme tlačit pod úhlem 90 stupňů.

Na stálém kolmém (ortogonálním) tlačení je elegantní to, že vás nezrychluje ani nezpomaluje – otáčí vás! Vezmeme-li libovolné číslo a vynásobíme-li ho i, nezměníme jeho velikost, pouze směr, kterým ukazuje.

Intuitivně vidím spojitou pomyslnou rychlost růstu takto: „Když rostu, netlačte mě dopředu ani dozadu ve směru, kterým už jdu. Místo toho mě otáčej.“

Ale neměli bychom se točit stále rychleji a rychleji?“

To mě také napadlo. Pravidelný růst se skládá v našem původním směru, takže jedeme 1, 2, 4, 8, 16, pokaždé násobíme 2x a zůstáváme v reálných číslech. Můžeme to považovat za $e^{\ln(2)x}$, což znamená růst okamžitě rychlostí ln(2) po dobu „x“ sekund.

A hele – kdyby byl náš růst dvakrát rychlejší, 2ln(2) vs ln(2), vypadalo by to stejně jako růst po dvakrát delší dobu (2x vs x). Kouzlo e nám umožňuje zaměnit rychlost a čas; 2 sekundy při ln(2) je stejný růst jako 1 sekunda při 2ln(2).

Teď si představme, že máme nějakou čistě imaginární rychlost růstu (Ri), která nás otáčí, dokud nedosáhneme i, neboli 90 stupňů vzhůru. Co se stane, když tuto rychlost zdvojnásobíme na 2Ri, budeme se otáčet mimo kružnici?“

Ne! Mít rychlost 2Ri znamená, že se prostě točíme dvakrát rychleji, případně se točíme rychlostí R dvakrát déle, ale zůstáváme na kružnici. Otáčet se dvakrát tak dlouho znamená, že jsme nyní otočeni o 180 stupňů.

Jakmile si uvědomíme, že nějaká exponenciální rychlost růstu nás může dostat z 1 na i, zvýšení této rychlosti nás jen více roztočí. Z kruhu nikdy neunikneme.

Jestliže je však naše rychlost růstu komplexní (a+bi vs Ri), pak nás reálná část (a) bude růst jako normálně, zatímco imaginární část (bi) nás bude otáčet. Nebudeme si však vymýšlet: Eulerův vzorec, $e^{ix}$, se týká čistě imaginárního růstu, který nás udržuje na kružnici (více později).

Krátká kontrola příčetnosti

Při psaní jsem si musel ujasnit několik otázek:

Proč používat $e^x$, neotáčíme snad číslem 1?

e představuje proces, který začíná na hodnotě 1 a roste nepřetržitě se 100% úrokem po dobu 1 časové jednotky.

Když píšeme e, zachycujeme celý tento proces v jediném čísle – e představuje celou tu fintu nepřetržitého růstu. Takže ve skutečnosti $e^x$ říká „začínáme od 1 a rosteme nepřetržitě o 100 % po dobu x sekund“ a začínáme od 1, jak chceme.

Ale co dělá i jako exponent?

Pro běžný exponent jako $3^4$ se ptáme:

• Jaká je implicitní míra růstu? Rosteme z 1 na 3 (základ exponentu).
• Jak tuto rychlost růstu změníme? Škálujeme ji 4x (mocninou exponentu).

Můžeme náš růst převést do formátu „e“: naše okamžitá míra je ln(3) a my ji zvýšíme na ln(3) * 4. Opět platí, že mocnina exponentu (4) právě škáluje naši míru růstu.

Když je horní exponent i (jako v $3^i$), prostě vynásobíme naši implicitní míru růstu i. Takže místo toho, abychom rostli obyčejnou starou rychlostí ln(3), rosteme rychlostí ln(3) * i.

Vrchní část exponentu modifikuje implicitní rychlost růstu spodní části.

Podrobnosti

Podívejme se na to blíže. Zapamatujte si tuto definici e:

Ten $\frac{100\%}{n}$ představuje část úroku, kterou jsme získali v každém mikroskopickém období. Předpokládali jsme, že úroková míra je 100 % v reálném rozměru – ale co kdyby byla 100 % v imaginárním směru?“

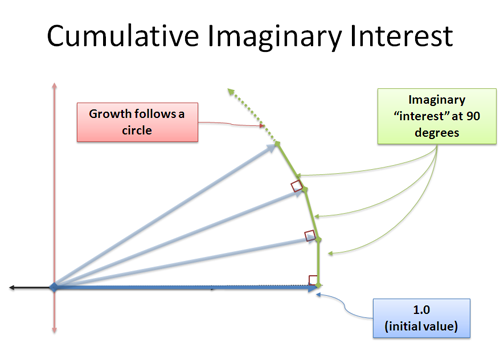
Nyní nám nově vzniklý úrok přibude ve směru 90 stupňů. Překvapivě se tím nemění naše délka – to je ošemetný pojem, protože se zdá, že vzniká trojúhelník, kde přepona musí být větší. Máme co do činění s hranicí a vzdálenost navíc je v rámci námi zadané chyby. Tomu se chci věnovat jindy, ale vezměte mě za slovo: průběžný kolmý růst vás bude otáčet. To je jádro sinusovky a kosinusovky, kde je vaše změna kolmá na vaši současnou polohu a vy se pohybujete po kružnici.

Použijeme i jednotek růstu v nekonečně malých přírůstcích, přičemž každý nás posune o 90 stupňů. Neexistuje žádné „rychlejší a rychlejší“ otáčení – místo toho se plazíme po obvodu o vzdálenost |i| = 1 (velikost i).

A hele – vzdálenost, kterou se plazíme po kružnici, je úhel v radiánech! Našli jsme další způsob, jak popsat kruhový pohyb!

Pro získání kruhového pohybu:

Takže Eulerův vzorec říká „exponenciální, imaginární růst vytyčuje kružnici“. A tato dráha je stejná jako pohyb po kružnici pomocí sinusu a kosinusu v imaginární rovině.

V tomto případě je slovo „exponenciální“ matoucí, protože po kružnici se pohybujeme konstantní rychlostí. Ve většině diskusí se předpokládá, že exponenciální růst má kumulativní, složený účinek.

Několik příkladů

Vy mi snad opravdu nevěříte? Tady je několik příkladů a jak o nich intuitivně přemýšlet.

Příklad: $e^i$

Kde je to x? Aha, je to právě 1. Intuitivně, aniž bychom museli vytahovat kalkulačku, víme, že to znamená „urazit 1 radián po jednotkové kružnici“. V hlavě vidím, jak se „e“ snaží růst o 1 na 100 % stále stejným směrem, ale i stále pohybuje kuličkou a nutí „1“ růst po okraji kružnice:

Není to nejhezčí číslo, ale je to tak. Nezapomeňte při jeho vyťukávání přepnout kalkulačku do režimu radiánů.

Příklad: $3^i$

To je ošemetné – není to v našem standardním formátu. Ale pamatujte si:

Chceme, aby na konci periody byl počáteční růst 3x, neboli okamžitá rychlost ln(3). Ale přijde i a změní tuto rychlost ln(3) na „i * ln(3)“:

Mysleli jsme si, že budeme transformovat běžnou rychlostí ln(3), o něco rychlejší než 100% nepřetržitý růst, protože e je asi 2,718. Vždycky jsme si mysleli, že budeme transformovat běžnou rychlostí ln(3). Ale kdepak, otočil jsem nás: teď se transformujeme imaginární rychlostí, což znamená, že se jen otáčíme. Kdyby i bylo regulární číslo, například 4, rostli bychom díky tomu 4x rychleji. Nyní rosteme rychlostí ln(3), ale do strany.

Měli bychom očekávat komplexní číslo na jednotkové kružnici – v rychlosti růstu není nic, co by zvětšovalo naši velikost. Řešení rovnice:

Takže místo toho, abychom skončili o „1“ jednotku kolem kružnice (jako $e^i$), skončíme o ln(3) jednotek kolem.

Příklad: $i^i$

Před pár měsíci by mě to rozplakalo. Dnes už ne! Rozebereme si transformace:

Začínáme s hodnotou 1 a chceme ji změnit. Stejně jako při řešení $3^i$, jakou okamžitou míru růstu představuje i jako základ?“

Hrm. Normálně bychom udělali ln(x), abychom získali rychlost růstu potřebnou k dosažení x na konci 1 časové jednotky. Ale pro imaginární míru? Musíme to přehnat nudlí.

Abychom začali s 1 a rostli na i, musíme začít otáčet na začátku. Jak rychle? No, potřebujeme získat 90 stupňů (pí/2 radiánů) za 1 časovou jednotku. Takže naše rychlost je $i \frac{\pi}{2}$. Nezapomeňte, že naše rychlost musí být imaginární, protože se otáčíme, nikoliv rosteme! Obyčejná stará rychlost $\frac{\pi}{2}$ je asi 1,57 a vede k pravidelnému růstu.

To by mělo dávat smysl: abychom na konci 1 jednotky otočili 1,0 na i, měli bychom za tuto dobu otočit $\frac{\pi}{2}$ o radiány (90 stupňů). Abychom tedy získali „i“, můžeme použít $e^{i \frac{\pi}{2}}$.

Uf. To popisuje i jako základ. A co exponent?

No, to druhé i nám říká, že máme změnit sazbu – ano, tu sazbu, kterou jsme tak dlouho vymýšleli! Takže místo toho, abychom se otáčeli rychlostí $i \frac{\pi}{2}$, což znamená základ i, transformujeme rychlost na:

Ty i se ruší a rychlost růstu je opět reálná! Otočili jsme naši sazbu a posunuli se do záporných čísel. A záporná míra růstu znamená, že se zmenšujeme – měli bychom očekávat, že se $i^i$ zmenší. A to se také stane:

Tada! (Vyhledejte „i^i“ na Googlu a použijte jeho kalkulačku)

Nechte si vydechnout: Můžete intuitivně zjistit, jak by se měly chovat imaginární báze a imaginární exponenty. Páni.

A jako bonus jste přišli na ln(i) — aby se $e^x$ stalo i, otočte e o $\frac{\pi}{2}$ radiánů.

Příklad: (i^i)^i

Dvojnásobný imaginární exponent? Pokud na tom trváte. Nejdříve víme, jaká bude naše rychlost růstu uvnitř závorky:

Dostaneme zápornou (zmenšující se) rychlost růstu -pi/2. To znamená, že v závorce bude záporná rychlost růstu. A nyní tuto rychlost opět upravíme o i:

A nyní máme zápornou rotaci! Obíháme kružnici rychlostí $-\frac{\pi}{2}$ za jednotku času. Jak dlouho pojedeme? No, na samém vrcholu tohoto řetězce exponentů je implicitní jednotka času „1“; implicitní výchozí hodnota je jít na 1 jednotku času (stejně jako $e = e^1$). Jedna časová jednotka nám dává rotaci $-\frac{\pi}{2}$ radiánů (-90 stupňů) neboli -i!

A jen tak pro zajímavost, kdybychom tento šílený výsledek vynásobili čtvercem:

Je to „jen“ dvojnásobná rotace: 2 je regulární číslo, takže zdvojnásobuje naši rychlost rotace na plných -180 stupňů za jednotku času. Nebo se na to můžete dívat tak, že dvakrát za sebou použijete rotaci -90 stupňů.

Na první pohled jsou to opravdu zvláštní exponenty. Ale s našimi analogiemi je můžeme brát s nadhledem.

Komplexní růst

Můžeme mít reálný i imaginární růst zároveň: reálná část nás škáluje a imaginární část nás otáčí:

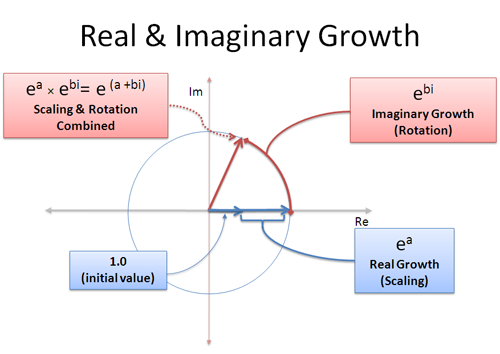
Komplexní růst jako (a + bi) je směs reálného a imaginárního růstu. Reálná část a, znamená „růst na 100 % po dobu a sekund“ a imaginární část b znamená „otáčet se po dobu b sekund“. Nezapomeňte, že rotace nemají výhodu složeného růstu, protože stále „tlačíte“ jiným směrem – rotace se sčítá lineárně.

S tímto vědomím můžeme pomocí (a+bi) znázornit libovolný bod na libovolně velké kružnici! Poloměr je $e^a$ a úhel je určen hodnotou $e^{bi}$. Je to jako vložit číslo do expandéru na dva cykly: jednou, aby narostlo do správné velikosti (a sekund), podruhé, aby se otočilo do správného úhlu (b sekund). Nebo byste ho mohli nejprve otočit a pak teprve zvětšit!“

Řekněme, že chceme znát velikost růstu, abychom se dostali na hodnotu 6 + 8i. To se vlastně ptáme na přirozený logaritmus imaginárního čísla: Jak rosteme e, abychom dostali (6 + 8i)?“

• Průměr: Jak velkou kružnici potřebujeme? No, velikost je $\sqrt{6^2 + 8^2} = \sqrt{100} = 10$. To znamená, že k dosažení této částky potřebujeme růst po dobu ln(10) = 2,3 sekundy.
• Částka k otočení: Jaký je úhel tohoto bodu? Můžeme to zjistit pomocí arctanu: atan(8/6) = 53 stupňů = 0,93 radiánu.
• Zkombinujte výsledek: ln(6+8i) = 2,3 + 0,93i

To znamená, že můžeme dosáhnout náhodného bodu (6 + 8i), pokud použijeme $e^{2.3 + .93i}$.

Proč je to užitečné?

Eulerův vzorec nám dává další způsob, jak popsat pohyb po kružnici. Ale to už jsme mohli udělat pomocí sinusu a kosinusu – co je na tom tak zvláštního?

Jde o perspektivu. Sinus a kosinus popisují pohyb z hlediska sítě, vynášejí vodorovné a svislé souřadnice.

Eulerův vzorec používá polární souřadnice — jaký je váš úhel a vzdálenost? Opět jde o dva způsoby popisu pohybu:

• Mřížková soustava:
• Polární souřadnice: Jdi 3 jednotky na východ a 4 jednotky na sever: V závislosti na problému jsou užitečnější polární nebo pravoúhlé souřadnice. Eulerův vzorec nám umožňuje převádět mezi nimi a použít nejlepší nástroj pro danou úlohu. Také proto, že $e^{ix}$ lze převést na sinus a kosinus, můžeme přepsat vzorce v trigonometrii jako variace na e, což se velmi hodí (nemusíte se učit nazpaměť sin(a+b), můžete si ho odvodit — více jindy). A je krásné, že každé číslo, ať už reálné nebo komplexní, je variací na e.

  Ale užitečnost, šmudla: nejdůležitějším výsledkem je zjištění, že matoucí rovnice se mohou stát intuitivními díky správným analogiím. Nenechte krásné rovnice, jako je Eulerova formule, zůstat kouzelným zaklínadlem – stavte na analogiích, které znáte, abyste viděli poznatky uvnitř rovnice.

  Šťastnou matematiku.

  Příloha

  Screening byl zábavný a zpětná vazba je rozhodně vítána. Myslím, že to pomáhá myšlenkám vyniknout, a procházení článku mi pomohlo najít mezery v mé intuici.

  • Brian Slesinsky má přehlednou prezentaci o Eulerově vzorci
  • Vizuální komplexní analýza má skvělou diskusi o Eulerově vzorci — viz str. 10 v náhledu knihy Google
  • Dělal jsem přednášku o matematice a analogiích, která vysvětluje Eulerovu identitu názorněji:

  

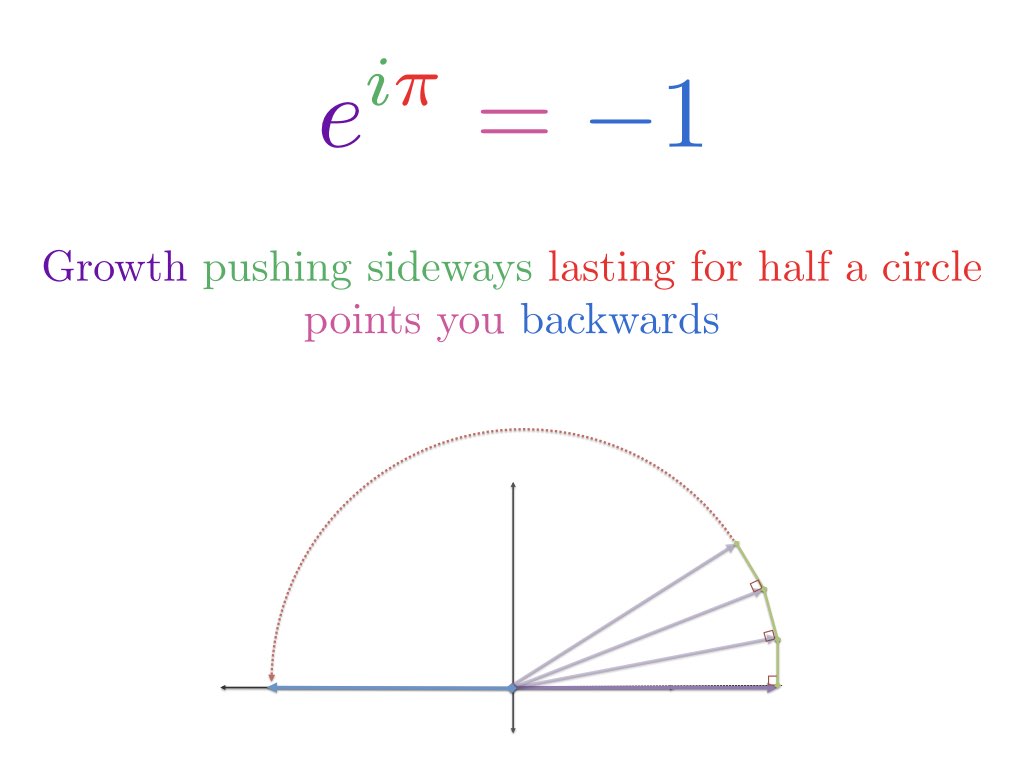
  Další příspěvky v této sérii

  1. Vizuální, intuitivní průvodce imaginárními čísly
  2. Intuitivní aritmetika s komplexními čísly
  3. Pochopení, proč funguje komplexní násobení
  4. Intuitivní průvodce úhly, stupňů a radiánů
  5. Intuitivní pochopení Eulerova vzorce
  6. Interaktivní průvodce Fourierovou transformací
  7. Intuitivní průvodce konvolucí
  8. Intuitivní pochopení sinusových vln
  9. Intuitivní průvodce lineární algebrou
  10. Intuice programátora pro násobení matic
  11. Imaginární násobení vs. Imaginární exponenty