V tipu měsíce (TOTM) za listopad 2011 jsme představili výpočty kompresoru v případové studii. Porovnali jsme výsledky rigorózní metody s hodnotami ze zkrácených metod. Rigorózní metoda byla založena na stavové rovnici typu Soave-Redlich-Kwong (SRK) pro výpočet potřebných entalpií a entropií. Entalpie a entropie se používají k určení potřebného výkonu a teplot při vybíjení. Výsledky ukázaly, že přesnost zkrácené metody je citlivá na hodnotu poměru tepelné kapacity ideálního stavu plynu, k.

Z hlediska samotného výpočtu je výpočet výkonu citlivý zejména na specifikaci hmotnostního průtoku, sací teploty a tlaku a výtlačné teploty a tlaku. Kompresor bude pracovat při různých hodnotách veličin ovlivňujících jeho výkon. Nejobtížnější částí výpočtu kompresoru je tedy specifikace rozumného rozsahu jednotlivých veličin, nikoli samotný výpočet. Odkaz zdůrazňuje, že použití jediné hodnoty pro každou proměnnou není správným způsobem vyhodnocení kompresního systému.

Obvykle se termodynamické výpočty provádějí pro ideální (vratný) proces. Výsledky reverzibilního procesu se pak přizpůsobí reálnému světu pomocí termodynamické účinnosti. V procesu komprese existují tři ideální procesy, které lze vizualizovat: 1) izotermický proces (PV1=C1), 2) izentropický proces (PVk=C2) a 3) polytropický proces (PVn=C3). Kterýkoli z těchto procesů lze vhodně použít jako základ pro vyhodnocení požadavků na kompresní výkon buď ručním, nebo počítačovým výpočtem. Izotermický proces se však jako základ používá zřídka, protože běžný průmyslový proces komprese neprobíhá ani přibližně při konstantní teplotě.

Všimněte si, že společnost Dresser Rand se poměrně hodně zabývá kompresí „při téměř konstantní teplotě“, zejména pro kompresi CO2 z ventilačních komínů. Podrobnosti viz:

V tomto TOTM si ukážeme, jak určit účinnost kompresoru z naměřeného průtoku, složení, sací a výtlačné teploty a tlaku. Uvádíme rigorózní výpočet založený na stavové rovnici a zkrácenou metodu a porovnáváme výsledky.

Účinnost kompresoru

Účinnost kompresoru se liší podle typu, velikosti a výkonu kompresoru. Lze je určit (dodatečně) pouze zkouškou kompresoru, ačkoli výrobci kompresorů mohou obvykle poskytnout dobré odhady. Pro účely plánování se v referencích uvádějí následující hodnoty celkové efficience:

Tabulka 1. Celkové účinnosti kompresorů

Odkaz uvádí, že tyto celkové efficience zahrnují tření plynu uvnitř kompresoru, mechanické ztráty (ložiska, těsnění, převodovka atd.) a ztráty převodovky. Mechanická efficience se liší podle velikosti a typu kompresoru, ale 95 % je užitečné číslo pro plánování. Při výpočtu výšky kompresoru a výstupní teploty se použije izentropická nebo polytropická efficience (izentropická efficience se někdy nazývá adiabatická efficience). Přičtením 3-4 % efficience (mechanické ztráty) k celkové efficienci v tabulce 1 získáme obecně dobrý odhad termodynamické efficience .

Pro vyhodnocení výkonu stávajícího kompresoru je cílem vypočítat účinnost kompresoru (η) a potřebný výkon.

Známé a naměřené vlastnosti jsou:

a. Objemový průtok plynu za standardních podmínek (qS) nebo hmotnostní průtok plynu ()

b. Složení plynu (zi)

c. Tlak v sání (P1) a teplota (T1)

d. Výtlačný tlak (P2) a teplota (T2)

Odhad účinnosti – rigorózní metoda

Srdcem každého komerčního softwaru pro simulaci proudění v procesu je stavová rovnice. Vzhledem k jejich jednoduchosti a relativní přesnosti se používá kubická EOS, například Soave Redlich-Kwong (SRK) nebo Peng-Robinson. Tyto rovnice se používají k výpočtu rovnováhy par a kapalin (VLE), entalpie (h) a entropie (s). Se správnými binárními interakčními koeficienty jsou výsledky simulace procesu těchto dvou rovnic prakticky stejné. Proto je v této práci použita pouze SRK.

Izentropická účinnost je definována vztahem

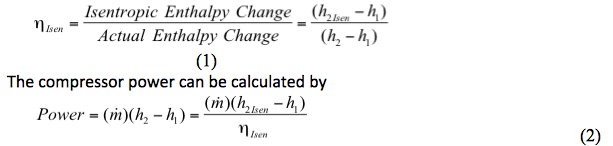
Kde:

ηIsen = izentropická účinnost

h1 = sací entalpie vypočtená při P1, T1 a složení (zi)

h2 = výtlačná entalpie vypočtená při P2, T2, a složení (zi)

h2Isen = Izentropická výtlačná entalpie při P2 (nebo T2), S2Isen =S1 a složení (zi)

= Hmotnostní průtok

Výpočet účinnosti nebo výkonu kompresoru zahrnuje dva kroky

1. Určení ideální nebo izentropické (reverzibilní a adiabatické) změny entalpie (h2Isen-h1) kompresního procesu.

2. Určení skutečné změny entalpie (h2-h1).

Krokový výpočet na základě EOS:

a. Předpokládejte ustálený stav, tj.

b. Předpokládejte, že složení krmiva zůstane nezměněno

c. Vypočítejte sací entalpii h1=f(P1, T1 a zi) a entropii s1=f(P1, T1 a zi) pomocí EOS

d. Předpokládejte izentropický proces a stanovte s2Isen = f (P2, T2Isen, zi) = s1 = f (P1, T1, zi).

e. Vypočítejte ideální entalpii (h2Isen) při podmínce vybití pro známé zi, T2 (nebo P2) a s2Isen.

f. Vypočítejte skutečnou entalpii (h2) při stavu výboje pro známé zi, T2 a P2.

g. Vypočítejte izentropickou účinnost podle rovnice 1: µIsen = (h2Isen – h1)/(h2 – h1)

h. Výpočet výkonu podle rovnice 2:

Odhad účinnosti – zkrácená metoda

Exponent izentropické dráhy (k) nebo poměr tepelné kapacity ideálního plynu (k=CP/CV) lze vypočítat pomocí korelace uvedené v TOTM z května 2013:

Kde:

T = teplota, K (°R)

= relativní hustota plynu; poměr molekulové hmotnosti plynu k molekulové hmotnosti vzduchu

A = 0.000272 (0.000151)

Skutečnou teplotu výboje na základě izentropické dráhy lze odhadnout pomocí

Řešení izentropické účinnosti,

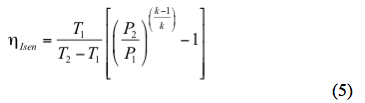
Podobně lze skutečnou teplotu výboje na základě polytropické dráhy odhadnout (ηPoly) pomocí:

Izentropická výška se vypočítá podle vzorce

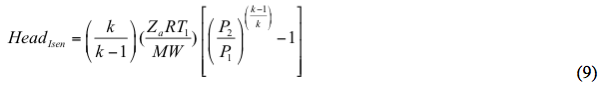
Podobně, polytropická hlava se vypočítá podle vztahu

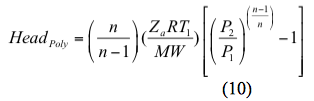
Pro izentropický (vratný a adiabatický) proces se výkon vypočítá podle vztahu

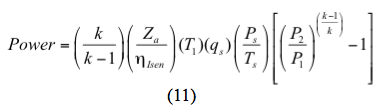
Nebo pro polytropický proces se výkon vypočítá podle vztahu

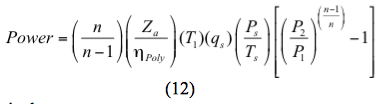
Alternativně:

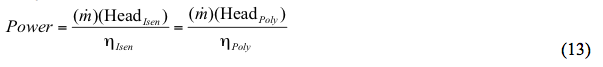
Kde:

Hlava = výška kompresoru, m (ft)

Výkon = výkon kompresoru, kW (HP)

R = univerzální plynová konstanta, 848 kg-m/(kmol-K) nebo (1545 ft-lbf/(lbmol-°R))

PS = tlak za standardních podmínek, kPa (psia)

P1 = sací tlak, kPa (psia)

P2 = výstupní tlak, kPa (psia)

TS = teplota standardního stavu, K (°R)

T1 = teplota sání, K (°R)

T2 = teplota výstupu, K (°R)

qS = objemová rychlost plynu za standardních podmínek, Sm3/d (scf/den)

Za = průměrný faktor stlačitelnosti plynu = (Z1+Z2)/2

Z1 = faktor stlačitelnosti plynu při sacích podmínkách

Z2 = faktor stlačitelnosti plynu při výtlačných podmínkách

MW = molekulová hmotnost plynu

Výpočet výkonu by měl být proveden pro každý stupeň komprese a poté sečten pro všechny stupně připojené k jednomu pohonu.

Krokový výpočet pro zkrácenou metodu

a. Vypočítejte izentropický exponent (k) podle rovnice 3 s použitím průměrné teploty definované vztahem T = (T1+3T2)/4. Tento tvar průměrné teploty byl definován za účelem dosažení lepší shody mezi výsledky rigorózní a zkrácené metody

b. Vypočítejte izentropickou účinnost (ηIsen) podle rovnice 5.

c. Vypočítejte polytropický koeficient (n) podle rovnice 7.

d. Vypočítejte polytropickou účinnost (ηPoly) podle rovnice 8.

e. Vypočítejte izentropické a polytropické hlavice podle rovnic 9 a 10.

f. Vypočítejte potřebný výkon na jeden stupeň podle rovnice 11 nebo 12.

Případová studie

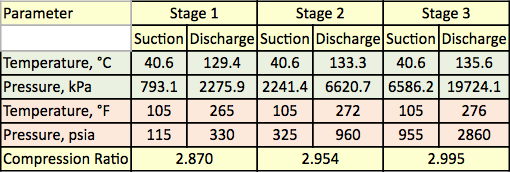
Směs zemního plynu se stlačuje pomocí třístupňového odstředivého kompresoru. Schéma průběhu procesu je znázorněno na obrázku 1. Pro každý stupeň jsou v tabulce 1 uvedeny naměřené hodnoty tlaku a teploty. Naměřené složení vstupního plynu, průtoky a vypočtená molekulová hmotnost a relativní hustota jsou uvedeny v tabulce 2.

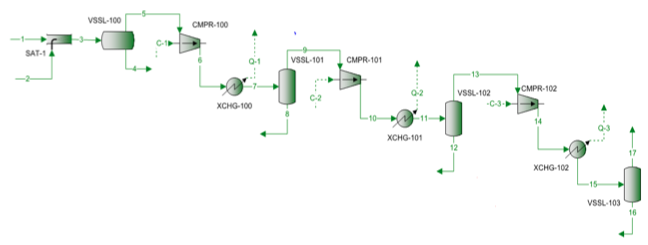
Obrázek 1. Průběhový diagram procesu pro třístupňovou kompresi

Tabulka 1. Naměřená teplota a tlak pro tři stupně komprese

Tabulka 2. Analýza plynu a průtok pro tři stupně komprese

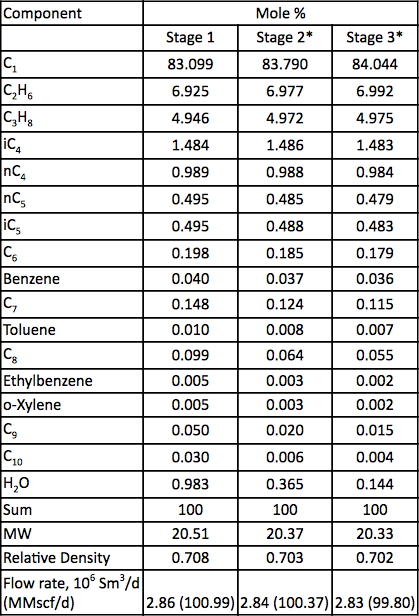
* Vypočtené

Výsledky a diskuse

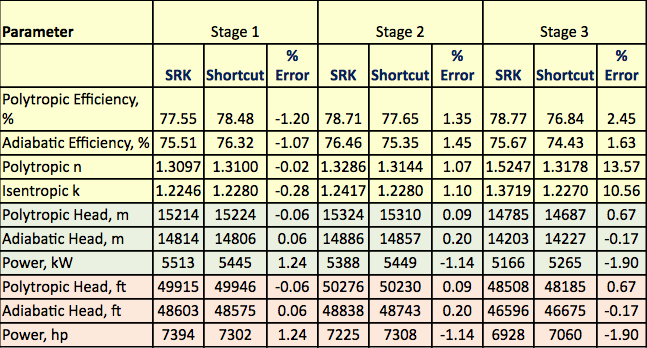
Procesní schéma znázorněné na obrázku 1 bylo simulováno softwarem ProMax pro provedení rigorózních výpočtů pomocí systému SRK EOS. Program vypočítal polytropickou a izentropickou účinnost, hlavy a kompresní výkon. Program rovněž vypočítal exponent izentropické cesty (k) a exponent polytropické cesty (n). Tyto vypočtené výsledky jsou uvedeny v tabulce 2 pro všechny tři stupně pod hlavičkami SRK. Výpočty provedené programem ProMax jsou velmi podobné postupným krokům a až h popsaným v rigorózní části. V tabulce 2 jsou rovněž uvedeny výsledky zkráceného výpočtu pro odpovídající hodnoty pod zkrácenou hlavičkou. Zkrácené výpočty jsou založeny na postupných výpočtech a až f popsaných v oddíle o zkrácené metodě. Procentuální chyby mezi rigidní metodou a zkrácenými metodami pro každou etapu jsou rovněž uvedeny v tabulce 2. Z tabulky 2 vyplývá, že pro etapy 1 a 2 bylo dosaženo vynikající shody. Větší odchylky jsou však pozorovány u izetropických a polytropických exponentů etapy 3 v důsledku vysokotlakého provozu, který se příliš odchýlil od podmínek ideálního stavu plynu.

Tabulka 3. Shrnutí rigorózních a zkrácených výpočtů

Závěry

Tabulka 2 ukazuje, že mezi zkrácenými a rigorózními výsledky je dobrá shoda. Rozdíly mezi výsledky rigorózní a zkrácené metody pro výpočty zařízení a účely plánování jsou zanedbatelné. U fáze 3 je v důsledku vysokotlakého provozu a přílišné odchylky od stavu ideálního plynu pozorována větší chyba u izentropického exponentu (k).

Vypočtený izentropický exponent (k) v ProMaxu není poměrem tepelné kapacity ideálního stavu plynu (CP/CV). Je to hodnota izentropického exponentu, která je nutná k získání izentropické dráhy od vstupu k výstupu. Jeho hodnota se vypočítá jako integrace této cesty. Jedná se tedy o jakousi „průměrnou“ hodnotu, která představuje skutečnou izentropickou dráhu. Pro ideální plyny by se hodnota rovnala poměru (CP/CV).

Tato chyba v „k“ také ilustruje, jak je důležité při objednávání zkoušky výkonnosti specifikovat, jaká korelace se má použít (tj. další podrobnosti naleznete v ASME PTC-10), aby se zákazník a dodavatel při dalším postupu shodli, pokud jde o molekulovou hmotnost (MW) a k pro zkoušenou kapalinu. Další podrobnosti naleznete v referenci a v TOTM ze srpna a září 2010 .

Možná stojí za zmínku také to, že při trendu „n“ a polytropické účinnosti pro vyhodnocení stavu stroje vnáší relativní přesnost měřicích přístrojů/zařízení (snímače teploty a tlaku) a mapování výkonu kompresoru na původní výkonovou křivku (skutečný objemový průtok plynu v závislosti na otáčkách) do tohoto denního vyhodnocení mnoho potenciálních chybných zdrojů.

Všimněte si, že přesnost zkrácených metod závisí na hodnotách k a n. Definice průměrné teploty ve zkrácené metodě byla upravena, aby se dosáhlo lepší shody mezi exponentem izentropické dráhy (k) vypočteným rigorózní metodou.

Chcete-li se dozvědět více o podobných případech a o tom, jak minimalizovat provozní problémy, doporučujeme navštívit naše kurzy G4 (Klimatizace a zpracování plynu), PF4 (Zařízení pro těžbu a zpracování ropy), ME46 (Kompresorové systémy – mechanický návrh a specifikace) a ME44 (Základy čerpacích a kompresorových systémů),

PetroSkills nabízí konzultační expertízu na toto téma a mnoho dalších. Více informací o těchto službách naleznete na našich webových stránkách http://petroskills.com/consulting nebo nám napište na [email protected].

Dr. Mahmood Moshfeghian

Odkazy:

3. Soave, G., Chem. Eng. Sci., Vol. 27, s. 1197-1203, 1972.

4. Peng, D. Y., and Robinson, D. B., Ind. Eng. Chem. Fundam., Vol. 15, p. 59, 1976.

5. ProMax 3.2, Bryan Research and Engineering, Inc, Bryan, Texas, 2014.

6. ASME PTC-10, „Performance test Code on Compressors and Exhausters“, 1997.

7. Honeywell, J. „Important Aspects of Centrifugal Compressor Testing-Part 1“, Tip měsíce, srpen 2010

8. Honeywell, J. „Important Aspects of Centrifugal Compressor Testing-Part 2“, Tip měsíce, září 2010

.