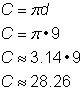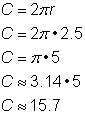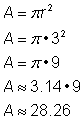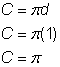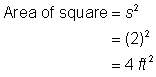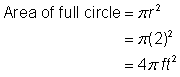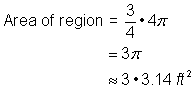Kružnice
Cíl(e) výuky
– Určit vlastnosti kružnic.
– Určit obvod kružnice.
– Určit obsah kruhu.
– Určit obsah a obvod složených geometrických útvarů.
Úvod
Kruhy jsou běžným útvarem. Vidíte je všude – kola na autě, frisbee prolétávající vzduchem, kompaktní disky přenášející data. To všechno jsou kružnice.
Kružnice je dvourozměrný útvar stejně jako mnohoúhelníky a čtyřúhelníky. Kruhy se však měří jinak než tyto ostatní útvary – dokonce pro jejich popis musíte používat některé odlišné termíny. Podívejme se na tento zajímavý útvar.
Vlastnosti kružnic
Kruh představuje množinu bodů, které jsou všechny stejně vzdálené od pevného středového bodu. Tento pevný bod se nazývá střed. Vzdálenost od středu kružnice k libovolnému bodu na kružnici se nazývá poloměr.
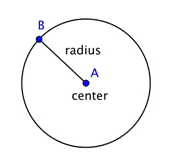
Když dva poloměry (množné číslo poloměru) spojíme dohromady a vytvoříme úsečku napříč kružnicí, dostaneme průměr. Průměr kružnice prochází středem kružnice a má koncové body na samotné kružnici.
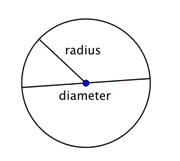
Průměr libovolné kružnice je dvojnásobek délky poloměru této kružnice. Lze jej znázornit výrazem 2r neboli „dvojnásobek poloměru“. Znáte-li tedy poloměr kruhu, můžete jej vynásobit číslem 2 a zjistit průměr; to také znamená, že znáte-li průměr kruhu, můžete jej vydělit číslem 2 a zjistit poloměr.
|
Příklad |
||
|
Problém |
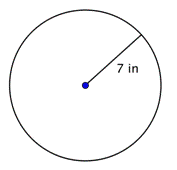
Zjistěte průměr kruhu.
|
|
|
d = 2r d = 2(7) d = 14 |
Průměr je dvojnásobek poloměru neboli 2r. Poloměr této kružnice je 7 palců, takže průměr je 2(7) = 14 palců. |
|
|
Odpověď |
Průměr je 14 palců. |
|
|
Příklad |
||
|
Problém |
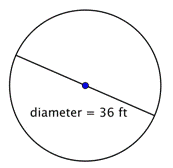
Zjistěte poloměr kruhu.
|
|
|
|
Poloměr je polovina průměru, tedy |
|
|
Odpověď |
Poloměr je 18 stop. |
|
Obvod
Vzdálenost kolem kruhu se nazývá obvod. (Připomeňme, že vzdálenost kolem mnohoúhelníku je obvod.)
Jednou zajímavou vlastností kruhů je, že poměr obvodu kruhu a jeho průměru je pro všechny kruhy stejný. Nezáleží na velikosti kruhu, poměr obvodu a průměru bude stejný.
Několik skutečných měření různých předmětů je uvedeno níže. Měření jsou uvedena s přesností na milimetr nebo čtvrt palce (v závislosti na použité měrné jednotce). Podívejte se na poměr obvodu a průměru u každého z nich – i když jsou předměty různé, poměr je u každého z nich přibližně stejný.
|
Předmět |
Obvod (C) (zaokrouhleno na nejbližší setinu) |
.
Průměr (d) |
Rozměr |
|
Šálek |
253 mm |
79 mm |
|
|
Čtvrtka |
84 mm |
27 mm |
|
|
Miska |
37.25 in |
11,75 in |
|
Obvod a průměr jsou přibližné míry, protože neexistuje přesný způsob, jak tyto rozměry přesně změřit. Kdybyste je však byli schopni změřit přesněji, zjistili byste, že poměr ![]() by se u každé z uvedených položek posunul směrem k hodnotě 3,14. To by znamenalo, že se poměr
by se u každé z uvedených položek posunul směrem k hodnotě 3,14. To by znamenalo, že se poměr ![]() posunul směrem k hodnotě 3,14. Matematický název pro poměr
posunul směrem k hodnotě 3,14. Matematický název pro poměr ![]() je pí a je reprezentován řeckým písmenem
je pí a je reprezentován řeckým písmenem ![]() .
.
![]() je nekonečné, neopakující se desetinné číslo, takže ho nelze vypsat celé. Prvních deset číslic
je nekonečné, neopakující se desetinné číslo, takže ho nelze vypsat celé. Prvních deset číslic ![]() je 3,141592653; často se zaokrouhluje na 3,14 nebo se odhaduje jako zlomek
je 3,141592653; často se zaokrouhluje na 3,14 nebo se odhaduje jako zlomek ![]() . Všimněte si, že jak 3,14, tak
. Všimněte si, že jak 3,14, tak ![]() jsou přibližnými hodnotami čísla
jsou přibližnými hodnotami čísla ![]() a používají se při výpočtech, kde není důležitá přesnost.
a používají se při výpočtech, kde není důležitá přesnost.
Jelikož víte, že poměr obvodu a průměru (neboli ![]() ) je shodný pro všechny kružnice, můžete toto číslo použít k určení obvodu kružnice, pokud znáte její průměr.
) je shodný pro všechny kružnice, můžete toto číslo použít k určení obvodu kružnice, pokud znáte její průměr.
![]() =
= ![]() , takže C =
, takže C = ![]() d
d
Jelikož d = 2r, pak C = ![]() d =
d = ![]() (2r) = 2
(2r) = 2![]() r.
r.
Obvod kruhu
Chcete-li zjistit obvod (C) kruhu, použijte jeden z následujících vzorců:
Znáte-li průměr (d) kruhu: ![]()
Znáte-li poloměr (r) kruhu: ![]()
|
Příklad |
||
|
Problém |
Zjistěte obvod kruhu.
|
|
|
|
Pro výpočet obvodu při průměru 9 palců použijte vzorec Protože pro |
|
|
Odpověď |
Obvod je 9 |
|
|
Příklad |
||
|
Problém |
Zjistěte obvod kruhu o poloměru 2. Obvod kruhu je 2 cm.5 yardů. |
|
|
|
Pro výpočet obvodu kruhu daného poloměrem 2,5 yardů použijte vzorec |
|
|
Odpověď |
Obvod je 5 |
|
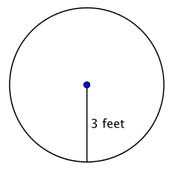
Kruh má poloměr 8 palců. Jaký je jeho obvod zaokrouhlený na nejbližší palec?
A) 25 palců
B) 50 palců
C) 64 palců2
D) 201 palců
Obvod
![]() je v geometrii důležité číslo. Již jste ho použili k výpočtu obvodu kruhu. Číslo
je v geometrii důležité číslo. Již jste ho použili k výpočtu obvodu kruhu. Číslo ![]() použijete i při zjišťování plochy kruhu.
použijete i při zjišťování plochy kruhu.
Plocha kruhu
Pro zjištění plochy (A) kruhu použijte vzorec: ![]()
|
Příklad |
||
|
Problém |
Najděte obsah kruhu.
|
|
|
|
Pro zjištění plochy této kružnice použijte vzorec Nezapomeňte odpověď zapsat v jednotkách čtverce, protože zjišťujete plochu. |
|
|
Odpověď |
Plocha je 9 |
|
Knoflík má průměr 20 milimetrů. Jaká je plocha knoflíku? Jako přibližnou hodnotu použijte 3,14 ![]() .
.
A) 62,8 mm
B) 314 mm2
C) 400 mm2
D) 1256 mm2
Složené útvary
Když už víte, jak vypočítat obvod a obsah kruhu, můžete tyto znalosti použít k nalezení obvodu a obsahu složených útvarů. Trik při řešení těchto typů úloh spočívá v tom, že určíš útvary (a části útvarů) ve složeném obrazci, vypočteš jejich jednotlivé rozměry a pak je sečteš.
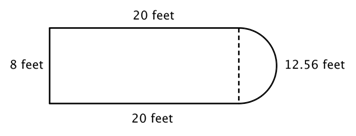
Podívej se například na obrázek níže. Je možné zjistit jeho obvod?“
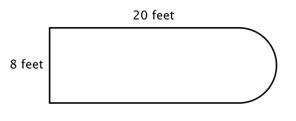
Prvním krokem je identifikovat jednodušší útvary v rámci tohoto složeného obrazce. Můžeš ho rozložit na obdélník a půlkruh, jak je znázorněno na obrázku níže.
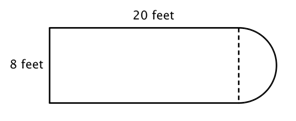
Už víš, jak najít obvod obdélníku, a víš, jak najít obvod kruhu. Zde je obvod tří pevných stran obdélníku 8 + 20 + 20 = 48 stop. (Všimni si, že do obvodu složeného obrazce se sečtou pouze tři strany obdélníku, protože druhá strana není na okraji; je zakryta půlkružnicí!“
Pro zjištění obvodu půlkružnice použij vzorec ![]() s průměrem 8 stop a z výsledku odečti polovinu. Obvod půlkruhu je
s průměrem 8 stop a z výsledku odečti polovinu. Obvod půlkruhu je ![]() , tedy přibližně 12,56 stopy, takže celkový obvod je přibližně 60,56 stopy.
, tedy přibližně 12,56 stopy, takže celkový obvod je přibližně 60,56 stopy.
|
Příklad |
||
|
Problém |
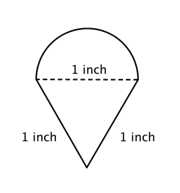
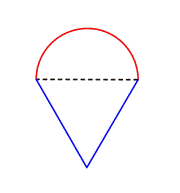
Zjistěte obvod (s přesností na setiny) složeného obrazce, který se skládá z půlkruhu a trojúhelníku.
|
|
|
|
Označte menší útvary uvnitř složeného obrazce. Tento obrazec obsahuje půlkruh a trojúhelník. |
|
|
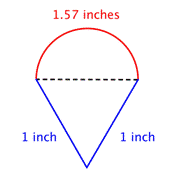
Průměr (d) = 1
Obvod půlkruhu = |
Zjistěte obvod kružnice. Potom vydělte dvěma a zjistíte obvod půlkruhu. |
|
|
|
|
Zjistěte celkový obvod sečtením obvodu půlkruhu a délek obou ramen. Protože naše měření obvodu půlkruhu je přibližné, bude i obvod přibližný. |
|
Odpověď |
Přibližně 3. Jaký je obvod půlkruhu?57 palců |
|
|
Příklad |
||
|
Problém |
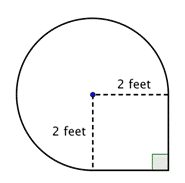
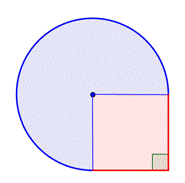
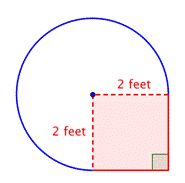
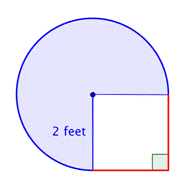
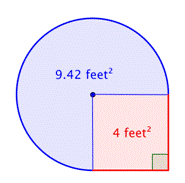
Zjistěte plochu složeného obrazce, složeného ze tří čtvrtin kruhu a čtverce, s přesností na setiny.
|
|
|
|
Určete menší útvary uvnitř složeného obrazce. Tento obrazec obsahuje kruhovou oblast a čtverec. Pokud zjistíte plochu každého z nich, můžete zjistit plochu celého útvaru. |
|
|
|
Zjistěte plochu čtverce. |
|
|
|
|
Najděte plochu kruhové oblasti. Poloměr je 2 stopy. Všimněte si, že oblast tvoří |
|
|
4 stopy2 + |
Přičti obě oblasti k sobě. Vzhledem k tomu, že vaše měření plochy kruhu je přibližné, bude i plocha obrázku přibližná. |
|
Odpověď |
Plocha je přibližně 13,42 m².42 stop2. |
|
Jaká je plocha (s přesností na setiny) níže uvedeného obrázku? (Obě zaoblené oblasti jsou půlkruhy.)
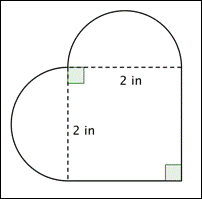
A) 16,56 in2
B) 7,14 in2
C) 4 in2
D) 3,14 in2
Souhrn
Kruhy jsou důležitý geometrický útvar. Vzdálenost kolem kruhu se nazývá obvod a vnitřní prostor kruhu se nazývá plocha. Výpočet obvodu a plochy kruhu vyžaduje číslo zvané pí (![]() ), což je nekonečné, neopakující se desetinné číslo. Pí se často aproximuje hodnotami 3,14 a
), což je nekonečné, neopakující se desetinné číslo. Pí se často aproximuje hodnotami 3,14 a ![]() . Obvod nebo obsah složených útvarů – včetně útvarů, které obsahují kruhové výseče – můžete zjistit tak, že v případě potřeby použijete vzorce pro obvod a obsah.
. Obvod nebo obsah složených útvarů – včetně útvarů, které obsahují kruhové výseče – můžete zjistit tak, že v případě potřeby použijete vzorce pro obvod a obsah.
.