
Galileo je často považován za otce moderní vědy. Byl to on, kdo spojil principy experimentu, teorie a matematiky dohromady do standardního rámce. Pravděpodobně více než kdokoli jiný byl Galileo osobou zodpovědnou za rozvoj moderní vědy.
Říká se, že Galileo spustil ze šikmé věže v Pise dvě ocelové koule o různých hmotnostech, ale ze stejného materiálu, a ty dopadly ve stejnou dobu. Na tomto experimentu je pozoruhodné, že zavedl novou metodu vědecké práce, při níž se provádí experiment k ověření hypotézy. Ukázal, že nestačí si jen myslet, že je něco pravda, ale musíme to také dokázat.

Galileo objevil zajímavý paradox v době, kdy byl vedoucím katedry matematiky na univerzitě v Pise.
Definice: Paradox, známý také jako antinomie, je logicky si odporující tvrzení nebo tvrzení, které je v rozporu s očekáváním. (Wikipedie). (Řecky: „para“ = mimo, „doxa“ = víra)
Galileův paradox se týkal určení, zda jsou dvě množiny obsahující nekonečně mnoho objektů navzájem ekvivalentní. Například nechť P je množina celých kladných čísel, kde P = {0,1,2,3,…} a E je množina sudých čísel, kde E = {0,2,4,6,…}. Galileo tvrdil, že velikosti těchto dvou množin budou stejné, protože každé kladné celé číslo z množiny P můžeme spárovat se sudými čísly z množiny E.

Jak je tedy možné, že velikosti obou množin jsou stejné, když se v E vyskytuje „menší“ číslo? Tento problém byl nazván Galileův paradox a odstartoval novou debatu o pojmu nekonečna.
Po Galileovi se jeho žák Evangelista Torricelli stal vedoucím katedry matematiky na univerzitě v Pise. Možná jste o něm slyšeli díky jeho pracím o atmosférickém tlaku a vynálezu barometru. Protože se Toricelli zajímá také o matematiku, klade si otázku:
Může mít objekt konečný objem a nekonečný povrch? V první řadě se taková věc zdá většině z nás nepravděpodobná. Matematika nám však říká, že se taková věc může stát. Torricelli si na svou otázku odpověděl sám a objevil Toricelliho trubku, jejíž povrch je nekonečný, ale objem konečný. Svůj objev vnímal jako „neuvěřitelný“ paradox.
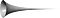
Mimochodem, ve filozofii matematiky platí zásadní pravidlo: Ať se zabýváte jakoukoli epochou filozofie nebo matematiky, souvisí to s historií, kulturou a náboženstvím dané oblasti. Proto se Toricelliho trubce říká také Gabrielův roh. Odkazuje se zde na Bibli, protože křesťané věří, že v soudný den na tento roh zatroubí anděl Gabriel.
Jak tedy Toricelliho trubka vzniká? Všichni víme, jak se vykresluje graf y=x. Pokud místo toho vykreslíme graf rovnice y=1/x, kde x je větší nebo rovno 1, bude graf vypadat takto:
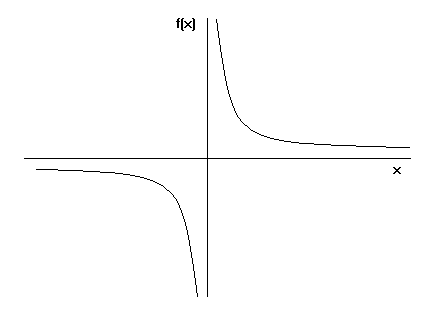
Když vezmeme graf y=1/x a otočíme ho kolem osy x, vidíme Toricelliho trubici.

Naštěstí máme v rukou matematické vzorce pro výpočet plochy a objemu Toricelliho trubice. Když použijeme níže uvedený integrační vzorec pro objem trubky, dostaneme konečnou velikost.
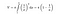
Když však použijeme integrační vzorec pro plochu trubky, tentokrát se její plocha stane nekonečnou. Není tento výsledek zajímavý?“
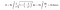
Protože objem Toricelliho trumpety je konečný, můžeme ji naplnit konečným množstvím barvy. Předpokládejme například, že její objem 100 litrů. Půjdu do obchodu Home Depot, koupím 100 litrů barvy a naplním ji. Zajímavé však je, že oněmi 100 litry barvy natřu nekonečnou plochu. Většina lidí dnes tento paradox nazývá „paradox malíře“.
Houstone, máme tu problém! Situace, která je v praxi nemožná, se v matematice stává možnou. Jak tedy může být Torricelliho trubka skutečná? Nebo jak můžeme přesně shodovat všechny prvky množin, zatímco jedna z množin je podmnožinou jiné v Galileově příkladu?“
Důvodem všech těchto rozporů je to, že pojem nekonečna není podobný jiným pojmům, které známe, a to mnoho lidí mate. Galileo ke svému paradoxu říká,
„Ano, příteli, existuje nekonečno. Je zbytečné proti němu něco namítat. Množiny, kterými se zabývám, jsou příklady uzavřených množin, které zahrnují nekonečno. Začínají v bodě a pokračují do nekonečna, a přesto jsou to stále množiny. Mé komentáře a pojmy týkající se nekonečna se však musí lišit od těch, které bych použil pro konečné veličiny. Pokud se zabýváte konečnými veličinami, můžete říci, že 3 kila jsou méně než 5 kilo nebo že 32 metrů je delší než 7 metrů. Ale pokud jde o nekonečno, nemůžete říci, že toto nekonečno je větší, menší nebo rovné tomuto.“
Toto bylo Galileovo řešení 16. století.
Naneštěstí Galileovo řešení odstartovalo novou debatu o nekonečnu. Matematici a filozofové se nemohli shodnout na konkrétní odpovědi, dokud se Cantor nepodělil o svou „teorii množin“, kterou se dnes žáci učí na základní škole.
Můžeme periodicky historizovat vývoj myšlenky nekonečna. Poprvé se objevila u eleatů, což byla předsokratovská filozofická škola založená Parmenidem na počátku 5. století př. n. l. ve starověkém městě Elea. V této škole působili tři velcí filozofové, například Zenón, Xenofanés a Parmenidés. V této škole byla přijata filozofie, že existence je jediná a neexistuje pluralita. Zenón se u eleatů proslavil svými paradoxy o nekonečnu. Později v roce 300 př, Kr. vznikl Aristotelés, který navrhl dvojici pojmů vysvětlujících Zenónovy paradoxy, kterými byly potenciální nekonečno a aktuální nekonečno.
Potenciální nekonečno je skupina čísel nebo skupina „věcí“, která pokračuje, aniž by skončila, pokračuje nebo se opakuje stále dokola bez rozpoznatelného koncového bodu.
Skutečné nekonečno zahrnuje nikdy nekončící množiny nebo „věci“ v prostoru, který má začátek a konec; je to řada, která je technicky „ukončená“, ale skládá se z nekonečného počtu členů.
Aristoteles se domníval, že skutečné nekonečno neexistuje. Tato Aristotelova představa ovládala světovou filozofii až do roku 1600. Poté filozofové jako Cusa a Bruno tvrdili, že skutečné nekonečno existuje, ale nemůžeme mu dát smysl. Po Cusovi a Brunovi se do tématu zapojil velký myslitel Spinoza.
Spinoza tvrdil, že můžeme pochopit pojem nekonečna a seřadit je podle velikosti. Zároveň však prohlásil, že je nedokáže spočítat. Například dokázal sečíst 3 s 5, ale nedokázal sečíst jedno nekonečno s druhým.
Nakonec se na závěr těchto debat objevil krásný muž Georg Cantor, který objevil teorii množin, která je dodnes základem matematiky. Svou teorií množin stanovil poslední bod v diskusích o nekonečnu.
Ukázal nám, že nekonečná množina bude větší nebo menší než jiná nekonečná množina. Dále Cantor tvrdil, že můžeme nekonečné množiny sčítat a násobit. Do té doby se lidé řídili Aristotelovými představami o nekonečnu. Podle Aristotela kdybychom číslo 3 vynásobili nekonečnem, bylo by opět nekonečné. Nekonečno by pohltilo všechno. Na základě toho tvrdil, že by existovalo pouze potenciální nekonečno, nikoli skutečné nekonečno.
Kantor nám však pomocí teorie množin dokázal opak Aristotelovy představy. Pokud k nekonečné množině přidáme jedničku, už to nebude stejná množina. Pokusil se porovnat nekonečna. Cantor například dokázal, že množina všech funkcí z (0,1)→ℕ je spočetná. Definoval tedy jednosměrnou a onto funkci z intervalu (0,1) na přirozená čísla.
Jinými slovy dokázal, že všechna přirozená čísla se vejdou mezi 0 a 1, protože mezi 0-1 bylo nekonečně racionálních čísel a tato nekonečna lze spárovat. Pak udělal něco ještě nebezpečnějšího než nalezení dvou stejných nekonečen. Porovnal nekonečnost reálných čísel s nekonečností přirozených čísel a zjistil, že nekonečnost reálných čísel je větší než ta druhá. Dokonce se podíval na svůj důkaz a řekl svému příteli Dedekindovi: „Vidím to, ale ani já tomu nemohu uvěřit…“
Cantor byl také matematik s velmi vážnými filozofickými a náboženskými zájmy. Při vývoji teorie množin prohlásil: „Teorii množin mi nadiktoval Bůh.“
Teorie množin nebyla v době svého vzniku široce přijímána. Firmy dokonce Cantora nenajímaly na žádnou práci. Matematik Henri Poincaré jednou řekl: „Myšlenky tohoto Cantora jsou zlou nemocí, která se lepí na límec matematiky. A matematika ho jednou vyléčí“. Cantor musel na čas odejít do psychiatrické léčebny a tam zemřel. Dnes ho však považujeme za génia.
Cantor byl osamělý muž na okraji nekonečna. Na začátku svého článku o nekonečných číslech citoval Bibli: „Vše, co je skryto, bude vyneseno na světlo.“