Vlastní čísla jsou speciální množina skalárů spojených s lineární soustavou rovnic (tj.e., maticovou rovnicí), které se někdy označují také jako charakteristické kořeny, charakteristické hodnoty (Hoffman a Kunze 1971), vlastní hodnoty nebo skryté kořeny (Marcus a Minc 1988, s. 144).

Určení vlastních hodnot a vlastních vektorů systému je nesmírně důležité ve fyzice a technice, kde je ekvivalentní diagonalizaci matic a objevuje se v takových běžných aplikacích, jako je analýza stability, fyzika rotujících těles a malých kmitů vibračních systémů, abychom jmenovali jen některé. Každé vlastní číslo je spárováno s odpovídajícím tzv. vlastním vektorem (nebo obecně s odpovídajícím pravým vlastním vektorem a odpovídajícím levým vlastním vektorem; u vlastních čísel neexistuje analogické rozlišení mezi levým a pravým).

Rozklad čtvercové matice na vlastní čísla a vlastní vektory je v této práci znám jako vlastní rozklad a skutečnost, že tento rozklad je vždy možný, pokud je matice složená z vlastních vektorů čtvercová, je známa jako věta o vlastním rozkladu.

Lanczosův algoritmus je algoritmus pro výpočet vlastních čísel a vlastních vektorů pro velké symetrické řídké matice.

Nechť je lineární transformace reprezentovaná maticí . Existuje-li vektor takový, že

(1)

pro nějaký skalár , pak se nazývá vlastní číslo s příslušným (pravým) vlastním vektorem .

Nechť je čtvercová matice

(2)

s vlastní hodnotou , pak příslušné vlastní vektory splňují

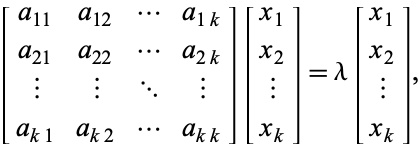(3)

což je ekvivalentní homogennímu systému

.

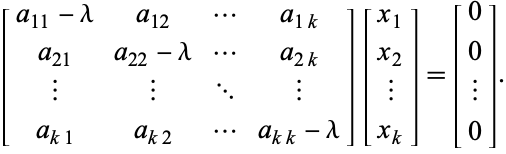(4)

Rovnici (4) lze kompaktně zapsat jako

(5)

kde je identická matice. Jak ukazuje Cramerovo pravidlo, lineární soustava rovnic má netriviální řešení, jestliže determinant mizí, takže řešení rovnice (5) je dáno vztahem

(6)

Tato rovnice je známá jako charakteristická rovnice a levá strana je známá jako charakteristický polynom.

Například pro matici , vlastní čísla jsou

(7)

která vznikají jako řešení matice

. charakteristikarovnice

(8)

Jestliže jsou všechny vlastní hodnoty různé, pak jejich zpětným dosazením získáme nezávislé rovnice pro složky každého příslušného vlastního vektoru a říká se, že systém je nedegenerovaný. Pokud jsou vlastní hodnoty násobně degenerované, pak se říká, že systém je degenerovaný a vlastní vektory nejsou lineárně nezávislé. V takových případech lze použít dodatečné omezení, že vlastní vektory musí být ortogonální,

(9)

kde je Kroneckerova delta, a získat tak dodatečné omezení, které umožní řešení pro vlastní vektory.

Vlastní čísla lze ve Wolframově jazyce vypočítat pomocí funkce Eigenvalues. Vlastní vektory a vlastní hodnoty lze vrátit společně pomocí příkazu Eigensystem.

Předpokládejme, že známe vlastní číslo pro

(10)

Přidáme-li k konstantu krát identitní matice,

(11)

takže nová vlastní čísla se rovnají starým plus . Vynásobíme-li konstantou

(12)

tak se nová vlastní čísla rovnají starým vynásobeným .

Nyní uvažujeme podobnostní transformaci . Nechť je determinant , pak

.

			(13)
			(14)
			(15)

takže vlastní čísla jsou stejná jako pro .