Oppimistavoitteet
- Ymmärtää elektroniorbitaalien kolmiulotteinen esitystapa
Orbitaali on Boorin radan kvanttimekaaninen jalostus. Toisin kuin hänen käsitteensä yksinkertaisesta ympyrästä\(r\), jolla on kiinteä säde, orbitaalit ovat matemaattisesti johdettuja avaruusalueita, joilla on erilaiset todennäköisyydet sisältää elektroni.
Ensimmäistä tapaa esittää elektronien todennäköisyysjakaumia havainnollistettiin aiemmin vedyn 1s-rata-alalla. Koska Ψ2 antaa todennäköisyyden löytää elektroni tietyssä tilavuudessa (kuten kuutiopikometrissä), Ψ2:n kuvaaja etäisyyden suhteen ytimestä (r) on todennäköisyystiheyden kuvaaja. 1s:n rata on pallosymmetrinen, joten todennäköisyys löytää 1s:n elektroni missä tahansa pisteessä riippuu vain sen etäisyydestä ytimestä. Todennäköisyystiheys on suurin \(\(r\) = 0\) (ytimessä) ja pienenee tasaisesti etäisyyden kasvaessa. Hyvin suurilla r:n arvoilla elektronin todennäköisyystiheys on hyvin pieni, mutta ei nolla.
Voidaan sitä vastoin laskea säteittäinen todennäköisyys (todennäköisyys löytää 1s elektroni etäisyydellä \(r\) ytimestä) laskemalla yhteen \(r\) todennäköisyydet sille, että elektroni on kaikissa pisteissä sarjassa x:ää pallonmuotoista kuorta, joiden säde on säde x r1, x r2, x r2, x r2, x r2, x r3, x rx, x x x, x x x rx. Käytännössä jaamme atomin hyvin ohuisiin samankeskisiin kuoriin, jotka muistuttavat sipulin kerroksia (kuva \(\PageIndex{1a}\)), ja laskemme todennäköisyyden elektronin löytymiselle jokaiselta pallokuorelta. Muistutetaan, että elektronin todennäköisyystiheys on suurin kohdassa \(r\) = 0 (kuva \(\(\PageIndex{1b}\)), joten pistetiheys on suurin kuvassa \(\(\PageIndex{1}\) olevan osan (a) pienimmillä pallomaisilla kuorilla.) Sitä vastoin kunkin pallonmuotoisen kuoren pinta-ala on \(4πr^2\), joka kasvaa hyvin nopeasti \(r\):n kasvaessa (kuva \(\(\PageIndex{1c}\)). Koska pallokuorien pinta-ala kasvaa nopeammin \(r\):n kasvaessa kuin elektronien todennäköisyystiheys pienenee, säteittäisen todennäköisyyden kuvaajassa on maksimi tietyllä \(r\)-etäisyydellä (kuva \(\(\PageIndex{1d}\)). Tärkeintä on, että kun \(r\) on hyvin pieni, pallokuoren pinta-ala on niin pieni, että kokonaistodennäköisyys löytää elektroni läheltä ydintä on hyvin pieni; ytimen kohdalla elektronin todennäköisyys häviää (kuva \(\(\PageIndex{1d}\)).


Fo\(r\) vetyatomin säteittäisen todennäköisyyden kuvaajassa huippu on pisteessä \(r\) = 0,529 Å (52,9 pm), joka on täsmälleen Bohin laskema säde fo\(r\) kiertoradalle n = 1. Tämä on myös Bohin laskema säde. Näin ollen kvanttimekaniikan avulla saatu todennäköisin säde on sama kuin klassisen mekaniikan avulla laskettu säde. Bohrin mallissa elektronin oletettiin kuitenkin olevan tällä etäisyydellä 100 prosenttia ajasta, kun taas Schrödingen\(r\) mallissa se on tällä etäisyydellä vain osan ajasta. Ero näiden kahden mallin välillä johtuu elektronin aaltomaisesta käyttäytymisestä\(r\) ja Heisenbergin epävarmuusperiaatteesta.
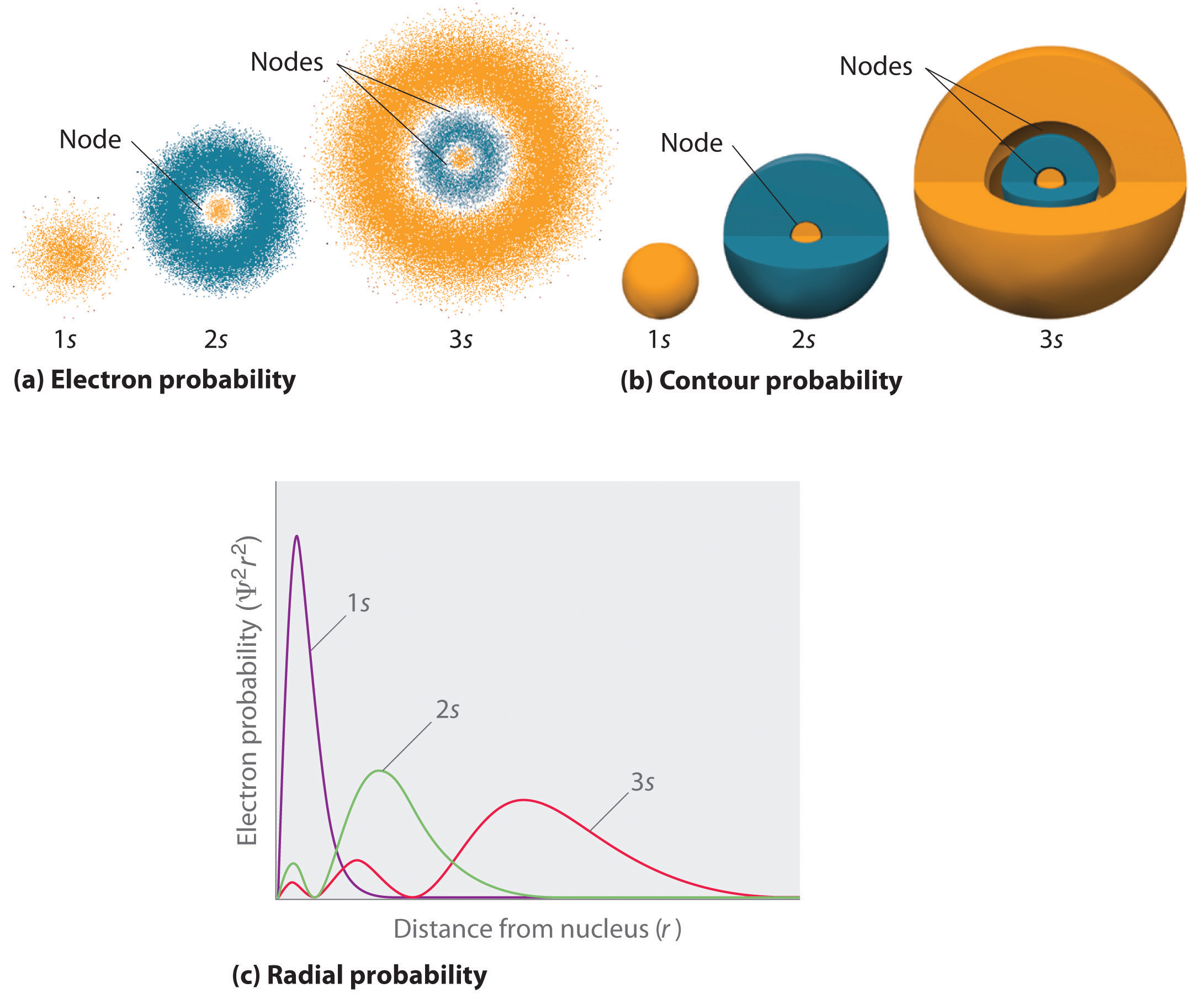
Kuvassa \(\PageIndex{2}\) verrataan vedyn 1s, 2s ja 3s -orbitaalien elektronien todennäköisyystiheyksiä\(r\). Huomaa, että kaikki kolme ovat pallosymmetrisiä. Elektronitodennäköisyystiheys ei kuitenkaan \(r\) 2s ja 3s -orbitaaleilla (eikä myöskään kaikilla muilla s-orbitaaleilla) laske tasaisesti \(r\):n kasvaessa. Sen sijaan säteittäisissä todennäköisyysdiagrammeissa (kuva \(\(\PageIndex{2c}\)) havaitaan sarja minimejä ja maksimeja. Minimit vastaavat pallomaisia solmuja (nollan elektronitodennäköisyyden alueita), jotka vuorottelevat nollasta poikkeavan elektronitodennäköisyyden pallomaisten alueiden kanssa. Näiden solmujen olemassaolo on seurausta aaltofunktion Ψ aaltovaiheen muutoksista.
s-orbitaalit (l=0)
S-orbitaaleille tapahtuu kolme asiaa n:n kasvaessa (kuva \(\(\PageIndex{2}\)):
- Neistä tulee suurempia, ja ne ulottuvat kauemmas \(r\) ytimestä.
- Neissä on enemmän solmuja. Tämä muistuttaa seisovaa aaltoa, jossa on merkittävän amplitudin alueita, jotka on erotettu solmuilla, eli pisteillä, joiden amplitudi on nolla.
- Tietyn atomin s-orbitaalien energia kasvaa myös korkeammaksi n:n kasvaessa, koskai\(r\) etäisyys ytimestä kasvaa.
Orbitaalit piirretään yleensä kolmiulotteisina pintoina, jotka sulkevat sisäänsä 90 % elektronitiheydestä, kuten \(r\) vedyn 1s, 2s ja 3s -orbitaaleista on esitetty kuvan \(\PageIndex{2}\) osassa (b). Vaikka tällaiset piirrokset osoittavat orbitaalien suhteelliset koot, niissä ei yleensä näy 2s- ja 3s-orbitaalien pallomaisia solmuja, koska pallomaiset solmut sijaitsevat 90 prosentin pinnan sisällä. Onneksi pallosolmujen sijainnit eivät ole tärkeitä\(r\) kemiallisessa sidoksessa.
p Orbitaalit (l=1)
Vain s-orbitaalit ovat pallosymmetrisiä. Kun l:n arvo kasvaa, orbitaalien lukumäärä\(r\) tietyssä alikuoressa kasvaa, ja orbitaalien muodot muuttuvat monimutkaisemmiksi. Koska 2p-alakuoren l = 1 ja ml:n kolme arvoa (-1, 0 ja +1), 2p-orbitaaleja on kolme.
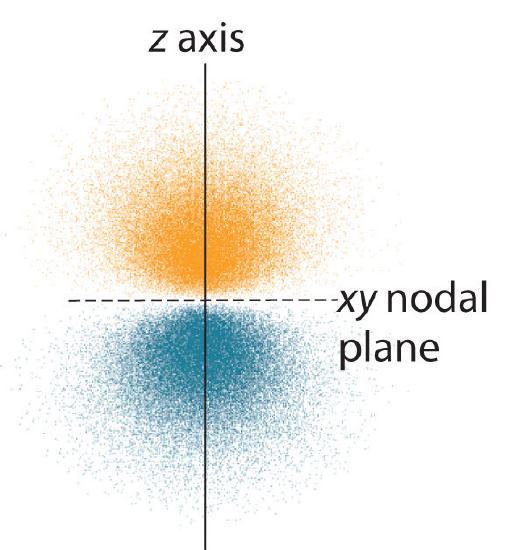
Elektronitodennäköisyysjakauma fo\(r\) yhdelle vedyn 2p-orbitaalista on esitetty kuvassa \(\PageIndex{3}\). Koska tällä orbitaalilla on kaksi z-akselin suuntaista elektronitiheyden lohkoa, joiden elektronitiheys on nolla xy-tasossa (eli xy-taso on solmutaso), se on \(2p_z\)-orbitaali. Kuten kuvassa \(\PageIndex{4}\) näkyy, muilla\(r\) kahdella 2p-orbitaalilla on identtinen muoto, mutta ne sijaitsevat x-akselin (\(2p_x\)) ja y-akselin (\(2p_y\)) suuntaisesti. Huomaa, että kullakin p-orbitaalilla on vain yksi solmutaso. Kussakin tapauksessa aaltofunktion fo\(r\) vaihe kullakin 2p-orbitaalilla on positiivinen fo\(r\) positiivisen akselin suuntainen lohko ja negatiivinen fo\(r\) negatiivisen akselin suuntainen lohko. On tärkeää korostaa, että nämä merkit vastaavat elektronin liikettä kuvaavan aaltofunktion vaihetta, eivät positiivisia o\(r\) negatiivisia varauksia.
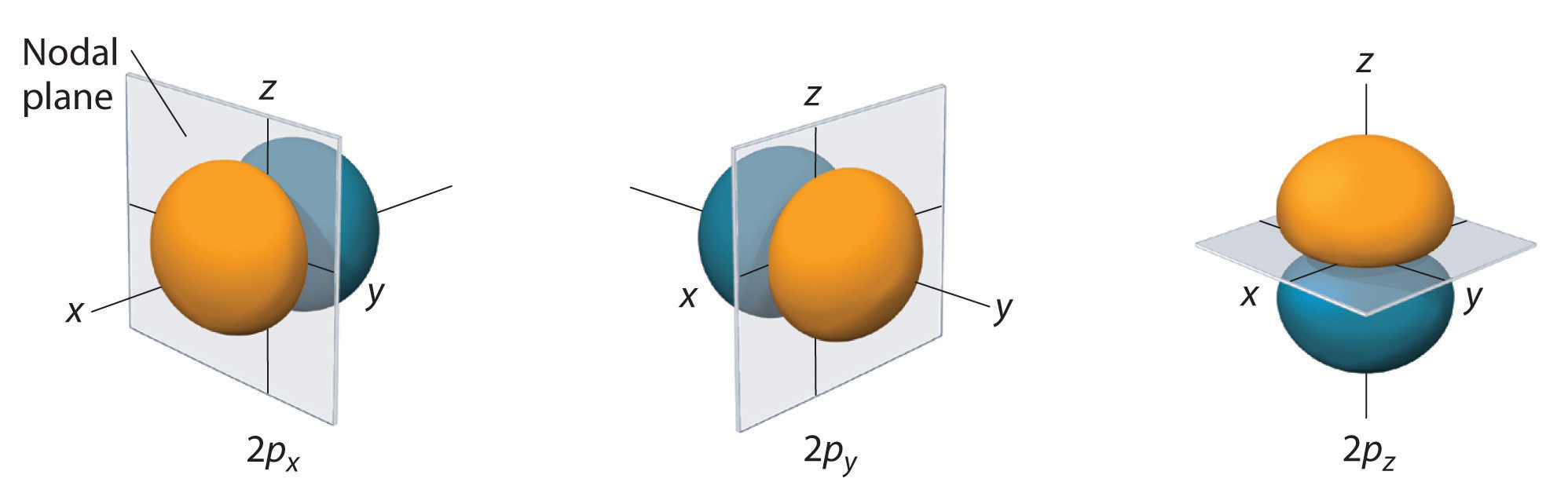
Kuvassa näkyvät pinnat sulkevat sisäänsä 90 % elektronin kokonaistodennäköisyydestä fo\(r\) 2px-, 2py- ja 2pz-orbitaalien 2px, 2py ja 2pz. Kukin orbitaali on suunnattu alaindeksillä merkittyä akselia pitkin, ja solmutaso, joka on kohtisuorassa \(r\) kyseiseen akseliin nähden, puolittaa jokaisen 2p-orbitaalin. Aaltofunktion vaihe on positiivinen (oranssi) alueella, jossa x, y, o\(r\) z on positiivinen, ja negatiivinen (sininen) alueella, jossa x, y, o\(r\) z on negatiivinen. Aivan kuten s-orbitaalien kohdalla, myös p-orbitaalien fo\(r\) koko ja monimutkaisuus kasvaa, kun pääkvanttilukube\(r\) n kasvaa. 3p-, 4p- ja korkeamman energian p-orbitaalien 90 %:n todennäköisyyspintojen muodot ovat kuitenkin olennaisesti samat kuin kuvassa \(\PageIndex{4}\).
d-orbitaalit (l=2)
Alakuorilla, joiden l = 2, on viisi d-orbitaalia; ensimmäinen pääkuori, jolla on d-alakuori, vastaa kuorta, jonka n = 3. Viiden d-orbitaalin ml-arvot ovat -2, -1, 0, +1 ja +2.
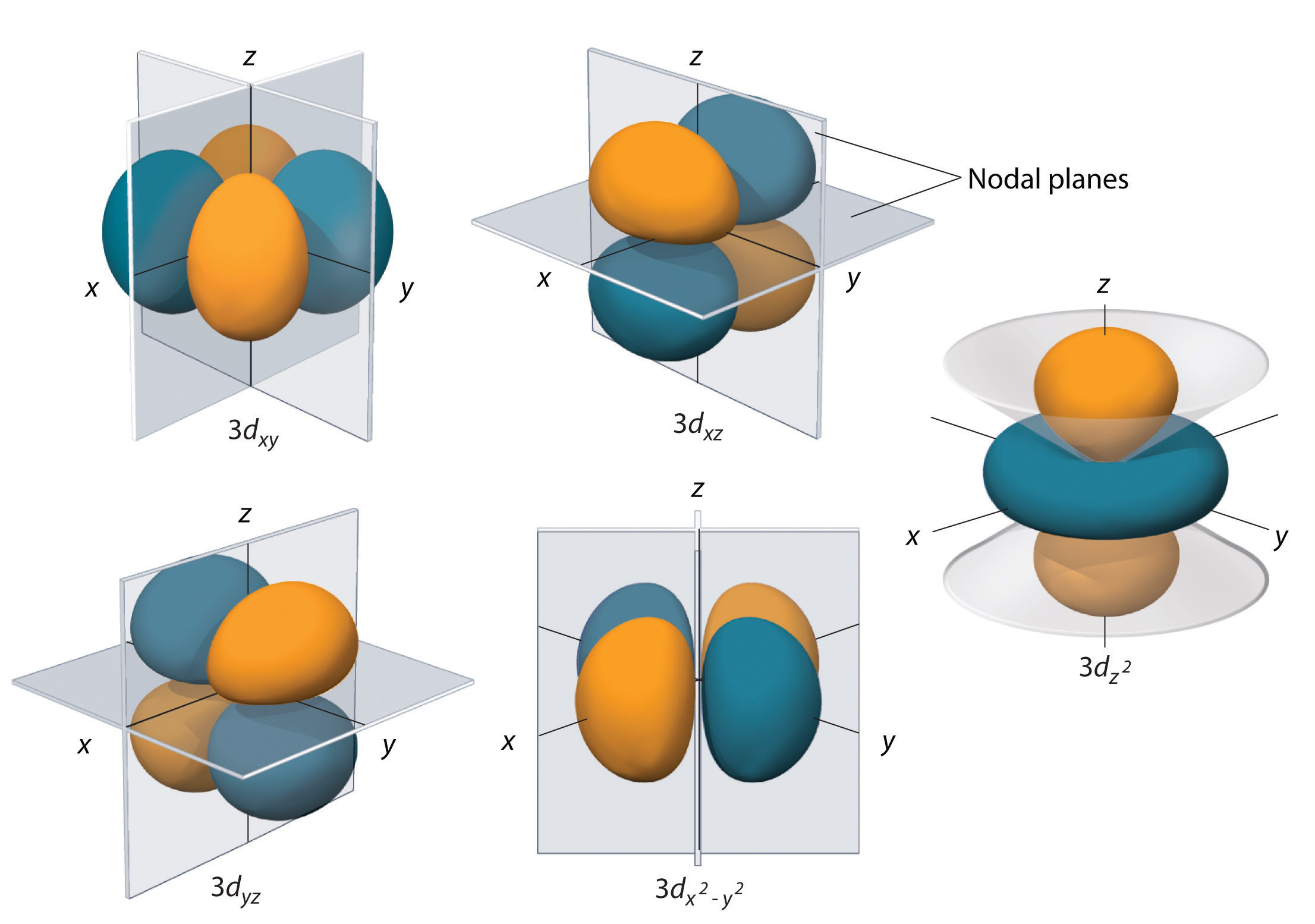
Kuvassa \(\(\PageIndex{5}\) esitetyillä vedyn 3d-orbitaaleilla on monimutkaisempi muoto kuin 2p-orbitaaleilla. Kaikissa viidessä 3d-orbitaalissa on kaksi solmupintaa, kun taas jokaisessa p-orbitaalissa on yksi fo\(r\) ja jokaisessa s-orbitaalissa nolla fo\(r\). Kolmessa d-orbitaalissa elektronitiheyden lohkot ovat suuntautuneet x- ja y-, x- ja z- sekä y- ja z-tasojen välille; näistä orbitaaleista käytetään nimityksiä \(3d_{xy}\), \)3d_{xz}\) ja \(3d_{yz}\) orbitaalit. Neljännen d-orbitaalin lohkot sijaitsevat x- ja y-akseleilla; tämä on \(3d_{x^2-y^2}\)-orbitaali. Viidennellä 3d-orbitaalilla, jota kutsutaan \(3d_{z^2}\)-orbitaaliksi, on ainutlaatuinen muoto: se näyttää \(2p_z\)-orbitaalilta, johon on yhdistetty xy-tasossa sijaitseva ylimääräinen elektronin todennäköisyyden donitsi. Erikoisesta \(r\)-muodostaan huolimatta \(3d_{z^2}\)-orbitaali vastaa matemaattisesti muuta \(r\) fou\(r\)-orbitaalia, ja sillä on sama energia. Toisin kuin p-orbitaaleissa, d-orbitaalien aaltofunktion vaihe on sama d-orbitaalien vastakkaisilla lohkopareilla. Kuten kuvassa \(\PageIndex{5}\) näkyy, aaltofunktion vaihe on positiivinen fo\(r\) \(dz^2\) orbitaalin kahdessa z-akselin suuntaisessa lohkossa, kun taas aaltofunktion vaihe on negatiivinen fo\(r\) elektronitiheyden donitsissa xy-tasossa. Kuten s- ja p-orbitaalien, myös d-orbitaalien koko kasvaa n:n kasvaessa, mutta kokonaismuodot pysyvät samanlaisina \(r\) kuin kuvassa \(\PageIndex{5}\).
f-orbitaalit (l=3)
Peruskuorilla, joiden n = 4, voi olla alikuoria, joiden l = 3 ja ml:n arvot ovat -3, -2, -1, 0, +1, +2, ja +3. Nämä alikuoret koostuvat seitsemästä f-orbitaalista. Jokaisella f-orbitaalilla on kolme solmupintaa, joteni\(r\) muodot ovat monimutkaisia. Koska f-orbitaalit eivät ole erityisen tärkeitä \(r\) ou\(r\) tarkoituksiin, emme käsittele niitä enempää, ja orbitaaleja, joilla on korkeammat l-arvot, ei käsitellä lainkaan.
Orbitaalienergiat
Vaikka olemme käsitelleet orbitaalien muotoja, olemme sanoneet vain vähän niideni\(r\) vertailevista energioista. Aloitamme keskustelun orbitaalien energioista tarkastelemalla atomeja o\(r\) ioneja, joilla on vain yksi elektroni (kuten H o\(r\) He+).
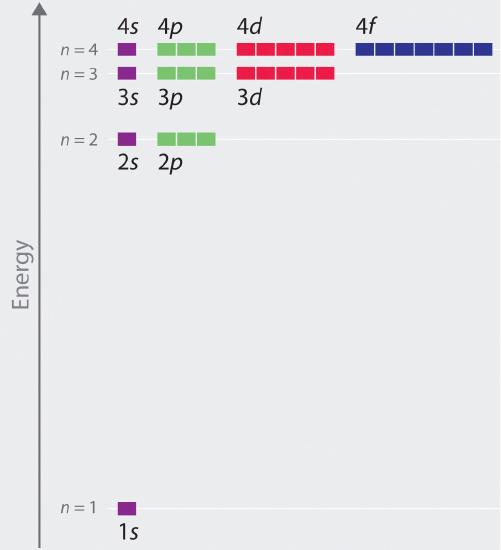
Kuvassa \(\(\PageIndex{6}\) on piirretty atomiorbitaalien suhteelliset energiat, kun n ≤ 4 vetyatomilla; huomaa, että orbitaalien energiat riippuvat vain pääkvanttiluvustabe\(r\) n. Näin ollen vedyn 2s- ja 2p-orbitaalien energiat ovat samat, 3s-, 3p- ja 3d-orbitaalien energiat ovat samat ja niin edelleen. Kvanttimekaniikka ennustaa, että vetyatomissa kaikki orbitaalit, joilla on sama n-arvo (esim. kolme 2p-orbitaalia), ovat degeneroituneita eli niillä on sama energia. Kvanttimekaniikan avulla vedylle \(r\) saadut orbitaalien energiat ovat täsmälleen samat kuin Bohin laskemat sallitut energiat. Toisin kuin Bohrin mallissa, jossa sallittiin vain yksi orbitaali fo\(r\) kutakin energiatasoa kohti, kvanttimekaniikka kuitenkin ennustaa, että n = 2 -pääkuoressa on neljä orbitaalia, joilla on erilaiset elektronitiheysjakaumat (yksi 2s ja kolme 2p-orbitaalia), n = 3 -pääkuoressa yhdeksän orbitaalia ja n = 4 -pääkuoressa 16 orbitaalia.Yksittäisten orbitaalien erilaiset l- ja ml-arvot tietyn pääkuoren sisällä eivät ole tärkeitä vetyatomin emissio- tai absorptiospektrien ymmärtämisessä useimmissa olosuhteissa, mutta ne selittävät pääviivojen jakautumisen, joka havaitaan, kun vetyatomit asetetaan magneettikenttään. Kuvasta \(\PageIndex{6}\) nähdään, että energiatasot muuttuvat läheisiksi\(r\) ja läheisiksi\(r\) yhdessä\(r\) n arvon kasvaessa, kuten on odotettavissa orbitaalien energioiden 1/n2-riippuvuuden vuoksi.
Orbitaalien energiat missä tahansa lajissa, jossa on vain yksi elektroni, voidaan laskea Bohrin yhtälön mino\(r\)-muunnoksella, joka voidaan laajentaa koskemaan muitakin\(r\)yhden elektronin lajeja ottamalla huomioon ytimen varauksen \(Z\) (protonien lukumäärä ytimessä):
\
Yleisesti ottaen sekä energia että säde pienenevät, kun ydin\(r\)-varaus kasvaa. Näin ollen stabiileimmat orbitaalit (ne, joilla on pienin energia) ovat ne, jotka ovat lähimpänä ydintä. Esimerkiksi vetyatomin perustilassa yksittäinen elektroni on 1s-orbitaalissa, kun taas ensimmäisessä kiihdytetyssä tilassa atomi on absorboinut energiaa ja elektroni on siirtynyt johonkin n = 2 -orbitaaleista. Ioneissa, joissa on vain yksi elektroni, tietyn orbitaalin energia riippuu vain n:stä, ja kaikki pääkuoren sisällä olevat alikuoret, kuten \(p_x\), \(p_y\) ja \(p_z\) orbitaalit, ovat degeneroituneita.
Yhteenveto
Kemiallisesti tärkeät atomiorbitaalityypit fou\(r\) vastaavat arvoja \(\ell = 0\), \(1\), \(2\) ja \(3\). Orbitaalit, joiden arvo on \(\ell = 0\), ovat s-orbitaaleja, ja ne ovat pallosymmetrisiä, ja suurin todennäköisyys elektronin löytymiselle on ytimessä. Kaikki orbitaalit, joiden arvot ovat \(n > 1\) ja \(ell = 0\), sisältävät yhden o\(r\) solmua enemmän. Orbitaalit, joiden arvo on \(\ell = 1\), ovat p-orbitaaleja, ja ne sisältävät solmutason, joka sisältää ytimen, jolloin syntyy käpylehmän muoto. Orbitaalit, joiden \(\ell = 2\) ovat d-orbitaaleja, ja niillä on monimutkaisempi muoto, jossa on vähintään kaksi solmupintaa. Orbitaalit, joissa on \(\ell = 3\), ovat f-orbitaaleja, jotka ovat vielä monimutkaisempia.
Koska elektronin keskimääräinen etäisyys ytimestä määrää elektronin energian, jokaiseen atomiorbitaaliin, jolla on tietty joukko kvanttilukuja, liittyy tietty \(r\) energia, orbitaalin energia.
\
Atomeissa o\(r\)ioneissa, joissa on vain yksi elektroni, kaikilla orbitaaleilla, joilla on sama \(n\)-arvo, on sama energia (ne ovat degeneroituneita), ja pääkuorien energiat kasvavat tasaisesti \(n\)-arvon kasvaessa. Atomin o\(r\)ionin, jonka elektroni(t) on (ovat) matalaenergisimmalla (matalaenergisimmilla) orbitaalilla (orbitaaleilla), sanotaan olevan perustilassaan, kun taas atomin o\(r\)ionin, jossa yksi o\(r\) elektroni(t) tai useampi elektroni on korkea-energisemmällä orbitaalilla (orbitaaleilla), sanotaan olevan virittyneessä tilassa.
Tekijät ja tekijät
-
Muokannut Joshua Halpern (Howardin yliopisto)