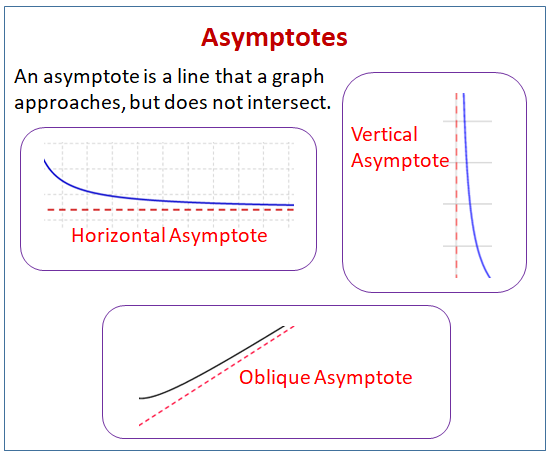
Asymptootti on viiva, jota kuvaaja lähestyy, mutta ei leikkaa.
Tällä oppitunnilla opettelemme löytämään rationaalifunktioiden pystysuorat asymptootit, vaakasuorat asymptootit ja vinot (vinot) asymptootit.
Seuraavat aiheet:
Lisäoppitunteja laskennasta

Oheisessa kaaviossa näkyvät erityyppiset asymptootit: vaakasuuntaiset asymptootit, pystysuuntaiset asymptootit ja vinot asymptootit. Vieritä sivua alaspäin saadaksesi lisää esimerkkejä ja ratkaisuja asymptoottien löytämiseen.

Miten määritetään pystysuora asymptootti?

Menetelmä 1: Käytä pystysuoran asymptootin määritelmää

Viivaa x = a sanotaan käyrän y = f(x) pystysuoraksi asymptoottiksi, jos vähintään yksi seuraavista väittämistä on tosi.

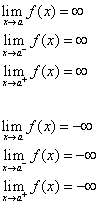
Menetelmä 2:

Rationaalifunktioille vertikaaliset asymptootit ovat pystysuoria viivoja, jotka vastaavat nimittäjän nollia.
Annetaan rationaalifunktio f(x)

Vaihe 1: Kirjoitetaan f(x) pelkistetyssä muodossa

Vaihe 2: Jos x – c on nimittäjässä tekijä, niin x = c on pystysuora asymptootti.

Esimerkki:

Etsitään pystysuorat asymptootit seuraavalle funktiolle:

Ratkaisu:

Menetelmä 1: Käytä vertikaalisen asymptootin määritelmää.

Jos x on lähellä 3 mutta suurempi kuin 3, niin nimittäjä x – 3 on pieni positiivinen luku ja 2x on lähellä 8. Eli on suuri positiivinen luku.

Intuitiivisesti nähdään, että

Vastaavasti, jos x on lähellä 3 mutta pienempi kuin 3, niin x – 3 on pieni negatiivinen luku ja 2x on lähellä 8. Siis on suuri negatiivinen luku.

Suora x = 3 on pystysuora asymptootti.

Menetelmä 2:

Vaihe 1: f(x) on jo pelkistetyssä muodossa.

Vaihe 2: Nimittäjä on x – 3, joten vertikaalinen asymptootti on kohdassa x = 3.

Rationaalifunktioiden vertikaalisten asymptoottien löytäminen

Mitä etsitään, jotta voidaan löytää rationaalifunktioiden vertikaaliset asymptootit.

• Näytä vaiheittaiset ratkaisut

Rationaalifunktioiden vertikaaliset asymptootit: Quick Way to Find Them

Esimerkki rationaalifunktioiden vertikaalisten asymptoottien löytämisestä.

• Näytä vaiheittaiset ratkaisut

Miten löydetään rationaalifunktioiden vertikaaliset asymptootit

• Näytä vaiheittaiset ratkaisut

Miten määritetään horisontaalinen asymptootti?

Menetelmä 1: Käytä vaakasuoran asymptotin määritelmää

Suoraa y = L sanotaan käyrän y = f(x) vaakasuoraksi asymptotiksi, jos joko

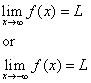
Menetelmä 2: Käytä vaakasuoran asymptotin määritelmää:

Rationaalifunktiolle f(x)

Jos x:n aste osoittajassa on pienempi kuin x:n aste nimittäjässä, niin y = 0 on vaakasuora asymptootti.

Jos x:n aste osoittajassa on yhtä suuri kuin x:n aste nimittäjässä, niin y = c, missä c saadaan jakamalla johtavat kertoimet.

Esimerkki:

Etsi funktion vaaka- ja pystyasymptootit.

Ratkaisu:

Menetelmä 1:

Jaa sekä osoittaja että nimittäjä luvulla x.

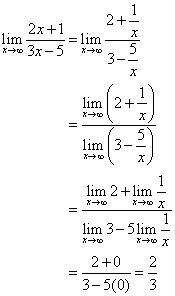
Viiva on vaakasuora asymptootti.

Menetelmä 2:

Luku x osoittajassa on yhtä suuri kuin luku x nimittäjässä.

Jakaen johtavat kertoimet saadaan

Viiva on vaakasuora asymptootti.

Lyhytleikkaus rationaalifunktioiden vaakasuuntaisten asymptoottien löytämiseen

Pari niksiä, joiden avulla rationaalifunktioiden vaakasuuntaisten asymptoottien löytäminen on erittäin helppoa

• Näytä vaiheittaiset ratkaisut

Tämässä videossa annetaan peruskatsaus vaakasuuntaisista asymptoteista. Määritämme, onko annetuilla rationaalifunktioilla vaakasuoria asymptootteja ja mitä ne ovat.

• Näytä vaiheittaiset ratkaisut

Tällä videolla tutustutaan tarkemmin vaakasuoria asymptootteja koskeviin sääntöihin.

• Näytä vaiheittaiset ratkaisut

Vino asymptootti eli vinousasymptootti

Joillakin rationaalifunktioiden käyrästöillä on asymptootteja, jotka ovat vinoja eli eivät ole vaakasuoria eivätkä pystysuoria.

Jos , niin suoraa y = mx + b kutsutaan vinoksi tai vinoksi asymptotiksi, koska käyrän y = f(x) ja suoran y = mx + b pystysuorat etäisyydet lähestyvät 0:aa.

Rationaalifunktioille vinot asymptotit esiintyvät silloin, kun osoittajan asteluku on yhtä suurempi kuin nimittäjän asteluku. Tällöin vinon asymptootin yhtälö voidaan löytää pitkällä jaolla.

Esimerkki:

Löydä funktion

asymptootit

Ratkaisu:

Sen vuoksi, että nimittäjä x2 + 1 ei ole koskaan 0, ei ole pystysuoraa asymptoottia.

Sen vuoksi, että osoittajan x:n aste on suurempi kuin nimittäjän x:n aste, ei ole vaakasuoraa asymptoottia.

Sen vuoksi, että osoittajan x:n aste on yhtä suurempi kuin nimittäjän x:n aste, voimme käyttää pitkää jakoa saadaksemme vinon asymptotin.

Suora y = x on siis vino asymptootti.

Rationaalifunktioiden vinojen asymptoottien löytäminen

Tässä videossa kuvataan, milloin rationaalifunktiolla on vino asymptootti, kerrotaan lyhyesti, mikä on vino asymptootti, ja tehdään kaksi esimerkkiä.

• Näytä vaiheittaiset ratkaisut

Rationaalifunktion asymptoottien löytäminen (pystysuora, vaakasuora ja vino/viisto)

Tässä videossa näytetään, miten rationaalifunktion pystysuora asymptootti ja vino/viisto asymptootti löydetään.

• Näytä vaiheittaiset ratkaisut

Rationaalifunktion kaikkien asymptoottien löytäminen (pystysuora, vaakasuora ja vino/kalteva)

Tässä tarkastelemme funktiota ja löydämme pystysuoran asymptootin ja päätämme myös, että vaakasuoria asymptootteja ei ole, mutta vino asymptootti on olemassa. Tämän jälkeen käytämme pitkää jakoa löytääksemme vinon asymptotin.

• Näytä vaiheittaiset ratkaisut

Kokeile alla olevaa ilmaista Mathwayn laskinta ja ongelmanratkaisijaa harjoitellaksesi erilaisia matemaattisia aiheita. Kokeile annettuja esimerkkejä tai kirjoita oma ongelmasi ja tarkista vastauksesi vaiheittaisten selitysten avulla.