
Galileota pidetään usein modernin tieteen isänä. Hän oli se, joka kokosi kokeen, teorian ja matematiikan periaatteet yhteen yhtenäiseksi kehykseksi. Luultavasti enemmän kuin kukaan muu Galilei oli vastuussa modernin tieteen kehittämisestä.
Se kertoo, että Galilei pudotti Pisan kaltevan tornin päältä kaksi erimassaista, mutta samaa materiaalia olevaa teräspalloa ja ne laskeutuivat samaan aikaan. Merkittävää tässä kokeessa on se, että hän aloitti uuden tieteen tekemisen menetelmän, jossa tehdään koe hypoteesin testaamiseksi. Hän osoitti, että meidän on tehtävä muutakin kuin vain ajateltava, että jokin on totta, vaan meidän on myös todistettava se.”

Galileo löysi mielenkiintoisen paradoksin ollessaan Pisan yliopiston matematiikan laitoksen johtajana.
Määritelmä: Paradoksi, joka tunnetaan myös nimellä antinomia, on loogisesti itselleen ristiriitainen väite tai väite, joka on vastoin odotuksia. (Wikipedia). (kreik. ”para” = tuonpuoleinen, ”doxa” = uskomus)
Galileon paradoksissa oli kyse sen selvittämisestä, ovatko kaksi äärettömiä objekteja sisältävää joukkoa toisiaan vastaavia. Olkoon esimerkiksi P positiivisten kokonaislukujen joukko, jossa P= {0,1,2,3,…} ja E parillisten lukujen joukko, jossa E = {0,2,4,6,…}. Galilei väitti, että näiden kahden joukon koot tulevat olemaan samat, koska voimme parittaa jokaisen positiivisen kokonaisluvun joukosta P parillisilla luvuilla joukosta E.

Miten näiden kahden joukon koot tulevat olemaan samat silloin, kun joukossa E esiintyy ”pienempi” luku? Tätä kutsuttiin Galileon paradoksiksi, ja se käynnisti uuden keskustelun äärettömyyden käsitteestä.
Galileon jälkeen hänen oppilaansa Evangelista Torricelli nousi Pisan yliopiston matematiikan laitoksen johtajaksi. Olet ehkä kuullut hänestä hänen ilmakehän painetta koskevien töidensä ja barometrin keksimisen vuoksi. Koska Toricelli on kiinnostunut myös matematiikasta, hän kysyy:
Onko mahdollista, että esineellä on äärellinen tilavuus ja ääretön pinta? Ensinnäkin sellainen tuntuu useimmille meistä epätodennäköiseltä. Matematiikka kuitenkin kertoo meille, että sellainen voisi tapahtua. Torricelli vastasi itse kysymykseensä ja löysi Toricellin trumpetin, jonka pinta-ala on ääretön, mutta tilavuus äärellinen. Hänen löytönsä nähtiin ”uskomattomana” paradoksina.
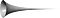
Matematiikan filosofiassa on muuten olennainen sääntö; Minkä aikakauden filosofian tai matematiikan kanssa on tekemisissä, se liittyy kyseisen alueen historiaan, kulttuuriin ja uskontoon. Siksi Toricellin trumpettia kutsutaan myös Gabrielin torveksi. Tässä viitataan Raamattuun, koska kristityt uskovat, että enkeli Gabriel puhaltaa torveen tuomiopäivänä.
Miten Toricellin trumpetti siis muodostuu? Me kaikki tiedämme, miten kuvaaja y=x muodostetaan. Jos sen sijaan kuvaajaksi otetaan yhtälö y=1/x, jossa x on suurempi tai yhtä suuri kuin 1, kuvaaja on seuraavanlainen:
Kun otamme kuvaajan y=1/x ja käännämme sitä x-akselin ympäri, näemme Toricellin trumpetin.

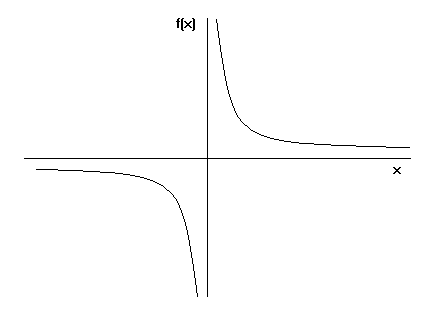
Onneksi käsissämme on matemaattiset kaavat, joilla voimme laskea Toricellin trumpetin pinta-alan ja tilavuuden. Kun käytämme alla olevaa integrointikaavaa trumpetin tilavuudelle, saamme äärellisen määrän.
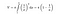
Kun taas sovellamme integraatiokaavaa trumpetin pinta-alalle, tällä kertaa trumpetin pinta-alasta tulee ääretön. Eikö tämä tulos olekin mielenkiintoinen?
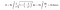
Koska Toricellin trumpetin tilavuus on äärellinen, voimme täyttää sen äärellisellä määrällä maalia. Oletetaan esimerkiksi, että sen tilavuus on 100 litraa. Menen Home Depotiin ja ostan 100 litraa maalia ja täytän sen. Mielenkiintoiseksi tämän tekee kuitenkin se, että olen maalannut äärettömän pinnan tuolla 100 litralla maalia. Nykyään useimmat ihmiset kutsuvat tätä paradoksia ”maalarin paradoksiksi.”
Houston, meillä on ongelma! Tilanne, joka on käytännössä mahdoton, muuttuu matematiikassa mahdolliseksi. Miten siis Torricellin trumpetti voi olla todellinen? Tai miten voimme täsmällisesti sovittaa yhteen kaikki joukkojen elementit, kun yksi joukoista on Galileon esimerkissä toisen osajoukko?
Syy kaikkiin näihin ristiriitoihin on se, että äärettömyyden käsite ei ole samanlainen kuin muut tuntemamme käsitteet, ja se hämmentää monia ihmisiä. Galileo sanoo paradoksilleen,
”Kyllä, ystäväni, ääretön on olemassa. Sitä on turha vastustaa. Joukot, joita käsittelen, ovat esimerkkejä suljetuista joukoista, joihin liittyy äärettömyys. Ne alkavat pisteestä ja jatkuvat äärettömyyteen, ja silti ne ovat edelleen joukko. Äärettömyyttä koskevien kommenttieni ja käsitteitteni on kuitenkin oltava erilaisia kuin ne, joita käyttäisin äärellisten suureiden kohdalla. Jos kyse on äärellisistä suureista, voidaan sanoa, että 3 kiloa on vähemmän kuin 5 kiloa tai 32 metriä on pidempi kuin 7 metriä. Mutta kun on kyse äärettömyydestä, ei voi sanoa, että tämä äärettömyys on suurempi, pienempi tai yhtä suuri kuin tuo.”
Tämä oli Galileon ratkaisu 1600-luvulla.
Epäonnekseen Galileon ratkaisu oli aloittanut uuden keskustelun äärettömyydestä. Matemaatikot ja filosofit eivät päässeet yksimielisyyteen täsmällisestä vastauksesta, kunnes Cantor kertoi ”joukko-opistaan”, jota oppilaat oppivat nykyään peruskoulussa.
Voidaan ajoittain historioida äärettömyyden idean kehitystä. Se syntyi ensimmäisen kerran Eleatikoissa, joka oli esisokraattinen filosofinen koulukunta, jonka Parmenides perusti viidennen vuosisadan alussa eaa. antiikin Elean kaupungissa. Tähän koulukuntaan kuului kolme suurta filosofia, kuten Zenon, Ksenofanes ja Parmenides. Tässä koulukunnassa hyväksytty filosofia oli, että olemassaolo oli singulaarinen, eikä moninaisuutta ollut olemassa. Zenon oli Eleatikoilla kuuluisa äärettömyyttä koskevista paradokseistaan. Myöhemmin 300-luvulla eKr, Aristoteles nousi esiin ja ehdotti Zenonin paradoksin selittämiseksi käsiteparia, jotka olivat potentiaalinen äärettömyys ja todellinen äärettömyys.
Potentiaalinen äärettömyys on lukujoukko tai joukko ”asioita”, joka jatkuu päättymättä, jatkuu tai toistuu yhä uudelleen ilman tunnistettavaa päätepistettä.
Todellisessa äärettömyydessä on kyse päättymättömistä joukoista tai ”asioista” tilassa, jolla on alku ja loppu; se on sarja, joka on teknisesti ”päättynyt”, mutta joka koostuu äärettömästä määrästä jäseniä.
Aristoteles uskoi, että varsinaista äärettömyyttä ei ole olemassa. Tämä Aristoteleen ajatus hallitsi filosofiaa 1600-luvulle asti. Sitten filosofit kuten Cusa ja Bruno väittivät, että varsinainen äärettömyys on olemassa, mutta emme voi ymmärtää sitä. Cusan ja Brunon jälkeen aiheeseen liittyi suuri ajattelija Spinoza.
Spinoza sanoi, että voimme ymmärtää äärettömyyden käsitteen ja asettaa ne suuruusjärjestykseen. Hän kuitenkin totesi myös, että hän ei pystynyt laskemaan niitä. Hän pystyi esimerkiksi laskemaan 3:n ja 5:n yhteen, mutta hän ei pystynyt laskemaan yhtä ääretöntä toiseen.
Viimein noiden väittelyjen päätteeksi paikalle ilmaantui komea mies, Georg Cantor, joka löysi joukko-opin, joka on edelleen matematiikan perusta. Hän asetti äärettömyyskeskusteluille lopullisen pisteen joukko-opillaan.
Hän osoitti meille, että ääretön joukko olisi suurempi tai pienempi kuin toinen ääretön joukko. Lisäksi Cantor väitti, että voimme lisätä ja kertoa äärettömiä joukkoja. Siihen asti ihmiset olivat noudattaneet Aristoteleen ajatuksia äärettömyydestä. Aristoteleen mukaan jos kertoisimme luvun 3 äärettömyydellä, siitä tulisi taas ääretön. Äärettömyys nielisi kaiken. Tämän perusteella hän väitti, että olisi olemassa vain potentiaalinen äärettömyys, ei todellista äärettömyyttä.
Cantor kuitenkin todisti meille joukko-opin avulla Aristoteleen ajatuksen vastakohdan. Jos lisäämme äärettömään joukkoon yhden, se ei ole enää sama joukko. Hän yritti verrata äärettömyyksiä. Cantor esimerkiksi todisti, että kaikkien funktioiden joukko (0,1)→ℕ on laskettavissa. Näin hän määritteli yksikäsitteisen ja onto-funktion intervallista (0,1) luonnollisiin lukuihin.
Muulla sanoen hän todisti, että kaikki luonnolliset luvut mahtuvat välille 0 ja 1, koska välille 0-1 oli äärettömiä rationaalilukuja, ja nämä äärettömyydet voidaan parittaa. Sitten hän teki jotain vielä vaarallisempaa kuin kahden yhtä suuren äärettömyyden löytäminen. Hän vertasi reaalilukujen äärettömyyttä luonnollisten lukujen äärettömyyteen ja totesi, että reaalilukujen äärettömyys on suurempi kuin toinen. Hän jopa katsoi todistustaan ja sanoi ystävälleen Dedekindille: ”Näen sen, mutta edes minä en voi uskoa sitä …”.
Cantor oli myös matemaatikko, jolla oli hyvin vakavia filosofisia ja uskonnollisia huolia. Joukkoteoriaa kehittäessään hän sanoi: ”Jumala saneli minulle joukko-opin.”
Joukkoteoriaa kehitettäessä sitä ei hyväksytty laajalti. Yritykset eivät edes palkanneet Cantoria mihinkään työhön. Matemaatikko Henri Poincaré sanoi kerran: ”Tämän Cantorin ajatukset ovat paha tauti, joka tarttuu matematiikan kaulukseen. Ja matematiikka hoitaa hänet jonain päivänä”. Cantor joutui joksikin aikaa mielisairaalaan ja kuoli siellä. Mutta nykyään pidämme häntä nerona.
Cantor oli yksinäinen mies äärettömyyden äärellä. Hän siteerasi Raamattua transfiniittisiä lukuja käsittelevän artikkelinsa alussa: ”Kaikki, mikä on kätketty, tulee päivänvaloon.”