Seuraavana on näkemykseni joistakin matematiikkaongelmista, jotka liittyvät oletettavasti ”common core -matematiikkaan” tai ”uuteen matematiikkaan” ja jotka ovat levinneet internetissä. Mielestäni ne osoittavat meille CCS:n vääränlaista toteutusta.
Pitäkää mielessä, että kaikkea, mitä näette matematiikan kirjoissa tai internetissä, ei ole tehty oikein CCS:n pohjalta. Joissakin näkemissänne esimerkeissä näyttää siltä, että ihmiset hylkäävät maalaisjärjen tehdessään matemaattisia ongelmia Common Core -standardien mukaisesti!
En ole yllättynyt siitä, että toteutus on päätynyt joissakin paikoissa ”mönkään”. CCS on useimmille opettajille niin suuri muutos, että he tarvitsevat paljon tukea ja uudelleenkoulutusta ennen kuin he joutuvat opettamaan niiden mukaan.
Olen aina ollut sitä mieltä, että AVAIN ongelma matematiikan opetuksessa peruskoulun alaluokilla julkisissa kouluissa on se, että monet peruskoulun opettajat eivät ymmärrä matematiikkaa riittävästi pystyäkseen opettamaan sitä oikein edes alaluokilla. Monet heistä eivät esimerkiksi ymmärrä opettamiensa algoritmien käsitteitä, miksi ja mistä. Se ei ole heidän vikansa – ongelma juontaa juurensa siihen, mitä heille on opetettu opettajankoulutuksessa ja heidän omassa koulunkäynnissään.
Jopa itse standardeja koskeva asiakirja on paikoin hieman vaikeaselkoinen. Sen lukeminen vaatii jonkin verran ajattelua. Toivoisin, että joku tuottaisi vihkosen, jossa standardit selitettäisiin yksinkertaisella kielellä ja lukuisilla esimerkeillä.
Huonoja esimerkkejä ”common coresta” tai ”uudesta matematiikasta”
Esimerkki 1
Viime aikoina näin Facebookissa kuvan vähennyslaskustrategioista, jossa väitettiin, että se oli 1. luokan matematiikan kirjasta ja että se oli ”Common Core -matematiikkaa”.”
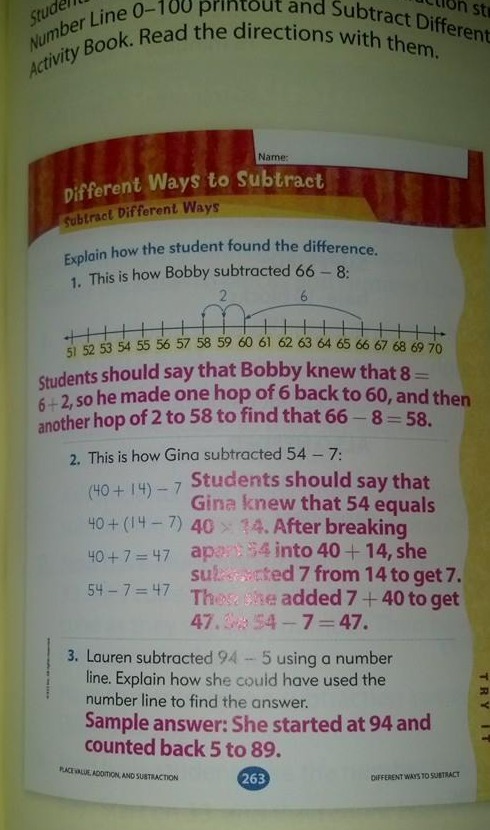
Minusta menetelmä 2 on aivan liian vaikea 1. luokalle, ja jättäisin jopa menetelmän 1 2. luokalle.”
Vaikka tuo kirja ei näytä edes olevan Common Core -standardien mukainen. 1. luokan standardit eivät yksinkertaisesti sisällä tuollaisia vähennyslaskutehtäviä!”
Tämä löytyy standardeista:
Lisää ja vähennä 20:n sisällä.
1.OA.5.
Suhteuttaa laskemista yhteen- ja vähennyslaskuun (esim. laskemalla 2:een lisätään 2).
1.OA.6.
Lisätä ja vähennä 20:n sisällä osoittaen sujuvuutta yhteen- ja vähennyslaskussa 10:n sisällä. Käyttää strategioita, kuten yhteenlasku, kymmenen muodostaminen (esim. 8 + 6 = 8 + 2 + 4 = 10 + 4 = 14), kymmeneen johtavan luvun purkaminen (esim. 13 – 4 = 13 – 3 – 1 = 10 – 1 = 9), yhteen- ja vähennyslaskujen välisen suhteen käyttäminen (esim. kun tietää, että 8 + 4 = 12, tietää, että 12 – 8 = 4) ja vastaavien, mutta helpompien tai tunnettujen summien muodostaminen (esim, lisäämällä 6 +7 luomalla tunnettu ekvivalentti 6 + 6 + 1 = 12 + 1 = 13).
Lukukirjan esimerkki näyttää haluavan käsitellä edellä mainittua 1.OA.6 kohtaa, mutta se koskee selvästi yhteen- ja vähennyslaskuja 20:n rajoissa, ei isompien lukujen kanssa.
Myöhemmin 1. luokan standardeissa näemme kaksi standardia, jotka liittyvät kaksinumeroisten lukujen (100:n rajoissa tapahtuvaan) vähentämiseen:
1.NBT.5.
Kaksinumeroisen luvun avulla etsitään mentaalisesti 10 lukua enemmän tai 10 lukua vähemmän ilman laskemista; selitä käytetyt perustelut.
1.NBT.6.
Vähennä 10:n kertaluvut välillä 10-90 10:n kertaluvuista välillä 10-90 (positiiviset tai nollaerot) käyttäen konkreettisia malleja tai piirroksia ja strategioita, jotka perustuvat paikka-arvoon, operaatioiden ominaisuuksiin ja/tai yhteenlaskun ja vähennyslaskun väliseen suhteeseen; liitä strategia kirjalliseen menetelmään ja selitä käytetyt perustelut.
Marian huomautus: tämä tarkoittaa vähennyslaskuja, kuten 34 – 20 tai 89 – 60.
mutta kumpikaan näistä ei sisällä vähennyslaskuja, kuten 54 – 7 tai 82 – 6. Ne ovat 2. luokalla:
2.NBT.5.
Sujuva yhteen- ja vähennyslasku sadan sisällä käyttäen strategioita, jotka perustuvat paikka-arvoon, operaatioiden ominaisuuksiin ja/tai yhteen- ja vähennyslaskun väliseen suhteeseen.
Huomaa, että 2. luokan standardi ei määrittele, MITEN vähennetään (käytetäänkö mentaalimatematiikan strategioita vai kirjoitetaanko numeroita toistensa alle ja lainataan/ryhmitelläänkö).
Esimerkki 2
Hughton Miffliniltä, oletettavasti:
Juanita haluaa antaa pussillisia tarroja ystävilleen. Hän haluaa antaa jokaiselle ystävälle saman määrän tarroja. Hän ei ole varma, tarvitseeko hän 4 vai 6 pussia tarroja. Kuinka monta tarraa hän voisi ostaa, jotta tarroja ei jäisi yli?
Tarraongelma liittyy pienimmän yhteisen kertaluvun (LCM) käsitteeseen. (Vastaus on, että hänen pitäisi ostaa 12, 24, 36 tai mikä tahansa muu 12 tarran kerrannainen, koska silloin hän voi jakaa ne joko 4 pussiin tai 6 pussiin.)
Totta kai, ongelma on ERITTÄIN epäselvä ja huonosti muotoiltu. Veikkaan, että se vihkonen, jossa tämä esiintyy, on yksinkertaisesti muokkaamaton. Se ei ole itse standardien vika. Olen samaa mieltä Bart Goddardin kanssa Math Forumissa. Tämä on oire sokeasta kiireestä tuottaa ”tosielämän” tarinaongelmia, jotka ovat lopulta järjettömiä.
PDF-dokumentista, jossa se esiintyy, päättelen ongelman olevan neljännelle luokalle, koska kaikki muut vihkon sanaongelmat vastaavat neljännen luokan standardeja (tekijät, alkuluvut). Mutta CCS:ssä ei edes mainita pienintä yhteistä monikertaa 4. luokan standardeissa (se on 6. luokassa)!!! Jotain meni todella pieleen tuon sanatehtävän kanssa.
Esimerkki 3

Jälleen kerran, oletettavasti Houghton Miffliniltä 1. luokalle. Tämä vastaa jo edellä siteeraamaani standardia:
Add and subtract within 20.
1.OA.6.
Add and subtract within 20, demonstrating fluency for addition andsubtraction within 10. Käyttää strategioita, kuten jatkolaskua, kymmenen muodostamista (esim. 8 + 6 = 8 + 2 + 4 = 10 + 4 = 14), kymmeneen johtavan luvun purkamista (esim. 13 – 4 = 13 – 3 – 1 = 10 – 1 = 9), yhteen- ja vähennyslaskun välisen suhteen käyttämistä (esim, kun tiedetään, että 8 + 4 = 12, tiedetään, että 12 – 8 = 4); ja ekvivalenttien, mutta helpompien tai tunnettujen summien luominen (esim. lisäämällä 6 +7 luomalla tunnettu ekvivalentti 6 + 6 + 1 = 12 + 1 = 13).
Aluksi: ”kymppien tekemisen” strategia liittyy LISÄÄMISEEN, ei vähennykseen. Vähennyslaskussa sitä kutsutaan ”kymmeneen johtavan luvun hajottamiseksi”. Ohjeissa pitäisi siis kysyä: ”Mikä osoittaa tavan purkaa kymmeneen johtava luku?”. Minusta on täyttä hölynpölyä vaatia ensimmäisen luokan oppilaita tuntemaan tällaista terminologiaa.
Mutta tässä on toinenkin ongelma. Jos todella luet kaikki standardit, huomaat, että useissa muissa paikoissa oppilaita pyydetään selittämään käytetyt perustelut tai liittämään tietty visuaalinen menetelmä strategiaan, mutta EI tässä standardissa!
Minä näen tämän standardin niin, että opettajien pitäisi OPETTAA mainitut eri strategiat ja sitten antaa oppilaille yksinkertaisia yhteenlasku- ja vähennyslaskutehtäviä 20:n rajoissa, kuten 15 – 8 ja 10 – 6. En näe, että tässä standardissa vaaditaan oppilaita tunnistamaan, vastaako tietty visuaalinen malli tiettyä strategiaa.
Jälleen kerran näyttää siltä, että kirjoittaja hylkää maalaisjärjen… eikä oikeasti ymmärrä standardeja.
Esimerkki 4
Alla oleva esimerkki on erittäin huonosti muotoiltu, mutta sen takana oleva KONSEPTI on erittäin hyvä, ja se löytyy myös Math Mammothista. Voin siis päätellä, mitä he haluavat.

Näet viisi neliötä. Väritä osa siniseksi ja loput punaiseksi. Se on selvä.
Väritä sitten ”numerosidoksen” ruudut samalla tavalla. Numerosidos menee noihin kolmeen ympyrään. Lapsi, joka on ollut läsnä oppitunnilla, jossa opettaja opettaa numerosidoksia, tietää toivottavasti, mitä se tarkoittaa. Se on sama käsite kuin faktaperhe… Ylin luku on summa tai kokonaisluku (5), ja alempiin ympyröihin menevät luvut vastaavat sitä, kuinka monta väritit siniseksi ja kuinka monta punaiseksi, tässä tapauksessa 1 ja 4.
Silloin luulen, että piilotetut parit ovat myös ne 1 ja 4. Näytä 1 ja 4 sormia aikuiselle. Väritä lopuksi 1 ja 4 sormet kuvaan (eikä omia sormia kuten kuulostaa).
Minusta tuo sormia koskeva kohta on superflous ja sekava. Numerosidosten käsite on kuitenkin paljon vanhempi kuin CCS. Numerosidoksia ei itse asiassa mainita CCS:ssä, vaikka ne liittyvätkin tähän standardiin:
1.OA.4
Ymmärtää vähennyslasku tuntematon-lisäysongelmana. Esimerkiksi vähennä 10 – 8 etsimällä luku, joka on 10, kun se lisätään 8:aan.
ja tämän
1.OA.6.
Lisää ja vähennä 20:n sisällä, osoittaen sujuvuutta yhteenlaskussa ja vähennyslaskussa 10:n sisällä.
1.OA.6.
En tiedä, miksi tuo number bond -tehtävälehtinen mainitaan esimerkkinä yhteisten perusopetussääntöjen mukaisesta matematiikasta. Se olisi paljon paremmin otsikoitu esimerkkinä huonosti muotoillusta matemaattisesta työlehdestä, joka VOISI jopa olla peräisin ajalta ennen Common Corea (ja jota vain käytetään uudelleen tässä nimenomaisessa opetussuunnitelmassa)… koska kuten sanoin, numerobondeja EI mainita CCS:ssä.Mitä Common Core -matematiikkastandardit eivät ole
- Neuvot eivät ole ”uutta matematiikkaa”. Verrattuna moniin 2000-luvulla käytettyihin matematiikan opetussuunnitelmiin, jotka painottivat ei-perinteisiä algoritmeja, CCS on selkeä siirtyminen kohti perinteisiä algoritmeja ja ulkoa opettelua. Tutustu näihin erityisiin standardeihin:
2.OA.2
Lisää ja vähennä sujuvasti 20:n sisällä käyttäen mentaalistrategioita. Osaa 2. luokan loppuun mennessä ulkoa kaikki kahden yksinumeroisen luvun summat.
Marian huomautus: Nämä ovat yhteenlaskun perusfaktoja, kuten 7 + 7 tai 5 + 4.3.OA.7
Kertoa ja jakaa sujuvasti 100:n sisällä käyttäen strategioita, kuten kerto- ja jakolaskun välisiä suhteita (esim. kun tietää, että 8 × 5 = 40, tietää, että 40 ÷ 5 = 8) tai operaatioiden ominaisuuksia. Kolmannen luokan loppuun mennessä osaa ulkoa kaikki kahden yksinumeroisen luvun tulot.
Marian huomautus: tämä tarkoittaa kertotauluja ja perusjakotietoja.4.NBT.4
Suorittaa sujuvasti yhteen- ja vähennyslaskuja moninumeroisista kokonaisluvuista käyttäen standardialgoritmia.5.NBT.5
Kerrata sujuvasti moninumeroisia kokonaislukuja käyttäen standardialgoritmia.
Marian huomautus: tämä ei tarkoita sitä, että oppilaat kertovat moninumeroisia kokonaislukuja vasta viidennellä luokalla, vaan sitä opiskellaan myös 3. ja 4. luokalla.- Standardit eivät määrää opettajille ja oppilaille outoja strategioita tai visuaalisia malleja. Monet standardit jättävät sen opettajien ja oppilaiden tehtäväksi. Esimerkiksi:
2.NBT.5
Sujuvaa yhteen- ja vähennyslasku 100:n sisällä käyttäen strategioita, jotka perustuvat paikka-arvoon, operaatioiden ominaisuuksiin ja/tai yhteen- ja vähennyslaskun väliseen suhteeseen.Huomaa ”ja/tai” yllä olevassa lauseessa. Tämä tarkoittaa, että opettajia ja oppilaita EI ole rajoitettu käyttämään mitään tiettyä strategiaa eikä kehotettu käyttämään useita strategioita. Perinteinen ”laina-algoritmi” on paikka-arvoon perustuva strategia, joten se sisältyy juuri tähän kohtaan 2.NBT.5.
2.NBT.9
Erittele, miksi yhteen- ja vähennyslaskustrategiat toimivat paikka-arvon ja operaatioiden ominaisuuksien avulla. Selityksiä voidaan tukea piirroksilla tai esineillä.Se sanoo ”voidaan tukea piirroksilla”, mutta se ei pakota siihen eikä rajoita käyttämään tiettyä visuaalista mallia tai piirrostyyppiä.
3.OA.3.
Käyttää kerto- ja jakolaskuja 100:n sisällä ratkaistakseen sanaongelmia tilanteissa, joihin liittyy yhtäsuuria ryhmiä, joukkoja ja mittaussuureita,esim. käyttämällä piirroksia ja yhtälöitä, joissa on tuntemattoman luvun symboli ongelman esittämiseksi.Opiskelijan ei PITÄÄ käyttää piirrosta. Se vain mainitaan mahdollisuutena.
4.NBT.5
Kertoo enintään nelinumeroisen kokonaisluvun yksinumeroisella kokonaisluvulla ja kertoo kaksi kaksinumeroista lukua käyttäen paikka-arvoon ja operaatioiden ominaisuuksiin perustuvia strategioita. Havainnollistaa ja selittää laskutoimituksia käyttämällä yhtälöitä, suorakulmaisia taulukoita ja/tai areamalleja.Huomaa ”ja/tai”. Havainnollistaa laskutoimitusta, mutta riittää, että havainnollistaa sitä yhtälöiden avulla. Sinun ei PITÄÄ havainnollistaa sitä käyttämällä matriiseja.
Tämän sanottuaan, joissakin standardeissa mainitaan tietty visuaalinen malli, kuten numeroviiva tai suorakulmainen aluemalli, mutta se on harvinaisempaa kuin valinnan antaminen, kuten edellä mainituissa standardeissa.
Käsitteellinen matematiikka
Joissakin standardeissa käsitellään matematiikan käsitteellistä puolta, jota peruskoulun opettajat eivät välttämättä ymmärrä, jos heille ei opeteta, mitä ne tarkoittavat; esimerkiksi:
5. NF.7b
Tulkitse kokonaisluvun jakaminen yksikkömurtoluvulla ja laske tällaiset kertoimet. Luo esimerkiksi tarinallinen konteksti 4 ÷ (1/5) ja käytä visuaalista murtolukumallia osoittaaksesi osamäärän. Käytä kerto- ja jakolaskujen välistä suhdetta selittääksesi, että 4 ÷ (1/5) = 20, koska 20 × (1/5) = 4.Yksi tällainen tarinallinen ongelma voisi olla: Kuinka monta 1/5-jalkaa pitkää palaa voit leikata 4-jalkaisesta materiaalipalasta? Visuaalinen malli voisi näyttää 4 kokonaisuutta, jotka on jaettu viidenneksiksi. Voimme sitten laskea, että 4 kokonaisuutta on yhteensä 20 viidesosaa.
5.NF.4b
Löydä sellaisen suorakulmion pinta-ala, jonka sivupituudet ovat murtolukuja, laatoittamalla se yksikköneliöillä, joiden sivupituudet ovat sopivan murtoluvun yksikkömurtoluvun pituisia, ja osoita, että pinta-ala on sama kuin se, joka löytyisi kertomalla sivupituudet. Kertoa murtolukujen sivupituudet suorakulmioiden pinta-alojen löytämiseksi ja esittää murtolukujen tuotteet suorakulmion pinta-aloina.
Tämä tarkoittaa esimerkiksi suorakulmiota, jonka sivupituudet ovat 3/4 km ja 4/5 km. Sitten laatoitamme sen pienillä yksikkösuorakulmioilla (ei yksikköneliöillä; tässä standardissa itsessään on väärä terminologia), joiden jokaisen sivunpituudet ovat 1/4 km ja 1/5 km.
Voimme laskea, kuinka monta pientä laattaa tarvitsemme. Tarvitsemme 12 tällaista laattaa. Jokaisen laatan pinta-ala on 1/20 km2, joten kokonaispinta-ala on 12/20 km2. Sitten tarkistamme ja vertailemme, että saamme saman vastauksen kuin jos olisimme kertoneet kahden sivun pituudet tavallisella murtolukujen kertolaskulla (3/4 km × 4/5 km = 12/20 km2).
Kirjoissani on aina ollut tämäntyyppisiä ongelmia – jo ennen CCS:n tuloa.
Jotkut väittävät, että lapset eivät tarvitse tällaista käsitteellistä ymmärrystä tai että se on liian vaikeaa. Itse olen eri mieltä. Olen aina (myös ennen CCS:ää) pyrkinyt selittämään murtolukujen aritmetiikan käsitteet niin, etteivät oppilaat päädy ”sokeasti noudattamaan sääntöjä” ja pysty laskemaan murtoluvuilla vain, jos he sattuvat muistamaan säännön oikein. Olen aina korostanut käsitteellistä ymmärrystä matematiikassa (kuten lukijani tietävät!).
Mutta toivon, että ymmärrätte, miten jotkut näistä asioista voivat olla vieraita koulujen opettajille ja vanhemmille, eikä siksi ole ihme, että Common Core -standardien noudattaminen on heille vaikeaa.
Toivon, että Math Mammoth Light Blue -sarja ja yksiköt, joita myyn Teachers Pay Teachers- ja Teachers’ Notebook -myymälöissäni, voivat auttaa niitä opettajia & vanhempia, jotka tarvitsevat Common Coren mukaisia materiaaleja. Ja kuten sanoin, myös te muut voitte käyttää niitä luottavaisin mielin. Ne eivät sisällä mitään ”outoa” tai järjetöntä matematiikkaa, vaan kuten aina, ne perustuvat yksinkertaisesti vankalle perustalle, jossa matematiikan käsitteitä opetetaan yhdessä menetelmien kanssa.
Maria Miller