Eulerin identiteetti vaikuttaa hämmentävältä:

Se nousee esiin yleisemmästä kaavasta:

Yowza — suhtaudumme imaginääriseen eksponenttiin ja siniiniin ja kosiniin! Ja jotenkin liittämällä pi saadaan -1? Voiko tämä koskaan olla intuitiivista?

Ei 1800-luvun matemaatikon Benjamin Peircen mukaan:

Se on täysin paradoksaalista; emme voi ymmärtää sitä, emmekä tiedä mitä se tarkoittaa, mutta olemme todistaneet sen, ja siksi tiedämme, että sen täytyy olla totuus.

Argh, tämä asenne saa vereni kiehumaan! Kaavat eivät ole ulkoa opeteltavia taikaloitsuja: meidän täytyy, täytyy, täytyy löytää oivallus. Tässä omani:

Eulerin kaava kuvaa kahta ekvivalenttia tapaa liikkua ympyrässä.

Niinkö? Tässä huikeassa yhtälössä on kyse ympyrän pyörimisestä? Kyllä — ja voimme ymmärtää sen rakentamalla muutaman analogian varaan:

• Alkaen luvusta 1, näe kertolasku muunnoksena, joka muuttaa lukua: $1 \cdot e^{i \pi}$
• Säännöllinen eksponentiaalinen kasvu kasvattaa 1:tä jatkuvasti jollakin nopeudella jonkin ajanjakson ajan; kuvitteellinen eksponentiaalinen kasvu pyörittää 1:tä jatkuvasti jonkin ajanjakson ajan
• Kasvu ”pi”-aikayksiköissä tarkoittaa pi-radiaanien kulkemista ympyrän ympäri
• Siten $e^{i \pi}$ tarkoittaa, että aloitamme 1:stä ja pyöritämme pi:tä (ympyrän puoliväliä) saadaksemme -1:n

Tässä on korkean tason näkemys, sukelletaanpa yksityiskohtiin. Muuten, jos joku yrittää tehdä sinuun vaikutuksen sanomalla $e^{i \pi} = -1$, kysy häneltä i:stä i:n potenssiin. Jos he eivät osaa ajatella asiaa loppuun asti, Eulerin kaava on heille edelleen taikatemppu.

Päivitys: Kirjoittaessani ajattelin, että video voisi auttaa selittämään ajatukset selkeämmin:

Ymmärtäminen cos(x) + i * sin(x)

Yhtäsuuruusmerkki on ylikuormitettu. Joskus tarkoitamme ”asettaa yhden asian toiseen” (kuten x = 3) ja joskus taas ”nämä kaksi asiaa kuvaavat samaa käsitettä” (kuten $\sqrt{-1} = i$).

Eulerin kaava on jälkimmäinen: se antaa kaksi kaavaa, jotka selittävät, miten liikutaan ympyrässä. Jos tarkastelemme ympyräliikettä trigonometrian avulla ja kuljemme x radiaania:

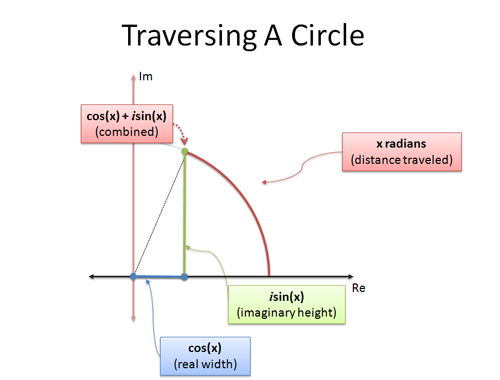
• cos(x) on x-koordinaatti (vaakasuora etäisyys)
• sin(x) on y-koordinaatti (pystysuora etäisyys)

Lausuma

on nokkela tapa sulattaa x- ja y-koordinaatit yhdeksi luvuksi. Analogia ”kompleksiluvut ovat kaksiulotteisia” auttaa meitä tulkitsemaan yhden kompleksiluvun sijainniksi ympyrällä.

Kun asetamme x:n arvoksi $\pi$, kuljemme $\pi$-yksikköä pitkin yksikköympyrän ulkopintaa. Koska kokonaisympyrän ympärysmitta on $2\pi$, tavallinen vanha $\pi$ on puolessa välissä ympyrää, jolloin olemme pisteessä -1.

Neato: Eulerin kaavan oikea puoli ($\cos(x) + i \sin(x)$) kuvaa ympyräliikettä kuvitteellisilla luvuilla. Nyt selvitetään, miten yhtälön e-puoli toteuttaa sen.

Mitä on imaginaarikasvu?

X- ja y-koordinaattien yhdistäminen kompleksiluvuksi on hankalaa, mutta hallittavissa. Mutta mitä imaginaarinen eksponentti tarkoittaa?

Käydäänpä vähän taaksepäin. Kun näen $3^4$, ajattelen sitä näin:

• 3 on lopputulos, kun se kasvaa välittömästi (e:n avulla) nopeudella ln(3). Toisin sanoen: $3 = e^{\ln(3)}$
• $3^4$ on sama kuin kasvaisi 3:een, mutta kasvaisi sitten 4x yhtä kauan. Siis $3^4 = e^{\ln(3) \cdot 4} = 81$

Sen sijaan, että näkisit luvut sellaisenaan, voit ajatella niitä joksikin, mihin e:n piti ”kasvaa”. Reaaliluvut, kuten 3, antavat koron ln(3) = 1,1, ja sitä e ”kerää” mennessään, kasvaessaan jatkuvasti.

Säännöllinen kasvu on yksinkertaista: se ”työntää” lukua jatkuvasti samaan, todelliseen suuntaan, johon se oli menossa. 3 × 3 työntää alkuperäiseen suuntaan tehden siitä kolme kertaa suuremman (9).

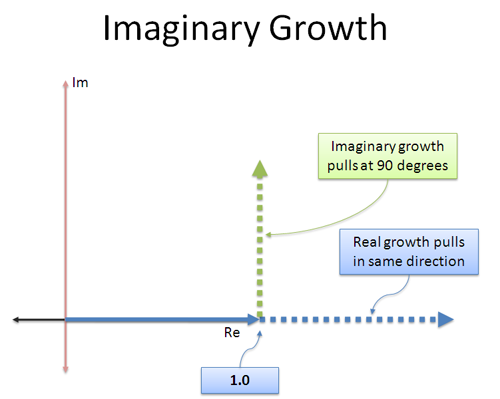
Imaginaarinen kasvu on erilaista: ansaitsemamme ”korko” on eri suuntaan! Se on kuin suihkumoottori, joka on kiinnitetty sivuttain — sen sijaan, että menisimme eteenpäin, alamme työntää 90 asteen kulmassa.

Kiva asia jatkuvassa ortogonaalisessa (kohtisuorassa) työntämisessä on se, että se ei nopeuta tai hidasta sinua — se pyörittää sinua! Minkä tahansa luvun ottaminen ja kertominen i:llä ei muuta sen suuruutta, vain suuntaa, johon se osoittaa.

Intuitiivisesti näin näen jatkuvan kuvitteellisen kasvunopeuden: ”Kun kasvan, älä työnnä minua eteenpäin tai taaksepäin siihen suuntaan, johon olen jo menossa. Pyöritä minua sen sijaan.”

Mutta eikö meidän pitäisi pyöriä yhä nopeammin ja nopeammin?

Tätäkin mietin. Säännöllinen kasvu yhdistyy alkuperäiseen suuntaamme, joten menemme 1, 2, 4, 8, 16, kerrottuna 2x joka kerta ja pysyen reaaliluvuissa. Voimme ajatella tätä $e^{\ln(2)x}$, mikä tarkoittaa, että kasvamme välittömästi nopeudella ln(2) ”x” sekunnin ajan.

Ja hei — jos kasvunopeutemme olisi kaksi kertaa nopeampi, 2ln(2) vs. ln(2), se näyttäisi samalta kuin se, että kasvaisimme kaksi kertaa kauemmin (2x vs. x). E:n taika antaa meidän vaihtaa nopeuden ja ajan keskenään; 2 sekuntia ln(2):lla on sama kasvu kuin 1 sekunti 2ln(2):lla.

Kuvitellaan nyt, että meillä on jokin puhtaasti kuvitteellinen kasvuvauhti (Ri), joka pyörittää meitä, kunnes saavutamme i:n eli 90 astetta ylöspäin. Mitä tapahtuu, jos kaksinkertaistamme tuon nopeuden 2Ri:iin, pyörähdämmekö pois ympyrästä?

Ei! Kun nopeus on 2Ri tarkoittaa, että pyörimme vain kaksi kertaa nopeammin, tai vaihtoehtoisesti pyörimme nopeudella R kaksi kertaa kauemmin, mutta pysymme ympyrällä. Pyöriminen kaksi kertaa yhtä kauan tarkoittaa, että olemme nyt 180 astetta päin.

Kun huomaamme, että jokin eksponentiaalinen kasvuvauhti voi viedä meidät arvosta 1 arvoon i, tuon nopeuden kasvattaminen vain pyörittää meitä enemmän. Emme pääse koskaan pois ympyrästä.

Vaikka jos kasvuvauhtimme on kompleksinen (a+bi vs Ri), niin reaaliosa (a) kasvattaa meitä normaalisti, kun taas imaginääriosa (bi) pyörittää meitä. Mutta ei mennä nyt hienostelemaan: Eulerin kaavassa $e^{ix}$ on kyse puhtaasti imaginaarisesta kasvusta, joka pitää meidät ympyrällä (lisää myöhemmin).

Pikainen tervejärkisyystarkastus

Kirjoittaessani jouduin selventämään itselleni muutaman kysymyksen:

Miksi käyttää $e^{ix}$:tä, emmekö pyöritä lukua 1?

e edustaa prosessia, joka alkaa arvosta 1 ja kasvaa jatkuvasti 100 %:n korolla yhden aikayksikön ajan.

Kirjoittaessamme e vangitsemme koko prosessin yhteen ainoaan lukuun — e edustaa koko jatkuvan kasvun takkuilua. Todellisuudessa $e^x$ sanoo siis ”aloita 1:stä ja kasva jatkuvasti 100 %:lla x sekunnin ajan”, ja se alkaa 1:stä, kuten haluamme.

Mutta mitä i eksponenttina tekee?

Säännölliselle eksponentille, kuten $3^4$, kysymme:

• Mikä on implisiittinen kasvunopeus? Kasvamme 1:stä 3:een (eksponentin pohjaan).
• Miten muutamme tuota kasvunopeutta? Skaalaamme sen 4x:llä (eksponentin potenssilla).

Voidaan muuntaa kasvumme ”e”-muotoon: hetkellinen kasvuvauhtimme on ln(3), ja kasvatamme sen arvoon ln(3) * 4. Jälleen eksponentin potenssi (4) juuri skaalasi kasvuvauhtimme.

Kun ylimmäinen eksponentti on i (kuten $3^i$:ssä), kerromme implisiittisen kasvuvauhtimme vain i:llä. Sen sijaan, että kasvaisimme tavallisella vanhalla ln(3):lla, kasvamme siis ln(3) * i:llä.

Yläosan eksponentin yläosa muuttaa alaosan implisiittistä kasvuvauhtia.

Tarkat yksityiskohdat

Katsotaanpa tarkemmin. Muista tämä e:n määritelmä:

Tämä $\frac{100\%}{n}$ edustaa sitä korko-osuutta, jonka ansaitsimme kullakin mikroskooppisella jaksolla. Oletimme, että korko oli 100 % reaaliulottuvuudessa — mutta entä jos se olisikin 100 % imaginaarisessa suunnassa?

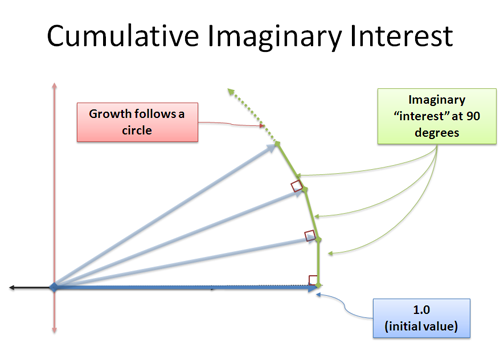
Nyt vastamuodostunut korkomme lisää meille 90 asteen suunnassa. Yllättäen tämä ei muuta pituuttamme – tämä on hankala käsite, koska se näyttää tekevän kolmion, jossa hypotenuusan on oltava suurempi. Olemme tekemisissä rajan kanssa, ja ylimääräinen etäisyys on määrittelemämme virhemarginaalin sisällä. Tähän haluan puuttua jonain toisena päivänä, mutta uskokaa minua: jatkuva kohtisuora kasvu pyörittää teitä. Tämä on sinin ja kosinin ydin, jossa muutos on kohtisuorassa nykyiseen sijaintiisi nähden, ja liikut ympyrää pitkin.

Sovellamme i yksikköä kasvua äärettömän pienissä askelissa, joista jokainen työntää meitä 90 asteen kulmassa. Mitään ”yhä nopeampaa ja nopeampaa” pyörimistä ei tapahdu – sen sijaan ryömimme kehää pitkin matkan |i| = 1 (i:n suuruus).

Ja hei — ympyrän ympäri ryömitty matka on kulma radiaaneina! Olemme löytäneet toisen tavan kuvata ympyräliikettä!

Taakseen ympyräliikkeen: Muutetaan jatkuvasti kiertämällä 90 asteen kulmassa (eli imaginaarinen kasvunopeus).

Eulerin kaava sanoo siis ”eksponentiaalinen, imaginaarinen kasvu jäljittää ympyrän”. Ja tämä polku on sama kuin liikkuminen ympyrässä käyttäen siniä ja kosinia kuvitteellisessa tasossa.

Tässä tapauksessa sana ”eksponentiaalinen” on hämmentävä, koska kuljemme ympyrän ympäri vakionopeudella. Useimmissa keskusteluissa eksponentiaalisella kasvulla oletetaan olevan kumulatiivinen, kasautuva vaikutus.

Joitakin esimerkkejä

Et taida oikeasti uskoa minua? Tässä muutama esimerkki ja miten niitä voi ajatella intuitiivisesti.

Esimerkki: $e^i$

Missä on x? Ah, se on vain 1. Intuitiivisesti, ilman laskinta, tiedämme, että tämä tarkoittaa ”kulje 1 radiaani pitkin yksikköympyrää”. Päässäni näen ”e”:n yrittävän kasvaa 1:llä 100 %:lla kaikki samaan suuntaan, mutta i jatkaa pallon liikuttamista ja pakottaa ”1:n” kasvamaan ympyrän reunaa pitkin:

Ei mikään kaunein luku, mutta siinä se on. Muista laittaa laskimesi radiaani-tilaan, kun lyöt tämän sisään.

Esimerkki: $3^i$

Tämä on hankalaa — se ei ole vakiomuodossamme. Mutta muista,

Haluamme alkukasvun olevan 3x jakson lopussa eli hetkellisen kasvunopeuden olevan ln(3). Mutta, i tulee ja muuttaa tuon nopeuden ln(3) muotoon ”i * ln(3)”:

Luulimme, että muunnumme säännöllisellä nopeudella ln(3), hieman nopeammin kuin 100 %:n jatkuvalla kasvulla, koska e on noin 2,718. Mutta voi ei, minä pyöräytin meidät ympäri: nyt me muunnumme kuvitteellisella nopeudella, mikä tarkoittaa, että me vain pyörimme ympäri. Jos i olisi säännöllinen luku kuten 4, se olisi saanut meidät kasvamaan 4x nopeammin. Nyt kasvamme nopeudella ln(3), mutta sivusuunnassa.

Meidän pitäisi odottaa kompleksilukua yksikköympyrällä – kasvunopeudessa ei ole mitään, mikä kasvattaisi kokoamme. Yhtälön ratkaiseminen:

Siten sen sijaan, että päätyisimme ”1” yksikön ympyrän ympäri (kuten $e^i$), päädymme ln(3) yksikön ympäri.

Esimerkki: $i^i$

Muutama kuukausi sitten tämä olisi saanut minut itkemään. Ei enää tänään! Puretaan muunnokset:

Aloitamme luvulla 1 ja haluamme muuttaa sitä. Kuten ratkaista $3^i$, mikä on hetkellinen kasvuvauhti, jota i edustaa pohjana?

Hm. Normaalisti tekisimme ln(x) saadaksemme kasvunopeuden, joka tarvitaan x:n saavuttamiseen 1 aikayksikön lopussa. Mutta kuvitteelliselle nopeudelle? Meidän on nuudeloitava tätä.

Aloittaaksemme arvosta 1 ja kasvaaksemme arvoon i meidän on aloitettava pyöriminen alusta. Kuinka nopeasti? No, meidän on saatava 90 astetta (pi/2 radiaania) yhdessä aikayksikössä. Nopeutemme on siis $i \frac{\pi}{2}$. Muista, että nopeutemme on oltava kuvitteellinen, koska pyörimme, emme kasva! Tavallinen vanha $\frac{\pi}{2}$ on noin 1.57 ja johtaa säännölliseen kasvuun.

Tässä pitäisi olla järkeä: kääntääksemme 1.0:n i:ksi yhden yksikön lopussa, meidän pitäisi kiertää $\frac{\pi}{2}$ radiaania (90 astetta) kyseisessä ajassa. Saadaksemme ”i” voimme siis käyttää $e^{i \frac{\pi}{2}}$.

Phew. Se kuvaa i:tä peruslukuna. Entä eksponentti?

Noh, toinen i kertoo, että meidän on muutettava kurssia – kyllä, sitä kurssia, jonka selvittämiseen käytimme niin kauan aikaa! Joten sen sijaan, että pyörisimme nopeudella $i \frac{\pi}{2}$, mitä i:n perusta tarkoittaa, muutamme nopeuden muotoon:

i:t peruuntuvat ja tekevät kasvuvauhdista jälleen todellisen! Käänsimme nopeutemme ja työnsimme itsemme negatiivisiin lukuihin. Ja negatiivinen kasvuvauhti tarkoittaa, että kutistumme – meidän pitäisi odottaa $i^i$:n pienentävän asioita. Ja niin se tekeekin:

Tada! (Etsi ”i^i” Googlella käyttääksesi sen laskuria)

Hengähdä hetki: Voit intuitiivisesti selvittää, miten imaginaaristen emästen ja imaginaaristen eksponenttien pitäisi käyttäytyä. Whoa.

Ja bonuksena keksit ln(i) — saadaksesi $e^x$:n muuttumaan i:ksi, tee e:stä pyörähdys $\frac{\pi}{2}$ radiaania.

Example: (i^i)^i

Kaksinkertainen imaginaarieksponentti? Jos sinä vaadit. Ensinnäkin tiedämme, mikä kasvuvauhtimme on sulkujen sisällä:

Saamme negatiivisen (kutistuvan) kasvuvauhdin -pi/2. Ja nyt muutamme tuota nopeutta taas i:llä:

Ja nyt meillä on negatiivinen kierto! Kuljemme ympyrän ympäri nopeudella $-\frac{\pi}{2}$ aikayksikköä kohti. Kuinka kauan kuljemme? Tämän eksponenttiketjun huipulla on implisiittinen aikayksikkö ”1”; implisiittinen oletusarvo on, että mennään yhden aikayksikön ajan (aivan kuten $e = e^1$). Yksi aikayksikkö antaa meille $-\frac{\pi}{2}$ radiaania (-90 astetta) tai -i!

Ja, ihan vain huvin vuoksi, jos neliöisimme tuon hullun tuloksen:

Se on ”vain” kaksi kertaa suurempi pyörimisnopeus: 2 on säännönmukainen luku, joten se tuplataakin pyörimisnopeutemme täyteen -180 astetta aikayksikössä. Tai voit tarkastella sitä niin, että sovellamme -90 asteen kiertoa kahdesti peräkkäin.

Ensi silmäyksellä nämä ovat todella outoja eksponentteja. Mutta analogioidemme avulla voimme ottaa ne rennosti.

Kompleksinen kasvu

Meitä voi olla reaalinen ja imaginaarinen kasvu samanaikaisesti: reaalinen osa skaalaa meitä ylöspäin, ja imaginaarinen osa kiertää meitä ympäri:

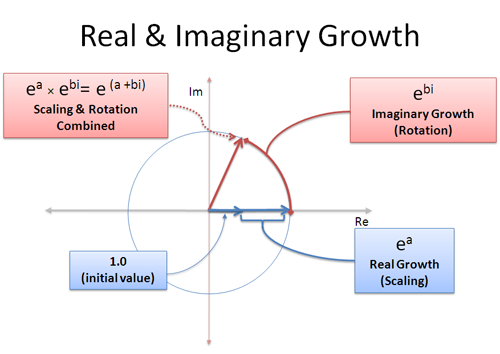
Kompleksinen kasvunopeus, kuten (a + bi), on sekoitus reaalista ja imaginaarista kasvua. Reaaliosa a, tarkoittaa ”kasva 100 %:lla a sekuntia” ja imaginääriosa b tarkoittaa ”pyörii b sekuntia”. Muista, että rotaatiot eivät saa yhdistämisen etua, koska jatkat ”työntämistä” eri suuntaan — rotaatio summautuu lineaarisesti.

Tämä mielessä, voimme esittää minkä tahansa pisteen minkä tahansa kokoisella ympyrällä käyttäen (a+bi)! Säde on $e^a$ ja kulma määräytyy $e^{bi}$. Se on kuin laittaisi luvun expand-o-troniin kahdeksi sykliksi: kerran sen kasvattamiseksi oikeaan kokoon (a sekuntia) ja toisen kerran sen kiertämiseksi oikeaan kulmaan (b sekuntia). Tai voisit kiertää sen ensin ja sitten kasvattaa!

Esitettäköön, että haluamme tietää kasvun määrän, jolla saamme 6 + 8i. Tässä kysytään oikeastaan kuvitteellisen luvun luonnollista logia: miten kasvatamme e:tä saadaksemme (6 + 8i)?

• Säde: Kuinka suuren ympyrän tarvitsemme? No, suuruus on $\sqrt{6^2 + 8^2} = \sqrt{100} = 10$. Tämä tarkoittaa, että meidän täytyy kasvaa ln(10) = 2,3 sekuntia saavuttaaksemme tämän määrän.
• Kierrettävä määrä: Mikä on tuon pisteen kulma? Voimme käyttää arctania sen selvittämiseen: atan(8/6) = 53 astetta = 0,93 radiaania.
• Yhdistetään tulos: ln(6+8i) = 2,3 + 0,93i

Tämä tarkoittaa, että voimme saavuttaa satunnaisen pisteen (6 + 8i), jos käytämme $e^{2.3 + .93i}$.

Miksi tämä on hyödyllistä?

Eulerin kaava antaa meille toisen tavan kuvata liikettä ympyrässä. Mutta voisimme jo tehdä sen sinin ja kosinin avulla — mikä siinä on niin erikoista?

Kyse on näkökulmasta. Sini ja kosini kuvaavat liikettä ruudukon avulla, piirtämällä vaaka- ja pystysuorat koordinaatit.

Eulerin kaava käyttää polaarikoordinaatteja — mikä on kulma ja etäisyys? Taas kaksi tapaa kuvata liikettä:

• Ruudukkojärjestelmä: Mene 3 yksikköä itään ja 4 yksikköä pohjoiseen
• Polaarikoordinaatit: Mene 5 yksikköä 53,13 asteen kulmassa

Riippuen ongelmasta, polaari- tai suorakulmaiset koordinaatit ovat hyödyllisempiä. Eulerin kaavan avulla voimme muuntaa näiden kahden välillä, jotta voimme käyttää tehtävään parhaiten soveltuvaa työkalua. Koska $e^{ix}$ voidaan muuntaa siniksi ja kosiniksi, voimme myös kirjoittaa trigonometriset kaavat uudelleen e:n muunnoksina, mikä on erittäin kätevää (ei tarvitse opetella ulkoa sin(a+b):tä, voit johtaa sen – lisää joku toinen päivä). Ja on kaunista, että jokainen luku, reaalinen tai kompleksinen, on e:n muunnos.

Mutta hyöty, schmutility: tärkein tulos on oivallus siitä, että hämmentävistä yhtälöistä voi tulla intuitiivisia oikeiden analogioiden avulla. Älä anna Eulerin kaavan kaltaisten kauniiden yhtälöiden jäädä taikatauluksi — rakenna tuntemiesi analogioiden varaan nähdäksesi yhtälön sisällä olevat oivallukset.

Happy math.

Liite

Screencast oli hauska, ja palaute on ehdottomasti tervetullutta. Mielestäni se auttaa ideoita ponnahtamaan esiin, ja artikkelin läpikäyminen auttoi minua löytämään aukkoja intuitiossani.

• Brian Slesinskylla on siisti esitys Eulerin kaavasta
• Visual Complex Analysisissa on hieno keskustelu Eulerin kaavasta — ks. s. 10 Googlen kirjojen esikatselussa
• Pidin esityksen Math and Analogies, jossa selitän Eulerin identiteettiä visuaalisemmin:

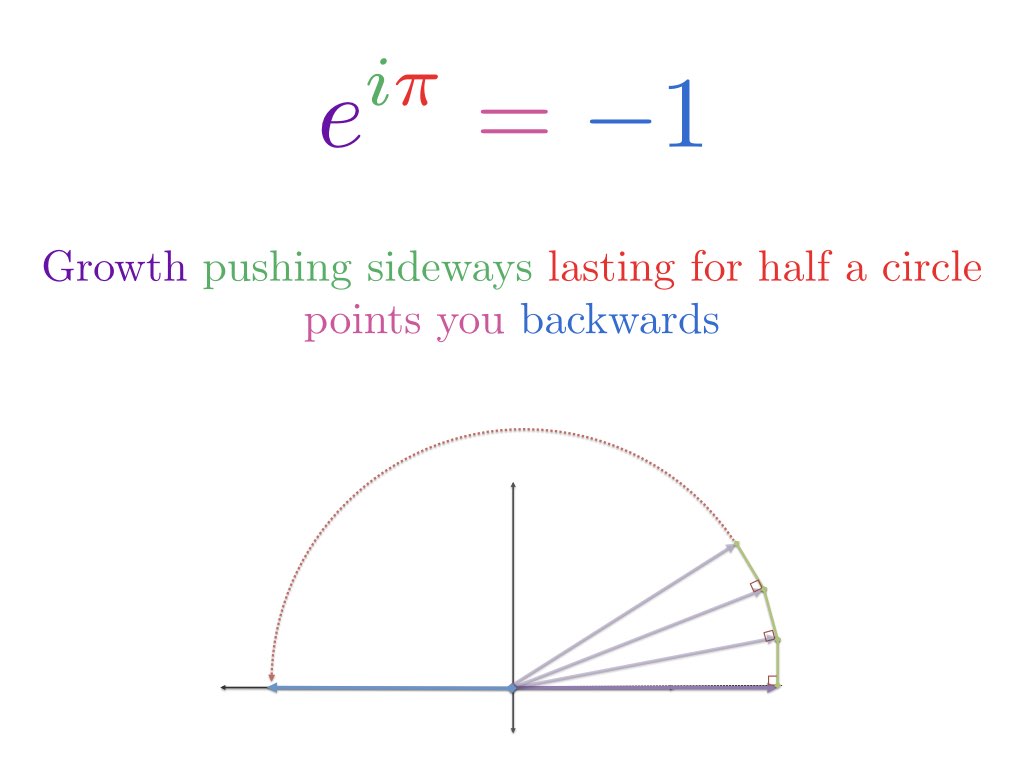
Other Posts In This Series

1. Visuaalinen, intuitiivinen opas mielikuvituslukuihin
2. Intuitiivinen aritmetiikka kompleksiluvuilla
3. Ymmärtää, miksi kompleksikertolaskutoimitus toimii
4. Intuitiivinen opas kulmiin, Degrees and Radians
5. Intuitive Understanding Of Euler’s Formula
6. An Interactive Guide To The Fourier Transform
7. Intuitive Guide to Convolution
8. Intuitiivinen ymmärrys siniaalloista
9. Intuitiivinen opas lineaarialgebraan
10. Ohjelmoijan intuitio matriisien kertomiseen
11. Imaginary Multiplication vs. Kuvitteelliset eksponentit