P-Only-säätimen tavoin Proportionaalinen-Integraalinen (PI) algoritmi laskee ja lähettää säätimen ulostulosignaalin (CO-signaalin) joka näytteenottokerralla T lopulliselle ohjauselementille (esim. venttiili, taajuusmuuttajapumppu). PI-algoritmin laskemaan CO-signaaliin vaikuttavat säätimen viritysparametrit ja säätimen virhe, e(t).
PI-säätimissä on kaksi säädettävää viritysparametria. Vaikka tämä tekee niiden virittämisestä haastavampaa kuin pelkän P-säätimen, ne eivät ole yhtä monimutkaisia kuin kolmen parametrin PID-säädin.
Integraalisen toiminnan ansiosta PI-säätimet poistavat offsetin, joka on pelkän P-säätimen suuri heikkous. Näin ollen PI-säätimet tarjoavat tasapainon monimutkaisuuden ja kyvykkyyden välillä, mikä tekee niistä ylivoimaisesti yleisimmin käytetyn algoritmin prosessinohjaussovelluksissa.
PI-algoritmi
Vaikka eri toimittajat valavat pohjimmiltaan saman algoritmin eri muodoissa, tarkastelemme tässä sitä, mitä on eri tavoin kuvattu riippuvaiseksi, ihanteelliseksi, jatkuvaksi, aseman muodoksi:
![]()
Missä:
CO = säätimen lähtösignaali (johto ulos)
CObias = säätimen bias tai nolla-arvo; asetetaan puskurittomalla siirrolla, kuten jäljempänä selitetään
e(t) = nykyisen säätimen virhe, joka on määritelty seuraavasti: SP – PV
SP = asetusarvo
PV = mitattu prosessimuuttuja (wire in)
Kc = säätimen vahvistus, viritysparametri
Ti = nollausaika, viritysparametri
Kaksi ensimmäistä termiä yhtäsuuruusesimerkin oikealla puolella ovat identtiset tämän artikkelin yläosassa referoidun P-Only-regulaattoriin kanssa.
Säätimen integraalitila on yhtälön viimeinen termi. Sen tehtävänä on integroida tai laskea jatkuvasti yhteen säätimen virhe, e(t), ajan funktiona.
Joitakin asioita, jotka on hyvä tietää nollausajan viritysparametrista Ti:
| ▪ | Se antaa integraalitermille erillisen painoarvon, joten integraalitoiminnan vaikutusta voidaan säätää itsenäisesti. |
| ▪ | Se on nimittäjässä, joten pienemmät arvot antavat suuremman painoarvon (esim. lisäävät) integraalitermin vaikutusta. |
| ▪ | Se on aikayksikkö, joten se on aina positiivinen. |
Suhteellisen termin funktio
Kuten P-Only-säätimessä, PI-säätimen suhteellinen termi Kc-e(t) lisää tai vähentää CObiasista sen mukaan, kuinka suuri säätimen virhe e(t) on kullakin ajanhetkellä t.
Kun e(t) kasvaa tai pienenee, CObiasiin lisättävä määrä kasvaa tai pienenee välittömästi ja suhteellisesti. Säätimen virheen aiemmalla historialla ja nykyisellä liikeradalla ei ole vaikutusta proportionaalitermin laskentaan.
Oheinen kuvaaja (klikkaamalla saat suuren näkymän) havainnollistaa tätä ajatusta asetusarvovasteen osalta. Proportionaalilaskennassa käytetty virhe näkyy kuvaajassa:
▪ Ajankohtana t = 25 min, e(25) = 60-56 = 4
▪ Ajankohtana t = 40 min, e(40) = 60-62 = -2
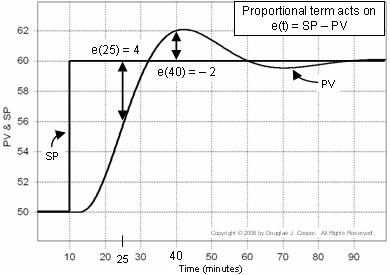
Toteamalla, että säätimen virhe e(t) = SP – PV, sen sijaan, että tarkastelemme PV:tä ja SP:tä erillisinä jälkikäteen, kuten edellä, voimme laskea ja piirtää kuvaajassa e(t) kullakin ajankohdalla t.
Alhaalla (klikkaamalla saat suuren näkymän) on identtiset tiedot kuin edellä, mutta se on esitetty uudelleen e(t):n itsensä kuvaajana. Huomaa, että yllä olevassa kuvaajassa PV = SP = 50 ensimmäisten 10 minuutin ajan, kun taas alla olevassa virheen kuvaajassa e(t) = 0 samalla ajanjaksolla.
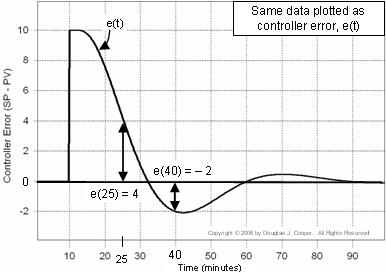
Tämä kuvaaja on hyödyllinen, koska sen avulla voimme havainnollistaa, miten säätimen virhe muuttaa jatkuvasti kokoa ja esimerkkiä ajan myötä.
Integraalitermin funktio
Mikäli proportionaalitermi huomioi e(t):n senhetkisen suuruuden vain säätimen laskentahetkellä, integraalitermi huomioi virheen historian eli sen, kuinka kauan ja kuinka kaukana mitattu prosessimuuttuja on ollut asetuspisteestä ajan mittaan.
Integraali on jatkuvaa summaamista. Virheen integrointi ajan funktiona tarkoittaa, että summataan koko säätimen virhehistoria nykyhetkeen asti, alkaen siitä, kun säädin kytkettiin ensimmäisen kerran automaattiseksi.
Säätimen virhe on e(t) = SP – PV. Alla olevassa kuvaajassa (klikkaamalla saat suuren näkymän) virheen integraalisumma lasketaan SP- ja PV-jälkien väliin jäävinä tummennettuina alueina.
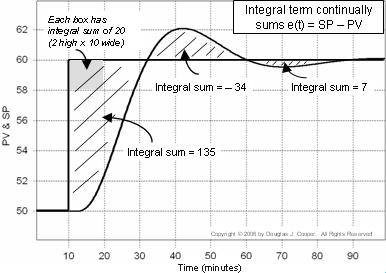
Jokaiseen kuvaajan laatikkoon on merkitty 20:n integraalisumma (2 korkeaa ja 10 leveää). Jos laskemme tummennettujen alueiden sisältämien laatikoiden lukumäärän (mukaan lukien laatikoiden murto-osat), voimme laskea virheen integraalisumman.
Silloin kun PV ylittää ensimmäisen kerran asetuspisteen noin klo t = 32, integraalisumma on kasvanut noin 135:een. Kirjoitamme PI-säätimen integraalitermin seuraavasti:
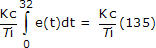
Koska laskutoimitusta ohjaa säätimen virhe, saamme suoran kuvan tilanteesta säätimen virheen kuvaajasta alla olevan kuvan mukaisesti (klikkaamalla saat isomman näkymän):

Huomaa, että jokaisen tummennetun osan integraalilla on sama esimerkki kuin virheellä. Koska integraalisumma alkaa kertyä, kun säädin asetetaan ensimmäistä kertaa automaattiseen toimintaan, kokonaisintegraalisumma kasvaa niin kauan kuin e(t) on positiivinen ja kutistuu, kun se on negatiivinen.
Ajankohtana t = 60 min kuvaajissa integraalisumma on 135 – 34 = 101. Vaste on suurelta osin tasaantunut ajankohtana t = 90 min, ja integraalisumma on tällöin 135 – 34 + 7 = 108.
Integraalinen vaikutus poistaa offsetin
Edellisessä lauseessa tehdään hienovarainen, mutta erittäin tärkeä havainto. Vastaus on suurelta osin valmis ajankohtana t = 90 min, mutta silti kaikkien virheiden integraalisumma ei ole nolla.
Tässä esimerkissä integraalisumman loppu- tai jäännösarvo on 108. Juuri tämä jäännösarvo mahdollistaa PI-säätimen integraalisen toiminnan offsetin eliminoimiseksi.
Kuten aiemmassa artikkelissa käsiteltiin, useimmat prosessit, joissa käytetään pelkkää P-säätöä, kokevat offsetia normaalin toiminnan aikana. Offset on jatkuva arvo säätimen virheelle (eli PV ei ole yhtä suuri kuin SP vakaassa tilassa).
Tunnistamme P-only-säätimestä:
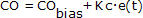
että CO on aina yhtä suuri kuin CObias, ellemme lisää tai vähennä siitä jotakin.
Ainut tapa, jolla meillä on jotakin lisättävää tai vähennettävää CObiasista yllä olevassa P-only-yhtälössä, on se, että e(t) ei ole nolla. Jos e(t) ei ole tasaisesti nolla, PV ei ole yhtä suuri kuin SP ja meillä on offset.
Mutta PI-säätimellä:
![]()
tietäämme nyt, että integraalivirheiden summalla voi olla loppu- tai jäännösarvo sen jälkeen, kun vaste on valmis. Tämä on tärkeää, koska se tarkoittaa, että e(t) voi olla nolla, mutta meillä voi silti olla jotain lisättävää tai vähennettävää CObiasta, jotta voimme muodostaa lopullisen säätimen ulostulon CO.
Sikäli kuin virhettä on (niin kauan kuin e(t) ei ole nolla), integraaliehdon koko kasvaa tai pienenee vaikuttaen CO:hon. Muutokset CO:ssa loppuvat vasta, kun PV on yhtä suuri kuin SP (kun e(t) = 0) kestävän ajanjakson ajan.
Tällöin integraalitermillä voi olla jäännösarvo, kuten juuri keskusteltiin. Tämä integraation jäännösarvo, kun se lisätään CObiasiin, luo olennaisesti uuden yleisen bias-arvon, joka vastaa uutta toimintatasoa.
Tosiasiassa integraalitoiminta nollaa jatkuvasti bias-arvon offsetin poistamiseksi toimintatason muuttuessa.
PI-säädön haasteet
PI-algoritmin käyttöön liittyy haasteita:
| ▪ | Kahden viritysparametrin vuorovaikutus on vuorovaikutuksessa keskenään, ja suunnittelijan on tasapainotettava niiden vaikutus. |
| ▪ | Integraalinen termi pyrkii lisäämään prosessin vasteen värähtelevää tai rullaavaa käyttäytymistä. |
Koska nämä kaksi viritysparametria ovat vuorovaikutuksessa toistensa kanssa, voi olla haastavaa päästä ”parhaisiin” viritysarvoihin. Suunnittelu- ja viritysreseptimme arvo ja merkitys kasvaa, kun säätimestä tulee monimutkaisempi.
Säätimen alustaminen puskuritonta siirtoa varten
Kun vaihdamme minkä tahansa säätimen manuaalisesta tilasta automaattiseen tilaan (avoimesta silmukasta suljettuun silmukkaan), haluamme lopputuloksen olevan tapahtumaton. Toisin sanoen emme halua, että siirtyminen aiheuttaa äkillisiä säätötoimia, jotka vaikuttavat tai häiritsevät prosessiamme
Saavutamme tämän halutun lopputuloksen siirtymisen yhteydessä alustamalla säätimen integraalivirhesumman nollaan. Myös asetusarvo ja säätimen bias-arvo alustetaan asettamalla:
▪ SP yhtä suureksi kuin nykyinen PV
▪ CObias yhtä suureksi kuin nykyinen CO
Kun virheen integraalisumma on asetettu nollaan, CObiasiin ei ole mitään lisättävää tai vähennettävää, joka aiheuttaisi äkillisen muutoksen säätimen nykyisessä lähdössä. Kun asetusarvo on yhtä suuri kuin mitattu prosessimuuttuja, ei ole mitään virhettä, joka aiheuttaisi muutoksen CO-arvossamme. Ja kun säätimen bias on asetettu nykyiseen CO-arvoon, olemme oletusarvoisesti valmiita säilyttämään nykyisen toiminnan.
Siten kun siirrymme manuaalisesta tilasta automaattiseen tilaan, meillä on ”puskuriton siirto” ilman yllätyksiä. Tämä on tulos, jota kaikki arvostavat.
Nollausaika vs. nollausnopeus
Eri myyjät valavat ohjausalgoritmejaan hieman eri muodoissa. Jotkut käyttävät suhteellista kaistaa säätimen vahvistuksen sijasta. Jotkut käyttävät myös nollausnopeutta, Tr, nollausajan sijasta. Nämä ovat yksinkertaisesti toistensa käänteislukuja:
Tr = 1/Ti
Mitä tahansa viritysparametrit ilmaistaankin, PI-algoritmit ovat kaikki yhtä kyvykkäitä.
Mutta on ratkaisevan tärkeää tuntea valmistajasi, ennen kuin aloitat säätimen virittämisen, koska parametrien arvot on sovitettava tiettyyn algoritmimuotoon.Kaupalliset ohjelmistot säätimien suunnittelua ja virittämistä varten ratkaisevat tämän ongelman automaattisesti puolestasi.
PI-säätimen toteuttaminen
Tarkastelemme PI-säätimen suunnittelua, virittämistä ja toteuttamista lämmönvaihtimella tässä artikkelissa ja painovoimaisesti tyhjennetyillä säiliöillä tässä artikkelissa.