Kuvittele neliö paperia pöydälläsi tasaisesti makaamassa. Pyydän sinua sulkemaan silmäsi. Kuulet paperin liikkuvan. Kun avaat silmäsi, paperi ei näytä muuttuneen. Mitä olen voinut tehdä sille sillä aikaa, kun et katsonut?

On selvää, etten ole kääntänyt paperia 30 astetta, koska silloin paperi näyttäisi erilaiselta.

Ei myöskään ole käännetty paperia poikki viivan yli, joka yhdistää vaikkapa jonkun kulman jonkin toisen reunan puoliväliin. Paperi näyttäisi erilaiselta, jos olisin tehnyt niin.

Mitä olisin kuitenkin voinut tehdä, oli kääntää paperia myötä- tai vastapäivään millä tahansa 90 asteen monikertoimella tai kääntää sen jommankumman diagonaaliviivan tai vaaka- ja pystysuuntaisten viivojen yli.

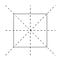
Hyödyllinen tapa havainnollistaa muunnoksia on merkitä neliön kulmat.

Viimeinen vaihtoehto on se, että ei tee mitään. Tätä kutsutaan identiteettimuunnokseksi. Yhdessä näitä kaikkia kutsutaan neliön symmetriamuunnoksiksi.

Voin yhdistää symmetriamuunnoksia toisten symmetriamuunnosten tekemiseksi. Esimerkiksi kaksi kääntöä viivapätkän BD poikki tuottaa identiteetin, samoin kuin neljä peräkkäistä 90 asteen kiertoa vastapäivään. Kääntäminen pystysuoran viivan ympäri ja sen jälkeen kääntäminen vaakasuoran viivan ympäri vaikuttaa samoin kuin 180 asteen kierto. Yleisesti ottaen mikä tahansa symmetriamuunnosten yhdistelmä tuottaa symmetriamuunnoksen. Seuraavassa taulukossa on esitetty symmetriamuunnosten koostamissäännöt:

Tässä taulukossa R, jonka alaviitteet ovat 90, 180 ja 270, tarkoittaa 90, 180 ja 270 asteen käännöksiä vastapäivään, H tarkoittaa käännöksiä vaakasuoran viivan ympäri, V käännöksiä pystysuoran viivan ympäri, MD käännöksiä diagonaalin ympäri vasemmalta ylhäältä oikealle alhaalle ja OD käännöksiä toisen diagonaalin ympäri. Kun haluat löytää A:n ja B:n tulon, siirry A:n riville ja sitten B:n sarakkeeseen. Esimerkiksi H∘MD=R₉₀.

Taulukkoa tarkastelemalla voit huomata muutamia asioita:

• Operaatio ∘ on assosiatiivinen, mikä tarkoittaa, että A∘(B∘C) = (A∘B)∘C kaikille muunnoksille A, B ja C.
• Mille tahansa symmetriamuuntajaparille A ja B myös kompositio A∘B on symmetriamuuntaja
• On olemassa yksi alkio e, joka on sellainen, että A∘e=e∘A jokaiselle A:lle
• Jokaista symmetriamuuntajaa A varten, on olemassa yksikäsitteinen symmetriamuunnos A-¹ siten, että A∘A-¹=A-¹∘A=e

Sanomme siis, että neliön symmetriamuunnosten kokoelma yhdessä komposition kanssa muodostaa matemaattisen rakenteen, jota kutsutaan ryhmäksi. Tätä ryhmää kutsutaan D₄:ksi, neliön dihedriryhmäksi. Nämä rakenteet ovat tämän artikkelin aiheena.

Ryhmän määritelmä

Ryhmä ⟨G,*⟩ on joukko G, jolla on sääntö * minkä tahansa kahden G:n elementin yhdistämiseen, joka täyttää ryhmäaksioomat:

Abstraktissa tekstissä jätämme usein *:n pois ja kirjoitamme a*b:n ab:ksi ja viittaamme *:aan kertolaskuna.

Ei ole välttämätöntä, että * on kommutatiivinen eli a*b=b*a. Tämän näkee katsomalla taulukkoa D₄, jossa H∘MD=R₉₀ mutta MD∘H=R₂₇₀. Ryhmiä, joissa * on kommutatiivinen, kutsutaan Neils Abelin mukaan abelialaisiksi ryhmiksi.

Abelialaiset ryhmät ovat pikemminkin poikkeus kuin sääntö. Toinen esimerkki ei-abeliaanisesta ryhmästä on kuution symmetriamuunnokset. Tarkastellaan vain kiertoja akselien ympäri:

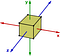
Jos käännän ensin 90 astetta vastapäivään y-akselin ympäri ja sitten 90 astetta vastapäivään z-akselin ympäri, niin hänen tuloksensa on erilainen kuin jos käännän 90 astetta z-akselin ympäri ja sitten 90 astetta y-akselin ympäri.

Elementin on mahdollista olla oma käänteisensä. Tarkastellaan ryhmää, joka koostuu 0:sta ja 1:stä binäärisen yhteenlaskun operaatiolla. Sen taulukko on:

Yksikkö 1 on selvästi oma käänteislukunsa. Tämäkin on abelinen ryhmä. Älä huoli, useimmat ryhmät eivät ole näin tylsiä.

Joitakin muita esimerkkejä ryhmistä ovat:

• Kokonaislukujen joukko yhteenlaskuineen.
• Rationaalilukujen joukko, joka ei sisällä 0:aa, kertolaskuineen.
• Polynomiyhtälön xⁿ-1=0 ratkaisujen joukko, jota kutsutaan n:nneksi ykkösen juuriksi, kertolaskuineen.

Tässä muutamia esimerkkejä, jotka eivät ole ryhmiä:

• Luonnollisten lukujen joukko yhteenlaskussa ei ole ryhmä, koska siinä ei ole käänteislukuja, joita olisivat negatiiviset luvut.
• Kaikkien rationaalilukujen joukko, mukaan lukien 0 kertolaskun kanssa, ei ole ryhmä, koska ei ole olemassa rationaalilukua q, jolle 0/q=1, joten jokaisella alkioyksiköllä ei ole käänteislukua.

Ryhmien rakenne

Ryhmä on paljon muutakin kuin pelkkä rykelmä, joka täyttää neljä aksioomaa. Ryhmällä voi olla sisäinen rakenne, ja tämä rakenne voi olla hyvin monimutkainen. Yksi abstraktin algebran perusongelmista on määritellä, miltä ryhmän sisäinen rakenne näyttää, sillä reaalimaailmassa ryhmät, joita todellisuudessa tutkitaan, ovat paljon suurempia ja monimutkaisempia kuin tässä annetut yksinkertaiset esimerkit.

Yksi sisäisen rakenteen perustyypeistä on alaryhmä. Ryhmällä G on alaryhmä H, kun H on G:n osajoukko ja:

• Jos a,b∈H, a*b∈H ja b*a∈H
• Jos a∈H, a-¹∈H
• Identiteetti on H:n alkio

Jos H≠G, niin H:n sanotaan olevan varsinainen aliryhmä. G:n alaryhmää, joka koostuu vain identiteetistä, sanotaan triviaaliseksi alaryhmäksi.

Eiabelilaisella ryhmällä voi olla kommutatiivisia alaryhmiä. Tarkastellaan neliönmuotoista dihedriryhmää, jota käsittelimme johdannossa. Tämä ryhmä ei ole abeelinen, mutta rotaatioiden alaryhmä on abeelinen ja syklinen:

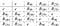
Annamme seuraavaksi kaksi esimerkkiä ryhmän rakenteesta.

Kun ryhmä G ei ole abelinen, voi silti olla niin, että on olemassa kokoelma G:n alkioita, jotka pendelöivät kaiken G:ssä olevan kanssa. Tätä kokoelmaa kutsutaan G:n keskukseksi. Keskus C on G:n alaryhmä. Todistus:

Asettakaamme nyt, että f on funktio, jonka alue ja kantama ovat molemmat G. F:n jakso on sellainen alkio a∈G, että f(x)=f(ax) kaikille x∈G. Joukko P f:n jaksoja on G:n alaryhmä. Todistus:

Finitit ryhmät ovat äärellisesti generoituja

Silmäilimme, että sykliset ryhmät generoituvat yhden alkion avulla. Kun on mahdollista kirjoittaa ryhmän G jokainen alkio G:n (ei välttämättä oikean) osajoukon A tuotteina, sanomme, että A generoi G:n ja kirjoitamme tämän muodossa G=⟨A⟩. Kaikkein ”noh, duh” -todistus, jonka tulet koskaan näkemään, on todistus siitä, että kaikki äärelliset ryhmät generoidaan äärellisellä generoivalla joukolla:

• Asettakaamme G:n olevan äärellinen. Jokainen G:n alkio on kahden muun G:n alkion tulo, joten G=⟨G⟩. QED.

Lopetamme tämän artikkelin sovellukseen.

Virheenkestävä tiedonsiirto

Yhden yksinkertaisimman tavan välittää digitaalista informaatiota koodaamalla se kiinteän pituisiksi binäärisarjoiksi. Mikään tiedonsiirtojärjestelmä ei ole täysin häiriötön, joten on aina olemassa mahdollisuus, että vastaanotetaan väärää tietoa. Suurimman todennäköisyyden dekoodausmenetelmä on yksinkertainen ja tehokas tapa havaita ja korjata siirtovirheitä.

Olkoon 𝔹ⁿ joukko binäärijonoja eli sanoja, joiden pituus on n. On suoraviivaista osoittaa, että 𝔹ⁿ on abeliaaninen ryhmä binäärisessä yhteenlaskussa ilman kantamista (jolloin esimerkiksi 010+011=001). Huomaa, että jokainen alkio on sen käänteisluku. Koodi C on 𝔹ⁿ:n osajoukko. Seuraavassa on esimerkki 𝔹⁶:

C = {000000, 001011, 010110, 011101, 100101, 101110, 110011, 111000}

Koodin elementtejä kutsutaan koodisanoiksi. Vain koodisanat lähetetään. Virheen sanotaan tapahtuvan, kun häiriö muuttaa lähetetyn sanan bittiä. Kahden koodisanan a ja b välinen etäisyys d(a,b) on niiden numeroiden lukumäärä, joissa kaksi koodisanaa eroaa toisistaan. Koodin minimietäisyys on pienin etäisyys kahden koodisanan välillä. Juuri edellä esitetyn esimerkkikoodin minimietäisyys on kolme.

Maksimimahdollisuuksien dekoodausmenetelmässä, jos vastaanotetaan sana x, joka voi sisältää virheitä, vastaanottajan tulisi tulkita x koodisanaksi a siten, että d(a,x) on minimi. Osoitan, että koodilla, jonka etäisyys on minimissään m, voidaan aina (1) havaita virheet, jotka muuttavat vähemmän kuin m bittiä, ja (2) korjata virheet, jotka muuttavat ½(m-1) tai vähemmän bittiä.

Esimerkkikoodissamme m=3 ja pallon säde ½(m-1)=1 koodisanan 011101 ympärillä on {011101, 111101, 001101, 011001, 010101, 011111, 011111}. Jos vastaanotin siis vastaanottaa minkä tahansa näistä sanoista, se tietää, että sen piti vastaanottaa 011101.

Se on siis ihan hyvä ja hyvä, mutta mitä tekemistä tällä on ryhmäteorian kanssa? Vastaus on siinä, miten me itse asiassa tuotamme koodit, joiden kanssa tämä menetelmä toimii.

On mahdollista, että 𝔹ⁿ:n koodi muodostaa alaryhmän. Tällöin sanomme, että koodi on ryhmäkoodi. Ryhmäkoodit ovat äärellisiä ryhmiä, joten ne ovat äärellisesti generoituja. Katsomme, miten koodin voi tuottaa löytämällä generoivan joukon.

Koodi voidaan määritellä siten, että jokaisen koodisanan ensimmäisiä bittejä kutsutaan informaatiobiteiksi ja lopussa olevia bittejä kutsutaan pariteettibiteiksi. Esimerkkikoodissamme C kolme ensimmäistä bittiä ovat informaatiobittejä ja kolme viimeistä ovat pariteettibittejä. Pariteettibitit täyttävät pariteettitarkistusyhtälöt. Koodisanalle A₁A₂A₃A₄A₅A₆ pariteettiyhtälöt ovat A₄=A₁+A₂, A₅=A₂+A₃ ja A₆=A₁+A₃. Pariteettiyhtälöt tarjoavat toisen kerroksen suojaa virheitä vastaan: jos jokin pariteettiyhtälöistä ei täyty, on tapahtunut virhe.

Tehdään näin. Oletetaan, että haluamme koodisanoja, joissa on m informaatiobittiä ja n pariteettibittiä. Ryhmäkoodin luomiseksi kirjoitetaan matriisi, jossa on m riviä ja m+n saraketta. Kirjoita ensimmäisten m sarakkeen muodostamaan lohkoon m×m-identiteettimatriisi. Kirjoita sarakkeeseen j, kun m+1≤j≤m_n, k:nteen riviin 1, jos Aₖ esiintyy pariteettibitin Aⱼ pariteettiyhtälössä, ja muutoin 0. Esimerkkikoodissamme matriisi on:

Tällaista matriisia kutsutaan ryhmäkoodin generointimatriisiksi. Voit suoraan todentaa, että rivit generoivat C:

Minkä tahansa generoivan matriisin rivit muodostavat ryhmäkoodin C generoivan joukon. Todistus:

• Identiteetti ja käänteisluku: Mikä tahansa rivi itseensä lisättynä antaa identiteetin, joka on kaikista nollista koostuva merkkijono.
• Sulku: Jos A,B∈C, niin A ja B ovat generoivan matriisin rivien summia, joten A+B on myös generoivan matriisin rivien summa. Siis A+B∈C.

Tämän avulla voimme generoida koodin, nyt näytän miten generoidaan käyttökelpoinen koodi.

Määritellään paino w(x) tarkoittamaan ykkösten lukumäärää x:ssä. Esimerkiksi w(100101)=3. On ilmeistä, että w(x)=d(x,0) missä 0 on sana, jonka kaikki numerot ovat nollia. Koodin minimipaino W on sen nollasta poikkeavan koodisanan paino, jolla on koodissa vähiten ykkösiä. Koodille, jonka minimietäisyys on m, d(x,0)≥m, joten w(x)≥m ja siten W=m.

Muistutetaan, että jotta sanaa voidaan pitää koodisanana, sen on täytettävä joukko pariteettitarkistusyhtälöitä. Esimerkkikoodissamme nämä ovat A₄=A₁+A₂, A₅=A₂+A₃ ja A₆=A₁+A₃. Voimme kirjoittaa nämä myös lineaarisena järjestelmänä:

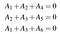
Joka puolestaan voidaan kirjoittaa pistetuotteina:

Vai kompaktimmassa muodossa: Ha=0 missä a=(A₁,A₂,A₃,A₄,A₅,A₆) ja H on koodin pariteettitarkistusmatriisi:

Voidaan todentaa suoralla laskutoimituksella, että jos w(a)≤2, niin silloin ei voi olla Ha=0. Yleensä minimipaino on t+1, missä t on pienin sellainen luku, että mikä tahansa H:n t:n sarakkeen kokoelma ei summaudu nollaan (ts. ne ovat lineaarisesti riippumattomia). Tämän todistaminen veisi meidät vain hieman liian pitkälle lineaarialgebraan.

Jos tämä pelottaa sinua, älä huoli. Voimme tuottaa erittäin hyviä koodeja ilman sitäkin hyödyntämällä sitä, että äsken mainitsemani tulos implikoi, että jos H:n jokainen sarake on nollasta poikkeava eikä mikään kaksi saraketta ole yhtä suuri, niin minimipaino, ja siten koodin minimietäisyys, on vähintään kolme. Tämä on erittäin hyvä: Jos viestintäjärjestelmässämme odotetaan olevan yksi bittivirhe jokaista sataa lähetettyä sanaa kohden, vain yhdessä kymmenestätuhannesta lähetetystä sanasta on korjaamaton virhe ja yhdessä miljoonasta lähetetystä sanasta on havaitsematta jäänyt virhe.

Tässä vaiheessa meillä on siis resepti, jolla voimme tuottaa käyttökelpoisen koodin suurimman todennäköisyyden havaitsemismenetelmää varten koodisanoille, jotka sisältävät m informaatio- ja n pariteettibittiä:

• Luo matriisin, jossa on m+n sarakkeita ja n riviä. Täytä matriisi ykkösillä ja nollilla niin, että yksikään sarake ei ole sama eikä yksikään sarake ole pelkkiä nollia.
• Tuloksena saadun pariteettitarkistusmatriisin jokainen rivi vastaa yhtä pariteettibitin yhtälöä. Kirjoita ne yhtälösysteemiksi ja ratkaise siten, että jokainen pariteettibitti kirjoitetaan informaatiobittien suhteen.
• Luo matriisi, jossa on m+n saraketta ja m riviä. Kirjoita ensimmäisten m sarakkeen muodostamaan lohkoon m×m-identiteettimatriisi. Kirjoita sarakkeeseen j, kun m+1≤j≤m_n, k:nteen riviin 1, jos Aₖ esiintyy pariteettibitin Aⱼ pariteettiyhtälössä, ja muutoin 0.
• Tämän matriisin rivit ovat sellaisen koodiryhmän generaattoreita, jonka minimietäisyys on vähintään kolme. Tätä koodia tulemme käyttämään.

Esimerkiksi oletetaan, että tarvitsen yksinkertaisen, kahdeksan sanan koodin ja tarvitsen vain jonkinlaista perusvirheentunnistusta enkä korjausta, joten voin selvitä minimietäisyydellä kaksi. Haluan kolme informaatiobittiä ja kaksi pariteettibittiä. Kirjoitan ylös seuraavan pariteettitarkistusmatriisin:

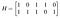
Tässä on kaksi parillista sarakeparia, jotka ovat yhtä suuria, joten pienin t, jolle mikä tahansa t:n sarakkeista koostuva kokoelma on lineaarisesti riippumaton, on yksi, joten minimipaino ja näin ollen minimietäisyyteni, jonka saan, on kaksi. Rivit edustavat pariteettitarkistusyhtälöitä A₄=A₁+A₃ ja A₅=A₁+A₂+A₃. Generointimatriisini on siis:

Ja tämän matriisin rivit generoivat koodiryhmän:

• {00000, 00111, 01001, 01110, 10011, 10100, 111010, 11101}

Loppuhuomautukset

Abstract algebra on syvällinen aihe, jolla on kauaskantoisia vaikutuksia, mutta se on myös hyvin helppo oppia. Lukuun ottamatta muutamia ohimeneviä mainintoja lineaarialgebrasta, lähes kaikki, mitä olen tässä käsitellyt, on helposti lähestyttävää sellaiselle, joka on käynyt vain lukion algebran.

Kun sain idean kirjoittaa tämän artikkelin, halusin oikeastaan puhua Rubikin kuutiosta, mutta lopulta halusin valita esimerkin, joka voitaisiin käsitellä vain ryhmäteorian perusideoilla. Lisäksi Rubikin kuution ryhmästä on niin paljon sanottavaa, että se ansaitsee itsenäisen artikkelin, joten se on tulossa pian.

Yliopistokurssini abstraktissa algebrassa perustuivat Charles Pinterin kirjaan A Book of Abstract Algebra, joka on helppokäyttöinen käsittely. Tässä artikkelissa olevat esimerkit on kaikki lainattu Pinterin kirjasta pienin muutoksin.

Loppuhuomautuksena: kaikki kuvat, joita ei ole mainittu, ovat omia alkuperäisiä töitäni, ja niitä saa käyttää mainiten. Kuten aina, otan mielelläni vastaan kaikki korjaukset tai selvennyspyynnöt.