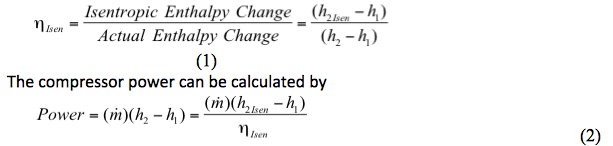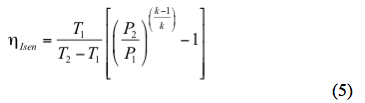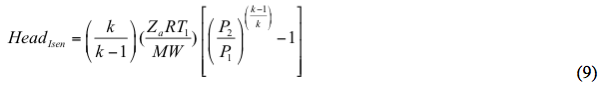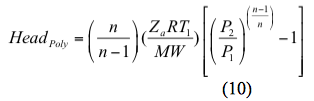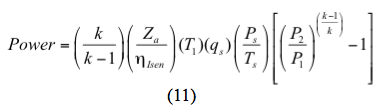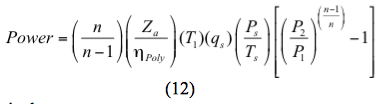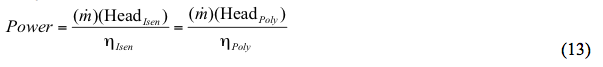Marraskuun 2011 kuukauden vinkissä (TOTM) esittelimme tapaustutkimuksen kompressorilaskelmia. Vertasimme tiukan menetelmän tuloksia oikotietomenetelmillä saatuihin arvoihin. Tiukka menetelmä perustui Soave-Redlich-Kwongin (SRK) kaltaiseen tilayhtälöön tarvittavien entalpioiden ja entropioiden laskemiseksi. Entalpioita ja entropioita käytetään tehontarpeen ja purkauslämpötilojen määrittämiseen. Tulokset osoittivat, että oikotietomenetelmän tarkkuus on herkkä ideaalikaasun olomuodon lämpökapasiteettisuhteen k arvolle.
Vain laskennan kannalta tehon laskenta on erityisen herkkä massavirran, imulämpötilan ja -paineen sekä poistolämpötilan ja -paineen määrittelylle. Kompressori toimii sen tehoon vaikuttavien muuttujien vaihtelevilla arvoilla. Näin ollen kompressorin laskennan vaikein osa on kunkin muuttujan kohtuullisen vaihteluvälin määrittäminen eikä itse laskenta. Viitteessä korostetaan, että yhden arvon käyttäminen kullekin muuttujalle ei ole oikea tapa arvioida kompressorijärjestelmää.
Normaalisti termodynaamiset laskelmat tehdään ideaaliselle (palautuvalle) prosessille. Palautuvan prosessin tulokset sovitetaan sitten reaalimaailmaan käyttämällä termodynaamista hyötysuhdetta. Puristusprosessissa on kolme ideaalista prosessia, jotka voidaan visualisoida: 1) isoterminen prosessi (PV1=C1), 2) isentrooppinen prosessi (PVk=C2) ja 3) polytrooppinen prosessi (PVn=C3). Mitä tahansa näistä prosesseista voidaan käyttää sopivasti perustana arvioitaessa puristustehon tarvetta joko käsin tai tietokoneella laskemalla. Isotermistä prosessia käytetään kuitenkin harvoin perusteena, koska normaalia teollista puristusprosessia ei suoriteta edes likimainkaan vakiolämpötilassa.
Huomaa, että Dresser Rand tekee melko paljon työtä ”Lähes vakiolämpötilassa” tapahtuvan puristuksen parissa, erityisesti hiilidioksidin puristamiseksi savukaasuputkista. Yksityiskohtaiset tiedot löytyvät osoitteesta:
Tässä TOTM:ssä esitellään, miten kompressorin hyötysuhde määritetään mitatusta virtausnopeudesta, koostumuksesta, imu- ja poistolämpötiloista ja -paineista. Tarkastellaan tiukkaa, tilanyhtälöön perustuvaa laskentaa ja oikotietomenetelmää, ja tuloksia verrataan keskenään.
Kompressorin hyötysuhde
Kompressorin hyötysuhde vaihtelee kompressorin tyypin, koon ja läpimenon mukaan. Ne voidaan määrittää (jälkikäteen) vain kompressoritestillä, vaikka kompressorivalmistajat voivat yleensä antaa hyviä arvioita. Suunnittelua varten suositellaan seuraavia kokonaishyötysuhteen arvoja:
Taulukko 1. Kompressorin kokonaishyötysuhde. Kompressorin kokonaishyötysuhteet
|
Kompressorityyppi |
Hyötysuhde, η |
||||||
|
Keskipakopakopakopakopakopakopakopakopakopakopakopakopakopakopakopakopakopakopakopakopakopaketit
Viittaus osoittaa, että nämä kokonaiseffienssit sisältävät kompressorin sisäisen kaasun kitkan, mekaaniset häviöt (laakerit, tiivisteet, vaihdelaatikko jne.) ja vaihdelaatikon tappiot. Mekaaninen hyötysuhde vaihtelee kompressorin koon ja tyypin mukaan, mutta 95 % on hyödyllinen suunnitteluluku. Kompressorin korkeutta ja ulostulolämpötilaa laskettaessa käytetään isentrooppista tai polytrooppista efficenssiä (isentrooppista efficenssiä kutsutaan joskus adiabaattiseksi efficenssiksi). Lisäämällä 3-4 % efficiency (mekaaniset häviöt) taulukossa 1 esitettyihin kokonaisefficienceihin saadaan yleensä hyvä arvio termodynaamisesta efficiency:stä. Olemassa olevan kompressorin suorituskyvyn arvioimiseksi tavoitteena on laskea kompressorin hyötysuhde (η) ja tehontarve. Tunnettuja ja mitattuja ominaisuuksia ovat: a. Vakiotilan kaasun tilavuusvirta (qS) tai kaasun massanopeus () b. Kaasun koostumus (zi) c. Imupaine (P1) ja lämpötila (T1) d. Poistopaine (P2) ja lämpötila (T2) Hyötysuhteen arviointi – tiukka menetelmä Kaiken kaupallisen prosessivirtauksen simulointiohjelmiston sydän on tilanyhtälö. Niiden yksinkertaisuuden ja suhteellisen tarkkuuden vuoksi käytetään kuutiomaista EOS:ää, kuten Soave Redlich-Kwong (SRK) tai Peng-Robinson. Näitä yhtälöitä käytetään höyry-neste-tasapainon (VLE), entalpian (h) ja entropian (s) laskemiseen. Oikeilla binäärisillä vuorovaikutuskertoimilla näiden kahden yhtälön prosessisimulointitulokset ovat käytännössä samat. Siksi tässä työssä käytetään vain SRK:ta. Isentrooppinen hyötysuhde määritellään
Jossa: ηIsen = Isentrooppinen hyötysuhde h1 = Imuentalpia, joka on laskettu P1:ssä, T1:ssä ja koostumuksessa (zi) h2 = Purkuentalpia, joka on laskettu P2:ssa, T2:ssa, ja koostumus (zi) h2Isen = Isentrooppinen purkautumisentalpia P2:ssa (tai T2:ssa), S2Isen =S1, ja koostumus (zi)
Kompressorin hyötysuhteen tai tehon laskemiseen kuuluu kaksi vaihetta 1. Kompressioprosessin ideaalisen tai isentrooppisen (reversiibelin ja adiabaattisen) entalpiamuutoksen (h2Isen-h1) määrittäminen. 2. Todellisen entalpiamuutoksen (h2-h1) määrittäminen. Vaiheittainen laskenta, joka perustuu EOS: a. Oletetaan vakaa tila, eli b. Oletetaan, että rehun koostumus pysyy muuttumattomana c. Laske imuentalpia h1=f(P1, T1 ja zi) ja entropia s1=f(P1, T1 ja zi) EOS:n avulla d. Oletetaan isentrooppinen prosessi ja asetetaan s2Isen = f (P2, T2Isen, zi) = s1 = f (P1, T1, zi). e. Laske ideaalinen entalpia (h2Isen) purkautumisolosuhteissa, kun zi, T2 (tai P2) ja s2Isen tunnetaan. f. Lasketaan todellinen entalpia (h2) purkautumisolosuhteissa tunnetuille zi, T2 ja P2. g. Lasketaan isentrooppinen hyötysuhde yhtälöllä 1: µIsen = (h2Isen – h1)/(h2 – h1) h. Lasketaan teho yhtälöllä 2: Hyötysuhteen arviointi – oikotiemenetelmä Isentrooppisen polun eksponentti (k) tai ideaalikaasun lämpökapasiteettisuhde (k=CP/CV) voidaan laskea toukokuun 2013 TOTM:ssä esitetyn korrelaation avulla:
Jossa: T = Lämpötila, K (°R)
A = 0.000272 (0.000151) Tosiasiallinen purkauslämpötila isentrooppisen reitin perusteella voidaan arvioida
Ratkaisemalla isentrooppinen hyötysuhde,
Samalla, polytrooppiseen polkuun perustuva todellinen purkauslämpötila voidaan arvioida
ratkaisemalla edellä oleva yhtälö polytrooppisen polun kertoimelle (n):
Vastaavasti polytrooppiseen polkuun perustuva todellinen purkautumislämpötila voidaan arvioida (ηPoly) seuraavasti:
Isentrooppinen korkeus lasketaan seuraavasti:
Vastaavasti, polytrooppinen pää lasketaan
Isentrooppiselle (palautuvalle ja adiabaattiselle) prosessille teho lasketaan
tai polytrooppiselle prosessille teho lasketaan
Vaihtoehtoisesti:
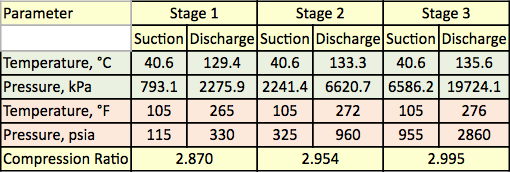
Missä: Korkeus = Kompressorin korkeus, m (ft) Teho = Kompressorin teho, kW (HP) R = Yleiskaasuvakio, 848 kg-m/(kmol-K) tai (1545 ft-lbf/(lbmol-°R)) PS = Vakiotilapaine, kPa (psia) P1 = Imupaine, kPa (psia) P2 = Poistopaine, kPa (psia) TS = Vakiolämpötila, K (°R) T1 = Imulämpötila, K (°R) T2 = Poistolämpötila, K (°R) qS = Kaasun tilavuusvirta vakiotilanteessa, Sm3/d (scf/vrk) Za = Kaasun keskimääräinen kokoonpuristuvuuskerroin = (Z1+Z2)/2 Z1 = Kaasun kokoonpuristuvuuskerroin imutilanteessa Z2 = Kaasun kokoonpuristuvuuskerroin purkautumistilanteessa MW = Kaasun molekyylipaino Teholaskenta on tehtävä kompressiovaihetta kohti ja sen jälkeen laskettava yhteen kaikkien yhteen ajuriin kytkettyjen vaiheittain. Vaiheittainen laskenta oikotiemenetelmää varten a. Lasketaan isentrooppinen eksponentti (k) yhtälöllä 3 käyttäen keskilämpötilaa, joka määritellään kaavalla T = (T1+3T2)/4. Tämä keskilämpötilan muoto määriteltiin, jotta tiukan ja oikotietomenetelmän tulokset vastaisivat paremmin toisiaan. b. Lasketaan isentrooppinen hyötysuhde (ηIsen) yhtälöllä 5. c. Lasketaan polytrooppinen kerroin (n) yhtälöllä 7. d. Lasketaan polytrooppinen hyötysuhde (ηPoly) yhtälöllä 8. e. Lasketaan isentrooppinen ja polytrooppinen pää yhtälöiden 9 ja 10 avulla. f. Lasketaan tarvittava teho vaihetta kohti joko yhtälöllä 11 tai 12. Tapaustutkimus Maakaasuseosta puristetaan kolmivaiheisella keskipakokompressorilla. Prosessin virtauskaavio on esitetty kuvassa 1. Kunkin vaiheen mitatut paineet ja lämpötilat esitetään taulukossa 1. Mitattu syötteen koostumus, virtausnopeudet sekä laskettu molekyylipaino ja suhteellinen tiheys esitetään taulukossa 2. 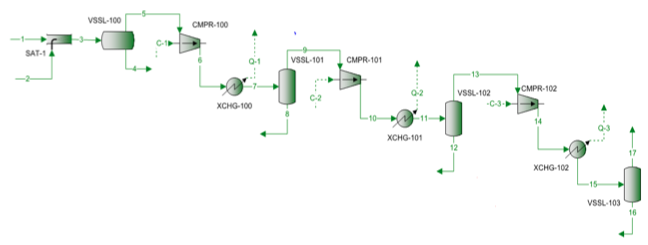
Kuva 1. Prosessin virtauskaavio kolmivaiheista puristusta varten Taulukko 1. Mitattu lämpötila ja paine kolmessa kompressiovaiheessa
Taulukko 2. Kaasuanalyysi ja virtausnopeus kolmessa puristusvaiheessa 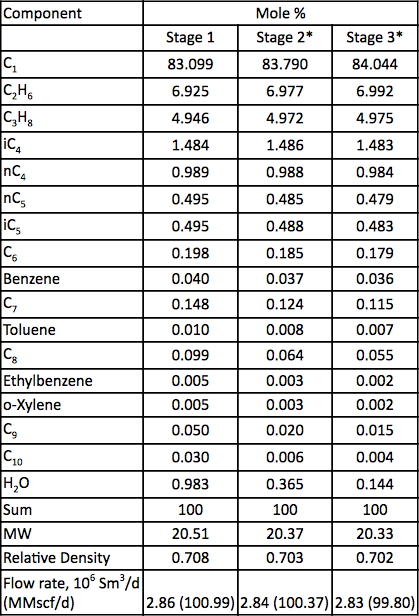
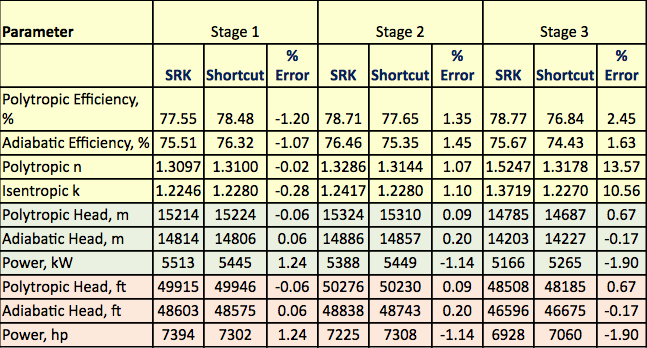
* Laskennallinen Tulokset ja keskustelut Kuvassa 1 esitetty prosessin virtauskaavio simuloitiin ProMax-ohjelmistolla tiukkojen laskelmien suorittamiseksi SRK:n EOS:n avulla. Ohjelma laski polytrooppiset ja isentrooppiset hyötysuhteet, syöttökorkeudet ja puristustehon. Ohjelma laski myös isentrooppisen polun eksponentin (k) ja polytrooppisen polun eksponentin (n). Nämä lasketut tulokset esitetään taulukossa 2 kaikkien kolmen vaiheen osalta SRK-otsakkeilla. ProMaxin suorittamat laskelmat ovat hyvin samankaltaisia kuin tiukassa jaksossa kuvatut vaiheittaiset a-h-laskelmat. Taulukossa 2 esitetään myös oikotien laskentatulokset vastaaville arvoille oikotien otsikon alla. Oikolaskennat perustuvat oikolaskentamenetelmää koskevassa jaksossa kuvattuihin vaihe vaiheelta a-f tehtäviin laskelmiin. Taulukossa 2 esitetään myös virheprosentit tiukan menetelmän ja oikotien menetelmien välillä kunkin vaiheen osalta. Taulukosta 2 käy ilmi, että vaiheiden 1 ja 2 osalta saavutetaan erinomaiset sopimukset. Vaiheen 3 isetrooppisten ja polytrooppisten eksponenttien osalta havaitaan kuitenkin suurempia poikkeamia, jotka johtuvat korkean paineen toiminnasta, joka poikkesi liian kauas ideaalisesta kaasutilasta. Taulukko 3. Yhteenveto tiukan ja oikolaskennan lasketuista tuloksista
Johtopäätökset Taulukosta 2 käy ilmi, että oikolaskennan ja tiukan laskennan tulosten välillä on hyvät sopimukset. Erot tiukan ja lyhyen menetelmän tulosten välillä tilojen laskennassa ja suunnittelussa ovat vähäisiä. Vaiheessa 3 havaitaan isentrooppisen eksponentin (k) osalta suurempi virhe, joka johtuu korkeapaineisesta toiminnasta ja liian suuresta poikkeamasta ihanteellisesta kaasutilaolosuhteesta. ProMaxissa laskettu isentrooppinen eksponentti (k) ei ole ihanteellisen kaasutilan lämpökapasiteetin (CP/CV) suhde. Se on se isentrooppisen eksponentin arvo, joka tarvitaan, jotta saadaan aikaan isentrooppinen reitti sisääntulosta ulostuloon. Sen arvo lasketaan integroimalla kyseinen reitti. Näin ollen se on jonkinlainen ”keskiarvo”, joka edustaa todellista isentrooppista reittiä. Ihanteellisille kaasuille arvo olisi yhtä suuri kuin (CP/CV)-suhde. Tämä ”k”-virhe havainnollistaa myös sen, kuinka tärkeää on määritellä, mitä korrelaatiota käytetään suorituskykytestiä tilattaessa (ts. katso ASME PTC-10 -standardi lisätietojen saamiseksi), niin että asiakas ja toimittaja ovat samassa yhteisymmärryksessä testinesteen molekyylipainon (MW) ja k:n suhteen. Lisätietoja on viitteessä ja elokuun ja syyskuun 2010 TOTM:ssä . Voi myös olla syytä huomata, että kun n-arvoa ja polytrooppista hyötysuhdetta arvioidaan koneen kunnon arvioimiseksi, mittauslaitteiden ja -välineiden (lämpötila- ja paineanturit) suhteellinen tarkkuus ja kompressorin suorituskyvyn kuvaaminen alkuperäiseen suorituskykykäyrään (todellisen kaasun tilavuusvirran ja kierrosluvun suhde nopeuden välille) tuovat monia potentiaalisia virhelähteitä mukaan tähän päivittäiseen arviointiin. Huomaa, että oikotiemenetelmien tarkkuus riippuu k:n ja n:n arvoista. Keskilämpötilan määritelmää oikotiemenetelmässä mukautettiin, jotta tiukalla menetelmällä laskettu isentrooppisen polun eksponentti (k) vastaisi paremmin. Jos haluat oppia lisää vastaavista tapauksista ja käyttöongelmien minimoimisesta, suosittelemme osallistumaan kursseillemme G4 (Kaasun ilmastointi ja käsittely), PF4 (Öljyntuotanto- ja jalostuslaitokset), ME46 (Kompressorijärjestelmät-mekaaninen suunnittelu ja spesifikaatiot) ja ME44 (Pumppu- ja kompressorijärjestelmien perusteet). PetroSkills tarjoaa konsultointiasiantuntemusta tästä ja monista muistakin aiheista. Lisätietoja näistä palveluista saat verkkosivuiltamme osoitteesta http://petroskills.com/consulting tai sähköpostitse osoitteesta [email protected]. Tohtori Mahmood Moshfeghian Viitteet: 3. Soave, G., Chem. Eng. Sci., Vol. 27, s. 1197-1203, 1972. 4. Peng, D. Y., ja Robinson, D. B., Ind. Eng. Chem. Fundam., Vol. 15, s. 59, 1976. 5. ProMax 3.2, Bryan Research and Engineering, Inc, Bryan, Texas, 2014. 6. ASME PTC-10, ”Performance test Code on Compressors and Exhausters”, 1997. 7. Honeywell, J. ”Keskipakokompressorien testauksen tärkeät näkökohdat – osa 1”, Kuukauden vinkki, elokuu 2010 8. Honeywell, J. ”Keskipakokompressorien testauksen tärkeät näkökohdat – osa 2”, Kuukauden vinkki, syyskuu 2010 . |