Eigenarvot ovat erityinen joukko skalaareja, jotka liittyvät lineaariseen yhtälösysteemiin (i.e., matriisiyhtälöön), jotka tunnetaan joskus myös nimillä ominaisjuuret, ominaisarvot (Hoffman ja Kunze 1971), itseisarvot tai latentit juuret (Marcus ja Minc 1988, s. 144).

Systeemin ominaisarvojen ja ominaisvektoreiden määrittäminen on erittäin tärkeää fysiikassa ja tekniikassa, jossa se vastaa matriisien diagonalisointia, ja se nousee esiin sellaisissa tavallisissa sovelluksissa kuten stabiilisuusanalyysissä, pyörivien kappaleiden fysiikassa ja värähtelevien systeemien pienissä oskilloinneissa, vain muutamia mainitakseni. Jokaisella ominaisarvolla on vastaava niin sanottu ominaisvektori (tai yleensä vastaava oikea ominaisvektori ja vastaava vasen ominaisvektori; vasemman ja oikean välillä ei ole vastaavaa erottelua ominaisarvojen osalta).

Neliönmuotoisen matriisin hajottaminen ominaissuureiksi ja omavektoreiksi tunnetaan tässä työssä nimellä ominaissuureiden hajottaminen, ja se, että tämä hajottaminen on aina mahdollista niin kauan kuin matriisin omavektoreista koostuva matriisi on neliönmuotoinen, tunnetaan nimellä ominaissuureiden hajottamisen teoreema.

Lanczosin algoritmi on algoritmi suurten symmetristen harvalukuisten matriisien ominaisarvojen ja -vektoreiden laskemiseen.

Olkoon lineaarinen muunnos, jota esittää matriisi . Jos on olemassa vektori siten, että

(1)

jollekin skalaarille , niin kutsutaan :n :n ominaissuureksi, jolla on vastaava (oikea) ominaissuure .

Olkoon neliömatriisi

(2)

, jolla on ominaissuure , niin vastaavat ominaisvektorit täyttävät

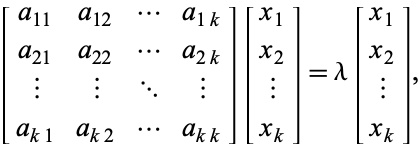(3)

, mikä vastaa homogeenista systeemiä

.

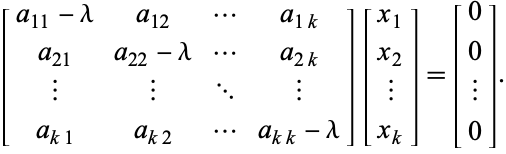(4)

Yhtälö (4) voidaan kirjoittaa kompaktisti muotoon

(5)

jossa on identtisyysmatriisi. Kuten Cramerin säännöstä käy ilmi, lineaarisella yhtälösysteemillä on ei-triviaaleja ratkaisuja, jos determinantti häviää, joten yhtälön (5) ratkaisut saadaan

(6)

Tämä yhtälö tunnetaan :n karakteristisena yhtälönä, ja vasemmanpuoleinen puoli tunnetaan karakteristisena polynomina.

Esimerkiksi -matriisille, ominaisarvot ovat

(7)

jotka syntyvät ratkaisuna yhtälön characteristicequation

(8)

Jos kaikki ominaisarvot ovat erilaisia, niin liittämällä nämä takaisin, saadaan riippumatonta yhtälöä kunkin vastaavan ominaisvektorin komponentille, ja systeemin sanotaan olevan degeneroitumaton. Jos ominaisarvot ovat -kertaisesti degeneroituneet, systeemin sanotaan olevan degeneroitunut ja ominaisvektorit eivät ole lineaarisesti riippumattomia. Tällöin voidaan soveltaa lisärajoitusta, jonka mukaan ominaisvektorit ovat ortogonaalisia,

(9)

jossa on Kroneckerin delta, jolloin saadaan lisärajoituksia, jotka mahdollistavat ratkaisun ominaisvektoreille.

Eigenarvot voidaan laskea Wolfram-kielessä käyttämällä ominaisarvoja. Omavektorit ja ominaisarvot voidaan palauttaa yhdessä komennolla Eigensystem.

Asettakaamme, että tiedämme

(10)

Lisäämällä vakio kertaa identiteettimatriisi :een,

(11)

siten uudet itseisarvot ovat yhtä suuret kuin vanhat plus . Kertomalla vakiolla

(12)

siten uudet ominaissuureet ovat vanhat kerrottuna :llä.

Käsitellään nyt samankaltaisuustransformaatio, jossa on muunnos . Olkoon :n determinantti, niin

			(13)
			(14)
			(15)

siten ominaissuureet ovat samat kuin :lle.