Käyttääksesi suorakulmalaskinta yksinkertaisesti syötä suorakulmaisen kolmion minkä tahansa kahden sivun pituudet ylimpiin ruutuihin. Laskin määrittää sitten jäljelle jäävän sivun pituuden, kolmion pinta-alan ja ympärysmitan sekä kaikki kolmion kulmat.

Miten löytää suorakulmaisen kolmion pinta-ala ja sivut

Tee se itse

Jos tiedämme suorakulmaisen kolmion vain kaksi sivua, voimme käyttää näitä tietoja löytääksemme kolmion kolmannen sivun, pinta-alan ja ympärysmitan sekä kaikki kolmion kulmat. Hämmästyttävää, eikö? Käydään vielä läpi, miten löytäisimme jokaisen näistä osista.

Miten löydämme suorakulmaisen kolmion puuttuvan sivun

Suorakulmaisen kolmion puuttuvan sivun löytämiseksi käytämme kuuluisaa Pythagoraan lausetta.

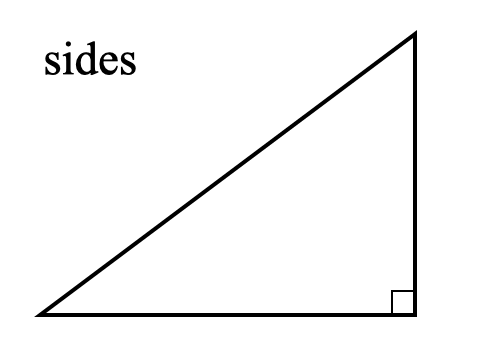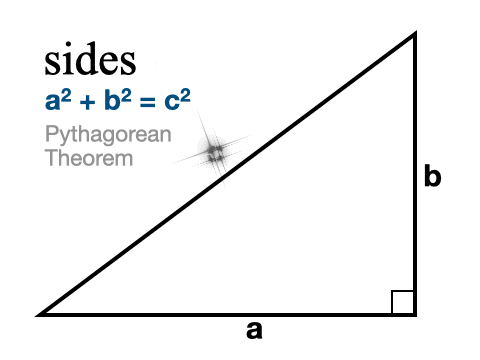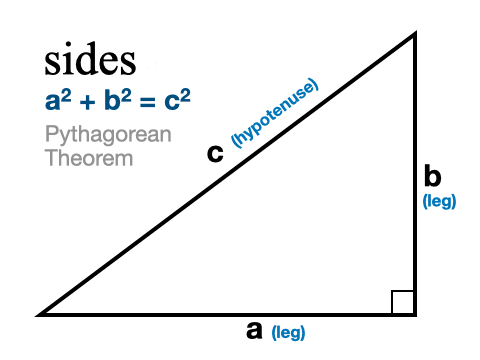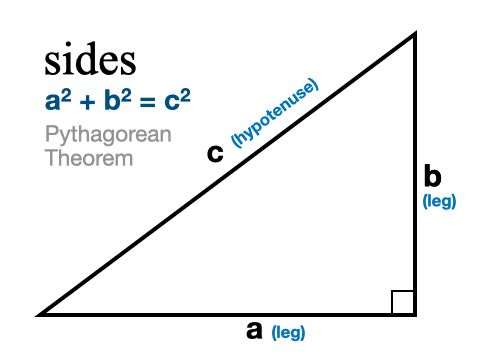
Meidän on oltava hieman varovaisia sen suhteen, että tiedämme, mitä sivua olemme löytämässä. Suorakulmaisilla kolmioilla on kaksi jalkaa ja hypotenuusa, joka on pisin sivu ja joka on aina oikean kulman poikki. Kun yritämme löytää hypotenuusan, korvaamme kaksi tuntemaamme sivua a:lla ja b:llä. Sillä ei ole väliä, kumpi jalka on a ja kumpi b. Sitten ratkaisemme c:n laskemalla yhteen a:n ja b:n neliöarvot ja ottamalla neliöjuuren molemmista sivuista.

Kun yritämme löytää jommankumman jalan, kirjoitamme tunnetun jalan a:ksi ja tunnetun hypotenuusan c:ksi. Sitten ratkaisemme b:n käyttämällä yksinkertaista algebraa (vähennämme molemmista sivuista a:n neliöarvon ja otamme sitten neliöjuuren molemmista sivuista).

Miten löydetään suorakulmaisen kolmion pinta-ala

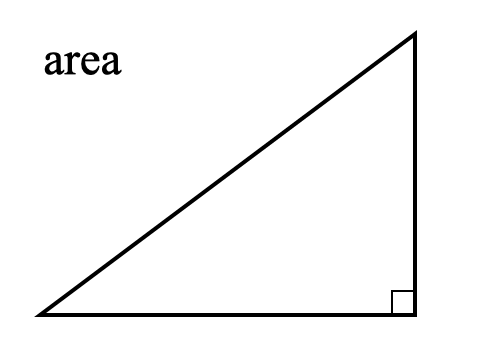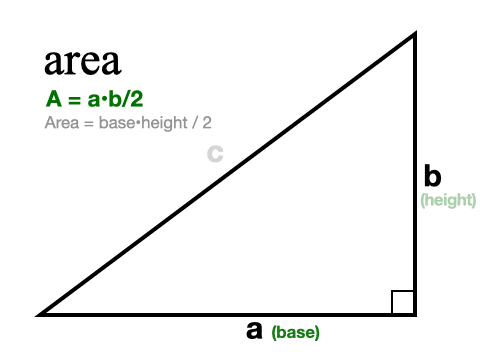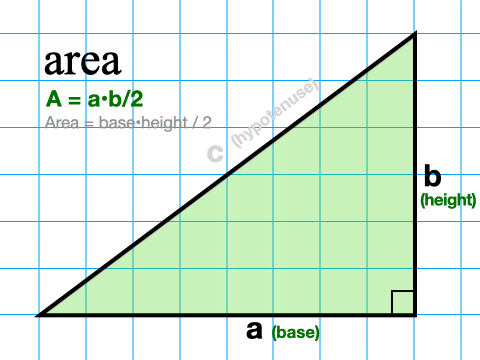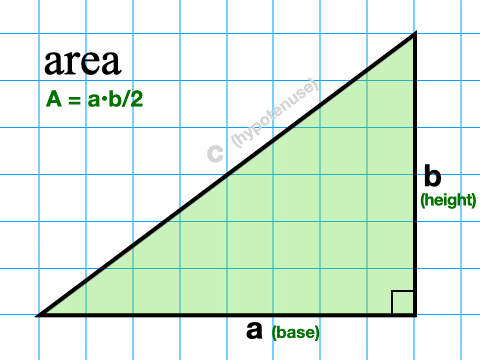
Suorakulmaisen kolmion pinta-alan löytämiseksi meidän tarvitsee tietää vain kahden jalan pituus. Emme tarvitse hypotenuusaa lainkaan. Tämä johtuu siitä, että jalat määrittävät kolmion pohjan ja korkeuden jokaisessa suorakulmaisessa kolmiossa. Käytämme siis yleistä kolmion pinta-alan kaavaa (A = pohja – korkeus/2) ja korvaamme pohjan ja korkeuden a:lla ja b:llä. Uusi suorakulmaisen kolmion pinta-alan kaava on siis A = ab/2.

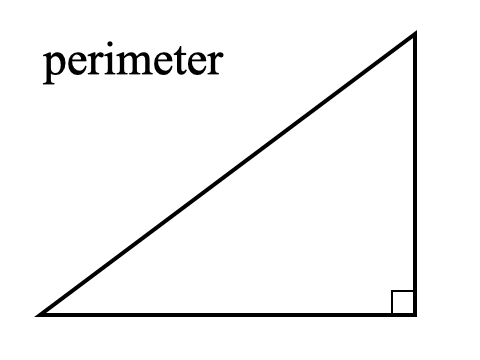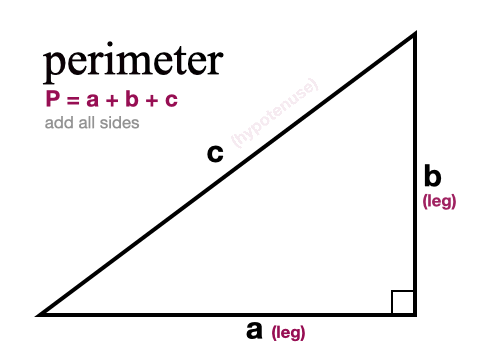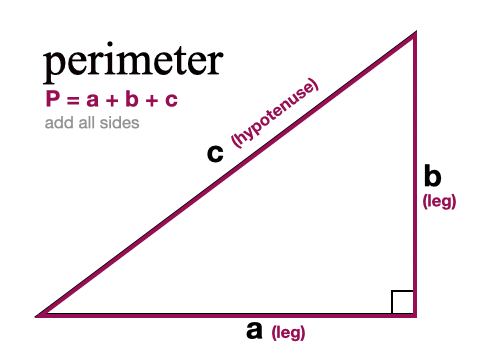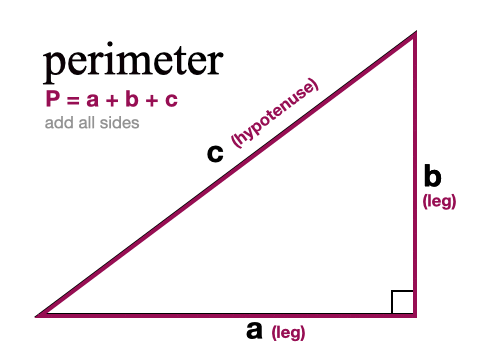
Miten löydetään suorakulmaisen kolmion ympärysmitta

Löytääksemme kolmiomme ympärysmitan eli kolmiota ympäröivän etäisyyden meidän on yksinkertaisesti laskettava kaikki kolme sivua yhteen. Jos tiedämme vain kaksi sivua, meidän on ensin käytettävä Pythagoraan lausetta kolmannen sivun löytämiseksi.

Miten löydetään suorakulmaisen kolmion kulmat

Suorakulmaisen kolmion kulmien löytämiseksi käytämme trigonometriaa. Se ei ole niin vaikeaa kuin miltä se kuulostaa. Meidän on vain löydettävä yksi erityinen painike kämmenlaskimistamme. Aluksi meidän on tiedettävä kaikki sivujen pituudet, joten jos emme vielä tiedä niitä, käytämme ensin Pythagoraan lausetta niiden löytämiseen.

Kun meillä on kaikki sivut tiedossa, määrittelemme, minkä kulman aiomme löytää. Sitten otamme tätä kulmaa vastapäätä olevan sivun ja jaamme sen hypotenuusan pituudella, joka on sivu c. Näin saamme arvon väliltä 0 ja 1. Nyt meidän on vain löydettävä laskimestamme ARCSIN-painike, joka on usein merkitty nimellä SIN-1. Kun löydämme desimaaliarvomme ARCSINin, saamme kulmamme. Varmista, että laskin on asetettu kulmatilaan eikä radiaanitilaan.

Voimme toistaa tämän prosessin löytääksemme kolmion toisen tuntemattoman kulman jakamalla jälleen kerran sen vastakkaisen sivun hypotenuusalla ja ottamalla sitten ARCSIN.

Vai voimmeko osoittaa vielä enemmän kolmiotietämystä käyttämällä vähennyslaskutoimitusta sen löytämiseksi, koska tiedämme, että kolmion sisäkulmien on summauduttava 180°:ksi. Kun vähennämme juuri löytämämme kulman 180°:sta ja sitten vähennämme tuntemamme suoran kulman (90°), saamme myös kolmannen kulman.

Tämä laskin on loistava saadaksemme kaikki nämä tiedot vain suorakulmaisen kolmion kahdesta sivusta, mutta on hauska haaste yrittää löytää sivut, kulmat, pinta-ala ja ympärysmitta itse ilman sitä. Sitten voit käyttää sitä vastaustemme tarkistamiseen.