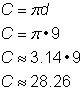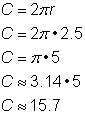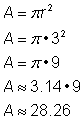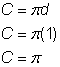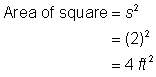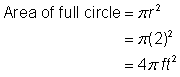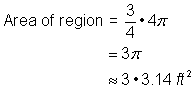Ympyrät
Oppimistavoite(t)
– Tunnistaa ympyrän ominaisuuksia.
– Löytää ympyrän kehä.
– Löytää ympyrän pinta-ala.
– Löytää koostettujen geometristen kuvioiden pinta-ala ja ympärysmitta.
Esittely
Ympyrät ovat yleinen muoto. Niitä näkee kaikkialla – auton pyörät, ilmassa kulkevat frisbeet, tietoja välittävät CD-levyt. Nämä kaikki ovat ympyröitä.
Ympyrä on kaksiulotteinen hahmo aivan kuten monikulmio ja nelikulmio. Ympyrät mitataan kuitenkin eri tavalla kuin nämä muut muodot – niiden kuvaamiseen on jopa käytettävä joitakin eri termejä. Tutustutaanpa tähän mielenkiintoiseen muotoon.
Ympyrän ominaisuudet
Ympyrä edustaa joukkoa pisteitä, jotka kaikki ovat saman etäisyyden päässä kiinteästä keskipisteestä. Tätä kiinteää pistettä kutsutaan keskipisteeksi. Etäisyyttä ympyrän keskipisteestä mihin tahansa ympyrän pisteeseen kutsutaan säteeksi.
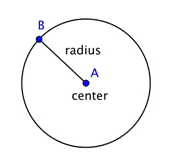
Kun kaksi sädettä (säteen monikko) yhdistetään muodostaen ympyrän poikki kulkeva viivasegmentti, saadaan halkaisija. Ympyrän halkaisija kulkee ympyrän keskipisteen kautta ja sen päätepisteet ovat itse ympyrällä.
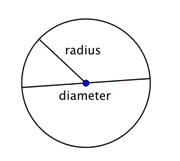
Minkä tahansa ympyrän halkaisija on kaksi kertaa kyseisen ympyrän säteen pituus. Se voidaan esittää lausekkeella 2r eli ”kaksi kertaa säde”. Jos siis tiedät ympyrän säteen, voit kertoa sen kahdella löytääksesi halkaisijan; tämä tarkoittaa myös sitä, että jos tiedät ympyrän halkaisijan, voit jakaa sen kahdella löytääksesi säteen.
|
Esimerkki |
||
|
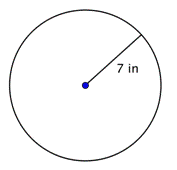
Obgelma |
Löydä ympyrän halkaisija.
|
|
|
d = 2r d = 2(7) d = 14 |
Ympyrän läpimitta on kaksi kertaa säde eli 2r. Tämän ympyrän säde on 7 tuumaa, joten halkaisija on 2(7) = 14 tuumaa. |
|
|
Vastaus |
Halkaisija on 14 tuumaa. |
|
|
Esimerkki |
||
|
Tehtävä |
||
|
Esimerkki |
||
|
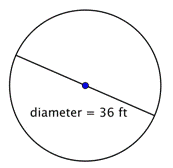
Löydetään ympyrän säde.
|
||
|
|
Ympyrän säde on puolet halkaisijasta eli |
|
|
Vastaus |
Säde on 18 jalkaa. |
|
Ympärysmitta
Ympyrän ympärillä olevaa matkaa kutsutaan kehäksi. (Muistetaan, että monikulmion ympärysmitta on kehä.)
Ympyröiden yksi mielenkiintoinen ominaisuus on, että ympyrän kehän ja halkaisijan suhde on sama kaikilla ympyröillä. Ympyrän koosta riippumatta ympyrän ympärysmitan ja halkaisijan suhde on sama.
Alhaalla on esitetty muutamia todellisia mittoja eri kappaleista. Mitat ovat tarkkoja millimetrin tai neljänneksen tuuman tarkkuudella (riippuen käytetystä mittayksiköstä). Katso kunkin kappaleen ympärysmitan ja halkaisijan suhdetta – vaikka kappaleet ovat erilaisia, suhde on jokaisella kappaleella suunnilleen sama.
|
Kappale |
Ympärysmitta (C) (pyöristettynä lähimpään sadasosaan) |
Halkaisija (d) |
Suhde |
|
Kuppi |
253 mm |
79 mm |
|
|
Neljännes |
8484 mm |
27 mm |
|
|
Kulho |
37.25 in |
11.75 in |
|
Ympärysmitta ja halkaisija ovat suuntaa-antavia mittoja, sillä tarkkaa tapaa näiden mittojen täsmälliseen mittaamiseen ei ole. Jos pystyisit kuitenkin mittaamaan ne tarkemmin, havaitsisit, että suhde ![]() siirtyisi kohti 3,14:ää kunkin annetun kohteen osalta. Suhteen
siirtyisi kohti 3,14:ää kunkin annetun kohteen osalta. Suhteen ![]() matemaattinen nimi on pi, ja se esitetään kreikkalaisella kirjaimella
matemaattinen nimi on pi, ja se esitetään kreikkalaisella kirjaimella ![]() .
.
![]() on päättymätön ja toistumaton desimaaliluku, joten sitä on mahdotonta kirjoittaa kokonaan.
on päättymätön ja toistumaton desimaaliluku, joten sitä on mahdotonta kirjoittaa kokonaan. ![]() :n 10 ensimmäistä numeroa ovat 3,141592653; se pyöristetään usein 3,14:ään tai arvioidaan murtolukuna
:n 10 ensimmäistä numeroa ovat 3,141592653; se pyöristetään usein 3,14:ään tai arvioidaan murtolukuna ![]() . Huomaa, että sekä 3,14 että
. Huomaa, että sekä 3,14 että ![]() ovat
ovat ![]() :n approksimaatioita, ja niitä käytetään laskutoimituksissa, joissa ei ole tärkeää olla tarkka.
:n approksimaatioita, ja niitä käytetään laskutoimituksissa, joissa ei ole tärkeää olla tarkka.
Koska tiedät, että ympärysmitan ja halkaisijan suhde (tai ![]() ) on yhdenmukainen kaikilla ympyröillä, voit käyttää tätä lukua ympyrän ympärysmitan selvittämiseen, jos tiedät sen halkaisijan.
) on yhdenmukainen kaikilla ympyröillä, voit käyttää tätä lukua ympyrän ympärysmitan selvittämiseen, jos tiedät sen halkaisijan.
![]() =
= ![]() , joten C =
, joten C = ![]() d
d
Mutta koska d = 2r, niin C = ![]() d =
d = ![]() (2r) = 2
(2r) = 2![]() r.
r.
Ympyrän ympärysmitta
Ympyrän ympärysmitan (C) löytämiseksi käytetään yhtä seuraavista kaavoista:
Jos tiedät ympyrän halkaisijan (d): ![]()
Jos tiedät ympyrän säteen (r): ![]()
|
Esimerkki |
||
|
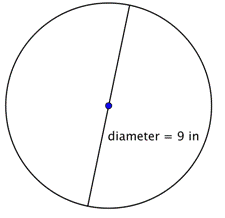
Tehtävä |
Löydä ympyrän kehä.
|
|
|
|
Lasketaan ympyrän ympärysmitta, kun halkaisija on 9 tuumaa, kaavalla Koska käytät likiarvoa arvolle |
|
|
Vastaus |
Ympärysmitta on 9 |
|
|
Esimerkki |
||
|
Tehtävä |
Löydä ympyrän ympyrän kehä, jonka säde on 2.5 jaardia. |
|
|
|
Lasketaan ympyrän ympärysmitta, jonka säde on 2,5 jaardia, kaavalla |
|
|
Vastaus |
Ympyrän ympärysmitta on 5 |
|
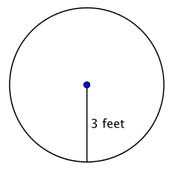
Ympyrän säde on 8 tuumaa. Mikä on sen kehä pyöristettynä lähimpään tuumaan?
A) 25 tuumaa
B) 50 tuumaa
C) 64 tuumaa2
D) 201 tuumaa
Pinta-ala
![]() on tärkeä luku geometriassa. Olet jo käyttänyt sitä ympyrän kehän laskemiseen. Käytät
on tärkeä luku geometriassa. Olet jo käyttänyt sitä ympyrän kehän laskemiseen. Käytät ![]() myös silloin, kun lasket ympyrän pinta-alaa.
myös silloin, kun lasket ympyrän pinta-alaa.
Ympyrän pinta-ala
Ympyrän pinta-alan (A) löytämiseksi käytä kaavaa: ![]()
|
Esimerkki |
||
|
Tehtävä |
Löydä ympyrän ala.
|
|
|
|
Tämän ympyrän pinta-alan selvittämiseksi käytä kaavaa Muista kirjoittaa vastaus neliöyksikköinä, koska olet löytämässä pinta-alaa. |
|
|
Vastaus |
Pinta-ala on 9 |
|
Napin halkaisija on 20 millimetriä. Mikä on napin pinta-ala? Käytä approksimaationa 3,14 ![]() .
.
A) 62,8 mm
B) 314 mm2
C) 400 mm2
D) 1256 mm2
Ympyrän kehä ja pinta-ala
Nyt kun osaat laskea ympyrän ympärysmitan ja pinta-alan, voit käyttää tätä tietämystä apunasi, kun haluat löytää ympyrän kehän ja pinta-alan. Temppu tämäntyyppisten ongelmien ratkaisemisessa on tunnistaa yhdistetyn kuvion sisällä olevat muodot (ja muotojen osat), laskea niiden yksittäiset mitat ja laskea ne sitten yhteen.
Katso esimerkiksi alla olevaa kuvaa. Onko mahdollista löytää ympärysmitta?
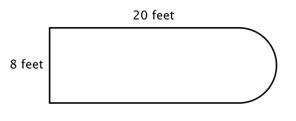
Ensimmäinen askel on tunnistaa yksinkertaisemmat hahmot tämän yhdistetyn kuvion sisällä. Voit jakaa sen suorakulmioon ja puoliympyrään, kuten alla on esitetty.
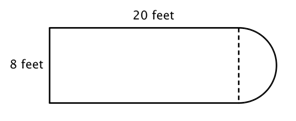
Voit löytää suorakulmion kehän ja ympyrän kehän. Tässä suorakulmion kolmen kiinteän sivun ympärysmitta on 8 + 20 + 20 = 48 jalkaa. (Huomaa, että vain suorakulmion kolme sivua summautuu yhdistetyn kuvion ympärysmittaan, koska toinen sivu ei ole reunalla, vaan puoliympyrä peittää sen!)
Puoliympyrän ympärysmitan selvittämiseksi käytä kaavaa ![]() halkaisijaltaan kahdeksan jalan suuruisen ympyrän halkaisijan ollessa kahdeksan jalkaa ja ota sitten puolet tuloksesta. Puoliympyrän kehä on
halkaisijaltaan kahdeksan jalan suuruisen ympyrän halkaisijan ollessa kahdeksan jalkaa ja ota sitten puolet tuloksesta. Puoliympyrän kehä on ![]() eli noin 12,56 jalkaa, joten kokonaisympyrä on noin 60,56 jalkaa.
eli noin 12,56 jalkaa, joten kokonaisympyrä on noin 60,56 jalkaa.
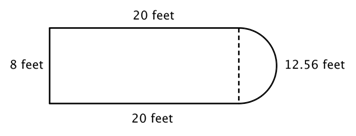
|
Esimerkki |
||
|
Tehtävä |
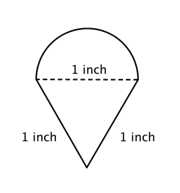
Erittäkää puoliympyrän ja kolmion muodostaman yhdistetyn kuvion ympärysmitta (sadasosan tarkkuudella).
|
|
|
|
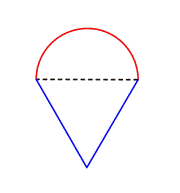
Tunnista pienemmät muodot yhdistetyn kuvion sisällä. Tämä kuvio sisältää puoliympyrän ja kolmion. |
|
|
Halkaisija (d) = 1
Puoliympyrän ympärysmitta = |
Löydä ympyrän kehä. Jaa sitten kahdella löytääksesi puoliympyrän kehän. |
|
|
|
|
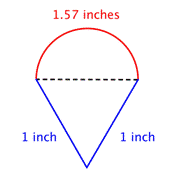
Löydä kokonaisympyräpiiri laskemalla yhteen puoliympyrän ympyräpiirin ympärysmitta ja molempien jalkojen pituudet. Koska mittaamamme puoliympyrän ympärysmitta on likimääräinen, myös ympärysmitta on likimääräinen. |
|
Vastaus |
Lähes 3.57 tuumaa |
|
|
Esimerkki |
||
|
Tehtävä |
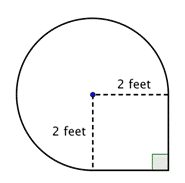
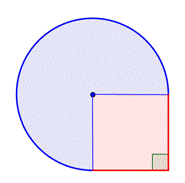
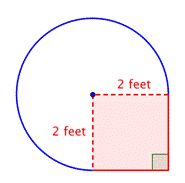
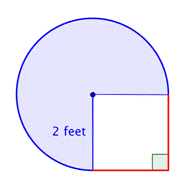
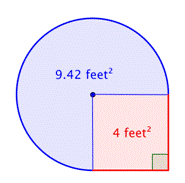
Erittäkää yhdistelmäkuvion ala, joka muodostuu kolmen neljäsosan ympyrästä ja neliöstä, lähimmän sadasosan tarkkuudella.
|
|
|
|
Tunnista pienemmät muodot yhdistetyn kuvion sisällä. Tämä kuvio sisältää pyöreän alueen ja neliön. Jos löydät kummankin pinta-alan, voit löytää koko kuvion pinta-alan. |
|
|
|
Löydä neliön pinta-ala. |
|
|
|
|
Löydä ympyränmuotoisen alueen pintaala. Säde on 2 jalkaa. Huomaa, että alue on |
|
|
4 jalkaa2 + |
Lisää molemmat alueet yhteen. Koska mittaamasi ympyrän pinta-ala on likimääräinen, myös kuvion pinta-ala on likimääräinen. |
|
Vastaus |
Pinta-ala on noin 13.42 jalkaa2. |
|
Mikä on alla olevan kuvion pinta-ala (sadasosan tarkkuudella)? (Molemmat pyöristetyt alueet ovat puoliympyröitä.)
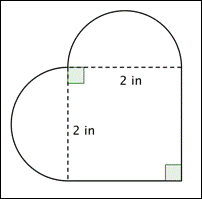
A) 16.56 in2
B) 7.14 in2
C) 4 in2
D) 3.14 in2
Yhteenveto
Ympyrä on tärkeä geometrinen muoto. Ympyrän ympärillä olevaa etäisyyttä kutsutaan kehäksi ja ympyrän sisätilaa pinta-alaksi. Ympyrän ympärysmitan ja pinta-alan laskemiseen tarvitaan luku nimeltä pi (![]() ), joka on päättymätön ja toistumaton desimaaliluku. Pi:tä approksimoidaan usein arvoilla 3,14 ja
), joka on päättymätön ja toistumaton desimaaliluku. Pi:tä approksimoidaan usein arvoilla 3,14 ja ![]() . Voit määrittää yhdistettyjen muotojen – myös ympyrän osia sisältävien muotojen – ympärysmitan tai pinta-alan soveltamalla tarvittaessa kehä- ja pinta-alakaavoja.
. Voit määrittää yhdistettyjen muotojen – myös ympyrän osia sisältävien muotojen – ympärysmitan tai pinta-alan soveltamalla tarvittaessa kehä- ja pinta-alakaavoja.