Objectifs d’apprentissage
- Connaître la relation entre la force de l’acide ou de la base et la magnitude de \(K_a\), \(K_b\), \(pK_a\), et \(pK_b\).
- Pour comprendre l’effet de nivellement.
La magnitude de la constante d’équilibre pour une réaction d’ionisation peut être utilisée pour déterminer les forces relatives des acides et des bases. Par exemple, l’équation générale pour l’ionisation d’un acide faible dans l’eau, où HA est l’acide parent et A- est sa base conjuguée, est la suivante :
\
La constante d’équilibre pour cette dissociation est la suivante :
\}{}. \label{16.5.2}\]
Comme nous l’avons noté précédemment, la concentration d’eau est essentiellement constante pour toutes les réactions en solution aqueuse, donc \(\) dans l’équation \(\ref{16.5.2}\) peut être incorporée dans une nouvelle quantité, la constante d’ionisation de l’acide (\(K_a\)), également appelée constante de dissociation de l’acide:
\=\dfrac{}{} \label{16.5.3}\]
Ainsi, les valeurs numériques de K et de \(K_a\) diffèrent par la concentration de l’eau (55,3 M). Encore une fois, pour simplifier, \(H_3O^+\) peut être écrit comme \(H^+\) dans l’équation \(\ref{16.5.3}\). Gardez cependant à l’esprit que le \(H^+\) libre n’existe pas dans les solutions aqueuses et qu’un proton est transféré au \(H_2O\) dans toutes les réactions d’ionisation acide pour former des ions hydronium, \(H_3O^+\). Plus le \(K_a\) est grand, plus l’acide est fort et plus la concentration en \(H^+\) est élevée à l’équilibre. Comme toutes les constantes d’équilibre, les constantes d’ionisation acide-base sont en fait mesurées en termes d’activités de \(H^+\) ou de \(OH^-\), ce qui les rend sans unité. Les valeurs de \(K_a\) pour un certain nombre d’acides courants sont données dans le tableau \(\PageIndex{1}\).
Les bases faibles réagissent avec l’eau pour produire l’ion hydroxyde, comme le montre l’équation générale suivante, où B est la base mère et BH+ est son acide conjugué:
\
La constante d’équilibre pour cette réaction est la constante d’ionisation de la base (Kb), également appelée constante de dissociation de la base:
\= \frac{}{}. \label{16.5.5}\]
Encore une fois, la concentration en eau est constante, elle n’apparaît donc pas dans l’expression de la constante d’équilibre ; en revanche, elle est incluse dans la \(K_b\). Plus le \(K_b\) est grand, plus la base est forte et plus la concentration en \(OH^-\) est élevée à l’équilibre. Les valeurs de \(K_b\) pour un certain nombre de bases faibles courantes sont données dans le tableau \(\PageIndex{2}\).
Il existe une relation simple entre la magnitude de \(K_a\) pour un acide et \(K_b\) pour sa base conjuguée. Considérons, par exemple, l’ionisation de l’acide cyanhydrique (\(HCN\)) dans l’eau pour produire une solution acide, et la réaction de \(CN^-\) avec l’eau pour produire une solution basique:
\
L’expression de la constante d’équilibre pour l’ionisation de HCN est la suivante:
\}{}. \label{16.5.8}\]
L’expression correspondante pour la réaction du cyanure avec l’eau est la suivante:
\}{} \label{16.5.9}\]
Si l’on ajoute les équations \(\ref{16.5.6}\) et \(\ref{16.5.7}\), nous obtenons ce qui suit:
| Réaction | Constantes d’équilibre |
|---|---|
| \(\cancel{HCN_{(aq)}}. \) | \(K_a=\cancel{}/\cancel{}\) |
| \(\cancel{CN^-_{(aq)}}+H_2O_{(l)} \rightleftharpoons OH^-_{(aq)}+\cancel{HCN_{(aq)}}\) | \(K_b=\cancel{}/\cancel{}\) |
| \(H_2O_{(l)} \N- H^+_{(aq)}+OH^-_{(aq)}\) | \N(K=K_a \times K_b=\) |
Dans ce cas, la somme des réactions décrites par \(K_a\) et \(K_b\) est l’équation de l’auto-ionisation de l’eau, et le produit des deux constantes d’équilibre est \(K_w\) :
\
Donc, si nous connaissons soit \(K_a\) pour un acide, soit \(K_b\) pour sa base conjuguée, nous pouvons calculer l’autre constante d’équilibre pour toute paire acide-base conjuguée.
Comme pour \(pH\), \(pOH\), et pKw, nous pouvons utiliser les logarithmes négatifs pour éviter la notation exponentielle dans l’écriture des constantes d’ionisation des acides et des bases, en définissant \(pK_a\) comme suit :
\
\
et \(pK_b\) comme
\
\
Similairement, l’équation \(\ref{16.5.10}\), qui exprime la relation entre \(K_a\) et \(K_b\), peut être écrite sous forme logarithmique comme suit :
\
À 25 °C, cela devient
\
Les valeurs de \(pK_a\) et \(pK_b\) sont données pour plusieurs acides et bases courants dans les tableaux \(\PageIndex{1}\) et \(\PageIndex{2}\), respectivement, et un ensemble plus complet de données est fourni dans les tableaux E1 et E2. En raison de l’utilisation de logarithmes négatifs, les plus petites valeurs de \(pK_a\) correspondent à des constantes d’ionisation d’acide plus grandes et donc à des acides plus forts. Par exemple, l’acide nitreux (\(HNO_2\)), avec une \(pK_a\) de 3,25, est un acide environ un million de fois plus fort que l’acide cyanhydrique (HCN), avec une \(pK_a\) de 9,21. À l’inverse, les plus petites valeurs de \(pK_b\) correspondent à des constantes d’ionisation de base plus grandes et donc à des bases plus fortes.
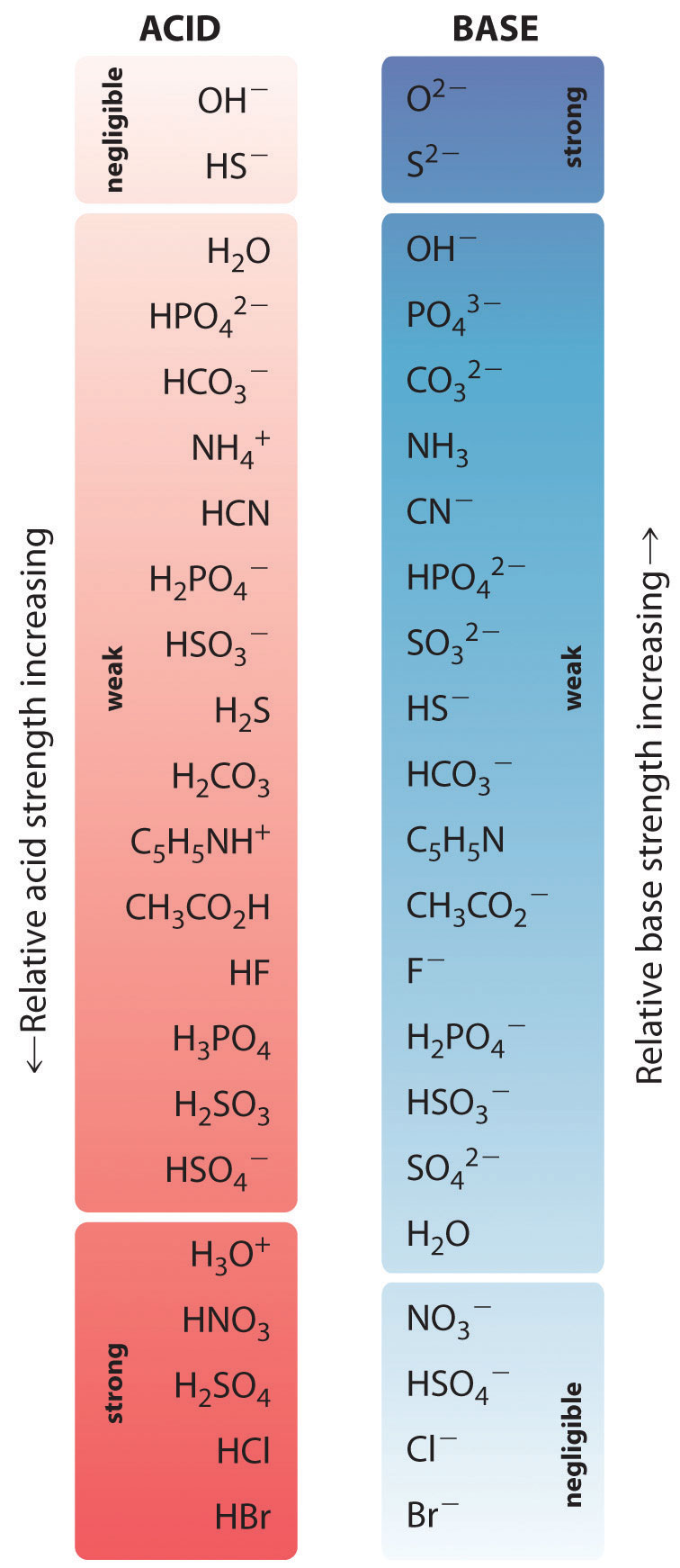
Les forces relatives de certains acides courants et de leurs bases conjuguées sont représentées graphiquement dans la figure \(\PageIndex{1}\). Les paires acide-base conjuguées sont classées par ordre (de haut en bas) de force croissante de l’acide, ce qui correspond à des valeurs décroissantes de \(pK_a\). Cet ordre correspond à une force décroissante de la base conjuguée ou à des valeurs croissantes de \(pK_b\). En bas à gauche de la figure \(\PageIndex{2}\) se trouvent les acides forts les plus courants ; en haut à droite se trouvent les bases fortes les plus courantes. Remarquez la relation inverse entre la force de l’acide parent et la force de la base conjuguée. Ainsi, la base conjuguée d’un acide fort est une base très faible, et la base conjuguée d’un acide très faible est une base forte.
La base conjuguée d’un acide fort est une base faible et vice versa.
Nous pouvons utiliser les forces relatives des acides et des bases pour prédire la direction d’une réaction acide-base en suivant une seule règle : un équilibre acide-base favorise toujours le côté avec l’acide et la base les plus faibles, comme indiqué par ces flèches :
\
Dans une réaction acide-base, le proton réagit toujours avec la base la plus forte.
Par exemple, l’acide chlorhydrique est un acide fort qui s’ionise essentiellement complètement en solution aqueuse diluée pour produire du \(H_3O^+\) et du \(Cl^-\) ; seules des quantités négligeables de molécules de \(HCl\) restent non dissociées. Par conséquent, l’équilibre d’ionisation se trouve pratiquement tout à fait à droite, comme représenté par une seule flèche :
\
En revanche, l’acide acétique est un acide faible, et l’eau est une base faible. Par conséquent, les solutions aqueuses d’acide acétique contiennent principalement des molécules d’acide acétique en équilibre avec une petite concentration de \(H_3O^+\) et d’ions acétate, et l’équilibre d’ionisation se situe loin vers la gauche, comme représenté par ces flèches:
De même, dans la réaction de l’ammoniac avec l’eau, l’ion hydroxyde est une base forte, et l’ammoniac est une base faible, alors que l’ion ammonium est un acide plus fort que l’eau. Par conséquent, cet équilibre se situe également à gauche:
\
Tous les équilibres acide-base favorisent le côté avec l’acide et la base les plus faibles. Ainsi le proton est lié à la base la plus forte.
Exemple \(\PageIndex{1}\) : Ions butyrate et diméthylammonium
- Calculez le \(K_b\) et le \(pK_b\) de l’ion butyrate (\(CH_3CH_2CH_2CO_2^-\)). Le \(pK_a\) de l’acide butyrique à 25°C est de 4,83. L’acide butyrique est responsable de l’odeur nauséabonde du beurre rance.
- Calculez le \(K_a\) et le \(pK_a\) de l’ion diméthylammonium (\((CH_3)_2NH_2^+\)). La constante d’ionisation de base \(K_b\) de la diméthylamine (\((CH_3)_2NH\)) est \(5,4 \times 10^{-4}\) à 25°C.
Donné : \(pK_a\) et \(K_b\)
Demande : \(K_b\) et \(pK_b\) correspondants, \(K_a\) et \(pK_a\)
Stratégie :
Les constantes \(K_a\) et \(K_b\) sont liées comme indiqué dans l’équation \(\ref{16.5.10}\). Les constantes \(pK_a\) et \(pK_b\) d’un acide et de sa base conjuguée sont liées comme le montrent les équations \(\ref{16.5.15}\) et \(\ref{16.5.16}\). Utilisez les relations pK = -log K et K = 10-pK (équations \(\ref{16.5.11}\) et \(\ref{16.5.13}\)) pour convertir entre \(K_a\) et \(pK_a\) ou \(K_b\) et \(pK_b\).
Solution:
On nous donne le \(pK_a\) de l’acide butyrique et on nous demande de calculer le \(K_b\) et le \(pK_b\) de sa base conjuguée, l’ion butyrate. Comme la valeur du \(pK_a\) citée correspond à une température de 25°C, nous pouvons utiliser l’équation \(\ref{16.5.16}\) : \(pK_a\) + \(pK_b\) = pKw = 14,00. En substituant le \(pK_a\) et en résolvant le \(pK_b\),
Parce que \(pK_b = -\log K_b\), \(K_b\) est \(10^{-9.17} = 6.8 \times 10^{-10}\).
Dans ce cas, on nous donne \(K_b\) pour une base (diméthylamine) et on nous demande de calculer \(K_a\) et \(pK_a\) pour son acide conjugué, l’ion diméthylammonium. Comme la quantité initiale donnée est \(K_b\) plutôt que \(pK_b\), nous pouvons utiliser l’équation \(\ref{16.5.10}\) : \(K_aK_b = K_w\). En substituant les valeurs de \(K_b\) et \(K_w\) à 25°C et en résolvant pour \(K_a\),
\
\
Parce que \(pK_a\) = -log \(K_a\), nous avons \(pK_a = -\log(1,9 \times 10^{-11}) = 10,72\). Nous aurions également pu convertir \(K_b\) en \(pK_b\) pour obtenir la même réponse :
Si on nous donne l’une de ces quatre quantités pour un acide ou une base (\(K_a\), \(pK_a\), \(K_b\), ou \(pK_b\)), nous pouvons calculer les trois autres.
Exercice \(\NPageIndex{1}\) : Acide lactique
L’acide lactique (\(CH_3CH(OH)CO_2H\)) est responsable du goût et de l’odeur piquants du lait aigre ; on pense également qu’il produit des douleurs dans les muscles fatigués. Son \(pK_a\) est de 3,86 à 25°C. Calculez le \(K_a\) de l’acide lactique et les \(pK_b\) et \(K_b\) de l’ion lactate.
Réponse
- \(K_a = 1,4 \times 10^{-4}\) pour l’acide lactique;
- \(pK_b\) = 10.14 et
- \(K_b = 7,2 \times 10^{-11}\) pour l’ion lactate
Solutions d’acides et de bases forts : The Leveling Effect
Vous remarquerez dans le tableau \(\PageIndex{1}\) que les acides comme \(H_2SO_4\) et \(HNO_3\) se trouvent au-dessus de l’ion hydronium, ce qui signifie qu’ils ont des valeurs \(pK_a\) inférieures à zéro et sont des acides plus forts que l’ion \(H_3O^+\). Rappelez-vous du chapitre 4 que le proton acide de pratiquement tous les oxoacides est lié à l’un des atomes d’oxygène de l’oxoanion. Ainsi, l’acide nitrique devrait s’écrire correctement : \(HONO_2\). Malheureusement, les formules des oxoacides sont presque toujours écrites avec l’hydrogène à gauche et l’oxygène à droite, ce qui donne \(HNO_3\). En fait, les six acides forts courants que nous avons rencontrés pour la première fois au chapitre 4 ont tous une valeur de \(pK_a\) inférieure à zéro, ce qui signifie qu’ils ont une plus grande tendance à perdre un proton que l’ion \(H_3O^+\). À l’inverse, les bases conjuguées de ces acides forts sont des bases plus faibles que l’eau. Par conséquent, les équilibres de transfert de protons de ces acides forts se situent loin vers la droite, et l’ajout de n’importe lequel des acides forts courants à l’eau entraîne une réaction essentiellement stœchiométrique de l’acide avec l’eau pour former une solution de l’ion \(H_3O^+\) et de la base conjuguée de l’acide.
Bien que \(K_a\) pour \(HI\) soit environ 108 plus grand que \(K_a\) pour \(HNO_3\), la réaction de \(HI\) ou de \(HNO_3\) avec l’eau donne une solution essentiellement stœchiométrique de \(H_3O^+\) et I- ou \(NO_3^-\). En fait, une solution aqueuse 0,1 M de tout acide fort contient en réalité 0,1 M de \(H_3O^+\), quelle que soit l’identité de l’acide fort. Ce phénomène est appelé effet de nivellement : toute espèce qui est un acide plus fort que l’acide conjugué de l’eau (\(H_3O^+\)) est nivelée à la force de \(H_3O^+\) en solution aqueuse parce que \(H_3O^+\) est l’acide le plus fort qui peut exister en équilibre avec l’eau. Par conséquent, il est impossible de distinguer les forces des acides tels que HI et HNO3 en solution aqueuse, et une approche alternative doit être utilisée pour déterminer leurs forces acides relatives.
Une méthode consiste à utiliser un solvant tel que l’acide acétique anhydre. Puisque l’acide acétique est un acide plus fort que l’eau, il doit également être une base plus faible, avec une moindre tendance à accepter un proton que \(H_2O\). Les mesures de la conductivité de solutions 0,1 M de HI et de \(HNO_3\) dans l’acide acétique montrent que HI est complètement dissocié, mais que \(HNO_3\) n’est que partiellement dissocié et se comporte comme un acide faible dans ce solvant. Ce résultat nous indique clairement que HI est un acide plus fort que \(HNO_3\). L’ordre relatif des forces des acides et les valeurs approximatives de \(K_a\) et \(pK_a\) pour les acides forts en haut du tableau \(\PageIndex{1}\) ont été déterminés en utilisant des mesures comme celle-ci et différents solvants non aqueux.
Dans les solutions aqueuses, \(H_3O^+\) est l’acide le plus fort et \(OH^-\) est la base la plus forte qui peut exister en équilibre avec \(H_2O\).
L’effet de nivellement s’applique également aux solutions de bases fortes : En solution aqueuse, toute base plus forte que OH- est nivelée à la force de OH- car OH- est la base la plus forte qui peut exister en équilibre avec l’eau. Les sels tels que \(K_2O\), \(NaOCH_3\) (méthoxyde de sodium), et \(NaNH_2\) (sodamide, ou amide de sodium), dont les anions sont les bases conjuguées des espèces qui se situeraient en dessous de l’eau dans le tableau \(\PageIndex{2}\), sont tous des bases fortes qui réagissent essentiellement complètement (et souvent violemment) avec l’eau, acceptant un proton pour donner une solution de \(OH^-\) et le cation correspondant :
\
\
\
D’autres exemples que vous pouvez rencontrer sont l’hydrure de potassium (\(KH\)) et les composés organométalliques tels que le méthyl-lithium (\(CH_3Li\)).
Acides et bases polyprotiques
Comme vous l’avez appris, les acides polyprotiques tels que \(H_2SO_4\), \(H_3PO_4\), et \(H_2CO_3\) contiennent plus d’un proton ionisable, et les protons sont perdus de manière progressive. L’espèce entièrement protonée est toujours l’acide le plus fort, car il est plus facile d’enlever un proton à une molécule neutre qu’à un ion chargé négativement. Ainsi, la force de l’acide diminue avec la perte des protons suivants et, en conséquence, le \(pK_a\) augmente. Considérons par exemple \(H_2SO_4\):
\
L’équilibre dans la première réaction se trouve loin vers la droite, ce qui est cohérent avec le fait que \(H_2SO_4\) est un acide fort. En revanche, dans la deuxième réaction, des quantités appréciables de \(HSO_4^-\) et de \(SO_4^{2-}\) sont présentes à l’équilibre.
Pour un acide polyprotique, la force de l’acide diminue et le \(pK_a\) augmente avec la perte séquentielle de chaque proton.
L’ion sulfate d’hydrogène (\(HSO_4^-\)) est à la fois la base conjuguée de \(H_2SO_4\) et l’acide conjugué de \(SO_4^{2-}\). Tout comme l’eau, HSO4- peut donc agir comme un acide ou une base, selon que l’autre réactif est un acide plus fort ou une base plus forte. À l’inverse, l’ion sulfate (\(SO_4^{2-}\)) est une base polyprotique capable d’accepter deux protons de manière progressive:
\
\
Comme toute autre paire acide-base conjuguée, les forces des acides et des bases conjugués sont liées par \(pK_a\) + \(pK_b\) = pKw. Considérons, par exemple, le couple acide-base conjugué \(HSO_4^-/ SO_4^{2-}\). D’après le tableau \(\PageIndex{1}\), nous voyons que le \(pK_a\) de \(HSO_4^-\) est de 1,99. Par conséquent, le \(pK_b\) du\(SO_4^{2-}\) est de 14,00 – 1,99 = 12,01. Ainsi, le sulfate est une base plutôt faible, alors que le \(OH^-\) est une base forte, donc l’équilibre montré dans l’équation \(\ref{16.6}\) se trouve à gauche. L’ion \(HSO_4^-\) est également une base très faible (\(pK_a\) de \(H_2SO_4\) = 2,0, \(pK_b\) de \(HSO_4^- = 14 – (-2,0) = 16\)), ce qui est conforme à ce que nous attendons pour la base conjuguée d’un acide fort.
Exemple \(\PageIndex{2}\)
Prédisez si l’équilibre de chaque réaction se situe à gauche ou à droite comme écrit.
- \(NH^+_{4(aq)}+PO^{3-}_{4(aq)} \rightleftharpoons NH_{3(aq)}+HPO^{2−}_{4(aq)}\)
- \(CH_3CH_2CO_2H_{(aq)}+CN^−_{(aq)} \rightleftharpoons CH_3CH_2CO^-_{2(aq)}+HCN_{(aq)}\)
Donné : équation chimique équilibrée
Demandé : position d’équilibre
Stratégie:
Identifiez les paires acide-base conjuguées dans chaque réaction. Consultez ensuite les tableaux \(\PageIndex{1}\)et \(\PageIndex{2}\) et la figure \(\PageIndex{2}\) pour déterminer quel est l’acide et la base les plus forts. L’équilibre favorise toujours la formation du couple acide-base le plus faible.
Solution:
Les couples acide-base conjugués sont \(NH_4^+/NH_3\) et \(HPO_4^{2-}/PO_4^{3-}\). Selon les tableaux \(\PageIndex{1}\) et \(\PageIndex{2}\), \(NH_4^+\) est un acide plus fort (\(pK_a = 9.25\)) que \(HPO_4^{2-}\) (pKa = 12,32), et \(PO_4^{3-}\) est une base plus forte (\(pK_b = 1,68\)) que \(NH_3\) (\(pK_b = 4,75\)). L’équilibre se situe donc vers la droite, favorisant la formation du couple acide-base le plus faible :
\
Les couples acide-base conjugués sont \(CH_3CH_2CO_2H/CH_3CH_2CO_2^-\) et \(HCN/CN^-\). Selon le tableau \(\PageIndex{1}\), HCN est un acide faible (pKa = 9,21) et \(CN^-\) est une base modérément faible (pKb = 4,79). Cependant, l’acide propionique (\(CH_3CH_2CO_2H\)) ne figure pas dans le tableau \(\PageIndex{1}\). Dans une telle situation, la meilleure approche consiste à rechercher un composé similaire dont les propriétés acide-base sont répertoriées. Par exemple, l’acide propionique et l’acide acétique sont identiques à l’exception des groupes attachés à l’atome de carbone de l’acide carboxylique (\(\ce{-CH_2CH_3}\) versus \(\ce{-CH_3}\)), on peut donc s’attendre à ce que les deux composés aient des propriétés acido-basiques similaires. En particulier, on peut s’attendre à ce que la valeur du \(pK_a\) de l’acide propionique soit similaire à celle du \(pK_a\) de l’acide acétique. (En fait, le \(pK_a\) de l’acide propionique est de 4,87, contre 4,76 pour l’acide acétique, ce qui fait de l’acide propionique un acide légèrement plus faible que l’acide acétique). Ainsi, l’acide propionique devrait être un acide nettement plus fort que l’acide \(HCN\). Comme l’acide le plus fort forme la base conjuguée la plus faible, nous prédisons que le cyanure sera une base plus forte que le propionate. L’équilibre se situera donc à droite, favorisant la formation du couple acide-base le plus faible :
\
Exercice \(\PageIndex{1}\)
Prédisez si l’équilibre de chaque réaction se situe à gauche ou à droite comme écrit.
- \(H_2O_{(l)}+HS^-_{(aq)} \rightleftharpoons OH^−_{(aq)}+H_2S_{(aq)}\)
- \(HCO^−_{2(aq)}+HSO^−_{4(aq)} \{rightleftharpoons HCO_2H_{(aq)}+SO^{2-}_{4(aq)}\)
Réponse a
gauche
Réponse b
gauche
Sommaire
Les réactions acide-base contiennent toujours deux paires acide-base conjuguées. A chaque acide et à chaque base est associée une constante d’ionisation qui correspond à sa force acide ou basique. Deux espèces qui ne diffèrent que par un proton constituent une paire acide-base conjuguée. L’amplitude de la constante d’équilibre pour une réaction d’ionisation peut être utilisée pour déterminer les forces relatives des acides et des bases. Pour une solution aqueuse d’un acide faible, la constante de dissociation est appelée constante d’ionisation de l’acide (\(K_a\)). De même, la constante d’équilibre pour la réaction d’une base faible avec l’eau est la constante d’ionisation de la base (\(K_b\)). Pour tout couple acide-base conjugué, \(K_aK_b = K_w\). Des valeurs plus petites de \(pK_a\) correspondent à des constantes d’ionisation d’acide plus grandes et donc à des acides plus forts. Inversement, de plus petites valeurs de \(pK_b\) correspondent à de plus grandes constantes d’ionisation des bases et donc à des bases plus fortes. À 25°C, \(pK_a + pK_b = 14,00\). Les réactions acide-base se déroulent toujours dans le sens qui produit le couple acide-base le plus faible. Aucun acide plus fort que \(H_3O^+\) et aucune base plus forte que \(OH^-\) ne peuvent exister en solution aqueuse, ce qui conduit au phénomène connu sous le nom d’effet de nivellement. Les acides (et les bases) polyprotiques perdent (et gagnent) des protons de manière progressive, l’espèce entièrement protonée étant l’acide le plus fort et l’espèce entièrement déprotonée la base la plus forte.
Équations clés
- Constante d’ionisation de l’acide : \=\dfrac{}{} \]
- Constante d’ionisation de base : \= \dfrac{}{} \]
- Relation entre \(K_a\) et \(K_b\) d’une paire acide-base conjuguée : \
- Définition de \(pK_a\) : \
- Définition de \(pK_b\) : \
- Relation entre \(pK_a\) et \(pK_b\) d’une paire acide-base conjuguée : \\N
Contributeurs et attributions
-
Stephen Lower, professeur émérite (Simon Fraser U.) Manuel virtuel de chimie
.