Objectifs pédagogiques
- Comprendre la représentation 3D des orbitales électroniques
Une orbitale est le raffinement mécanique quantique de l’orbite de Bohr. Contrairement à son concept d’une orbite circulante simple avec un rayon fixe, les orbitales sont des régions de l’espace dérivées mathématiquement avec différentes probabilités de contenir un électron.
Une façon de représenter les distributions de probabilité des électrons a été illustrée précédemment fo(r\) l’orbitale 1s de l’hydrogène. Comme Ψ2 donne la probabilité de trouver un électron dans un volume d’espace donné (tel qu’un picomètre cube), un tracé de Ψ2 en fonction de la distance au noyau (r) est un tracé de la densité de probabilité. L’orbitale 1s étant à symétrie sphérique, la probabilité de trouver un électron 1s en un point donné ne dépend que de sa distance au noyau. La densité de probabilité est maximale à \(\(r\) = 0\) (au niveau du noyau) et diminue régulièrement avec l’augmentation de la distance. Pour de très grandes valeurs de r, la densité de probabilité de l’électron est très faible mais pas nulle.
En revanche, nous pouvons calculer la probabilité radiale (la probabilité de trouver un électron 1s à une distance \(r\) du noyau) en additionnant ensemble\(r\) les probabilités qu’un électron soit en tous points d’une série de x coquilles sphériques de rayon r1, r2, r3,…, rx – 1, rx. En fait, nous divisons l’atome en coquilles concentriques très fines, un peu comme les couches d’un oignon (Figure \(\PageIndex{1a}\)), et nous calculons la probabilité de trouver un électron sur chaque coquille sphérique. Rappelez-vous que la densité de probabilité des électrons est maximale à \(r\) = 0 (Figure \(\PageIndex{1b}\)), la densité des points est donc maximale pour \(r\) les plus petites coquilles sphériques de la partie (a) de la Figure \(\PageIndex{1}\). En revanche, la surface de chaque coque sphérique est égale à \(4πr^2\), qui augmente très rapidement avec l’augmentation de \(r\) (figure \(\PageIndex{1c}\)). Étant donné que la surface des enveloppes sphériques augmente plus rapidement avec l’augmentation de \(r\) que la densité de probabilité des électrons ne diminue, le tracé de la probabilité radiale présente un maximum à une distance particulaire \(r\) (figure \(\PageIndex{1d}\)). Plus important encore, lorsque \(r\) est très petit, la surface d’une coquille sphérique est si petite que la probabilité totale de trouver un électron près du noyau est très faible ; au niveau du noyau, la probabilité de l’électron disparaît (Figure \(\PageIndex{1d}\)).

Pour l’atome d’hydrogène, le pic dans le tracé de probabilité radiale se produit à \(r\) = 0,529 Å (52,9 pm), qui est exactement le rayon calculé par Boh\(r\) pour l’orbite n = 1. Ainsi, le rayon le plus probable obtenu par la mécanique quantique est identique au rayon calculé par la mécanique classique. Cependant, dans le modèle de Bohr, l’électron était supposé se trouver à cette distance 100 % du temps, alors que dans le modèle de Schrödinge(r\), il ne se trouve à cette distance qu’une partie du temps. La différence entre les deux modèles est attribuable au comportement ondulatoire de l’électron et au principe d’incertitude d’Heisenberg.
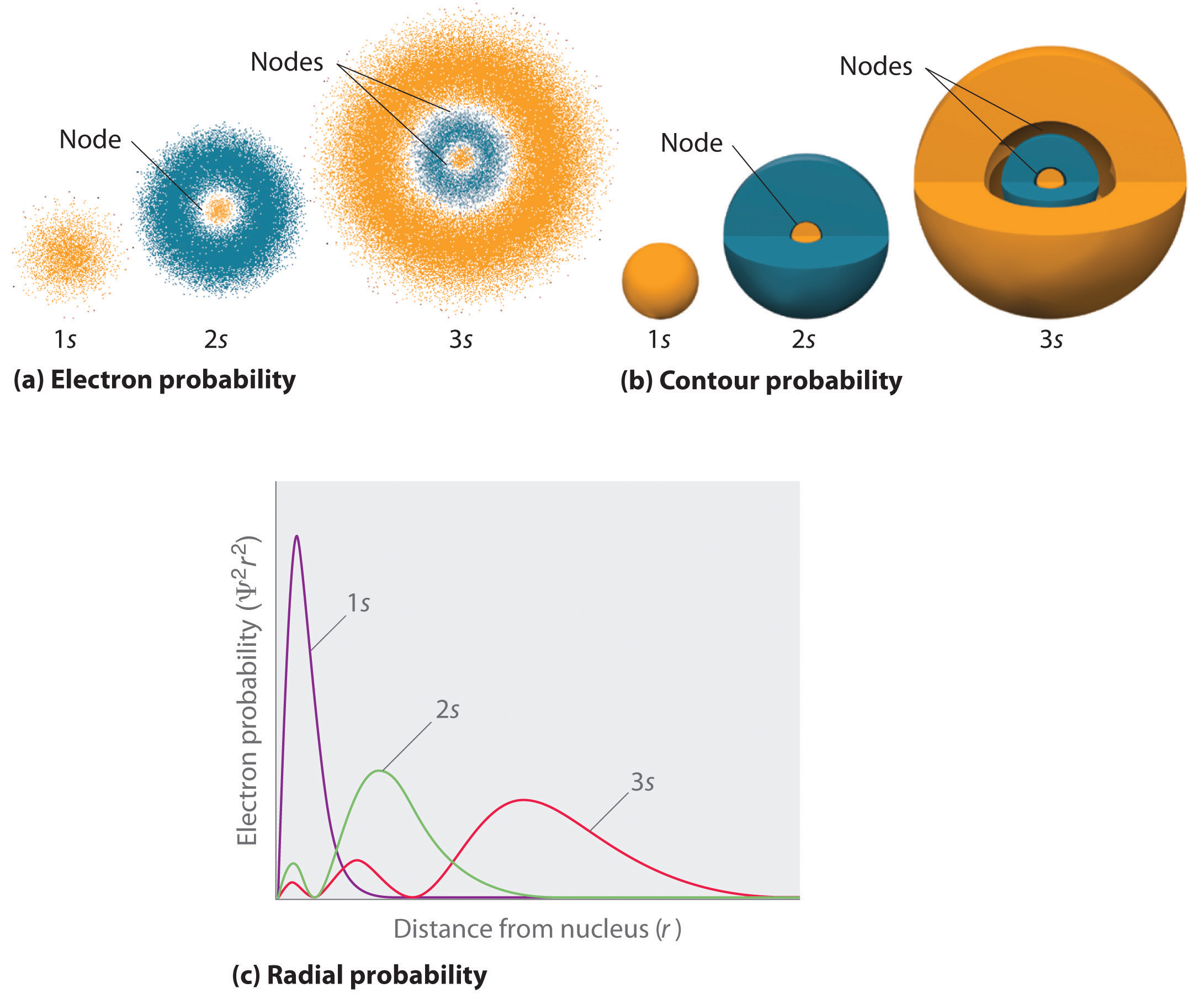
La figure \(\PageIndex{2}\) compare les densités de probabilité des électrons pour les orbitales 1s, 2s et 3s de l’hydrogène. Notez que toutes les trois sont sphériquement symétriques. Pour les orbitales 2s et 3s, cependant (et pour toutes les autres orbitales s également), la densité de probabilité des électrons ne diminue pas de manière régulière lorsque \(r\) augmente. Au contraire, une série de minima et de maxima est observée dans les tracés de probabilité radiale (figure \(\PageIndex{2c}\)). Les minima correspondent à des nœuds sphériques (régions de probabilité électronique nulle), qui alternent avec des régions sphériques de probabilité électronique non nulle. L’existence de ces nœuds est une conséquence des changements de phase d’onde dans la fonction d’onde Ψ.
Orbitales s (l=0)
Trois choses arrivent aux orbitales s lorsque n augmente (figure \(\PageIndex{2}\)):
- Elles deviennent plus grandes, s’étendant plus loin du\\\Noyau.
- Elles contiennent plus de nœuds. Ceci est similaire à une onde stationnaire qui a des régions d’amplitude significative séparées par des nœuds, des points d’amplitude nulle.
- Pour un atome donné, les orbitales s deviennent également plus élevées en énergie lorsque n augmente en raison de la distance accrue du noyau.
Les orbitales sont généralement dessinées comme des surfaces tridimensionnelles qui englobent 90 % de la densité électronique, comme cela a été montré pour les orbitales 1s, 2s et 3s de l’hydrogène dans la partie (b) de la figure \(\PageIndex{2}\). Bien que de tels dessins montrent les tailles relatives des orbitales, ils ne montrent normalement pas les nœuds sphériques des orbitales 2s et 3s, car les nœuds sphériques se trouvent à l’intérieur de la surface de 90 %. Heureusement, les positions des nœuds sphériques ne sont pas importantes pour la liaison chimique.
Orbitales p (l=1)
Seules les orbitales s sont sphériquement symétriques. Plus la valeur de l augmente, plus le nombre d’orbitales dans une sous-coquille donnée augmente, et plus les formes des orbitales deviennent complexes. Comme la sous-coquille 2p a l = 1, avec trois valeurs de ml (-1, 0 et +1), il y a trois orbitales 2p.
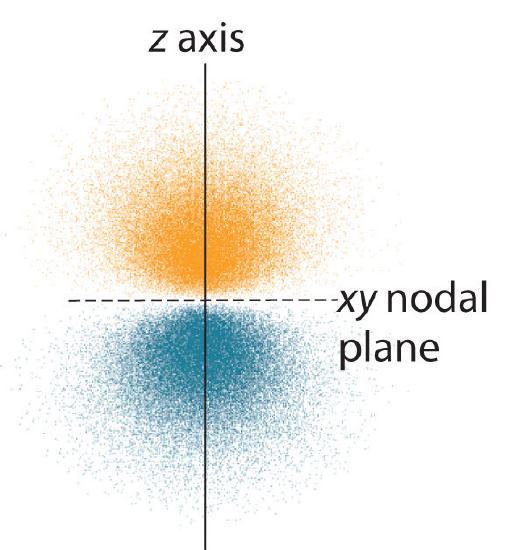
La distribution de probabilité des électrons fo\(r\) l’une des orbitales 2p de l’hydrogène est illustrée sur la figure \(\PageIndex{3}\). Comme cette orbitale présente deux lobes de densité électronique disposés le long de l’axe z, avec une densité électronique nulle dans le plan xy (c’est-à-dire que le plan xy est un plan nodal), il s’agit d’une orbitale \(2p_z\). Comme le montre la figure \(\PageIndex{4}\), les deux autres orbitales 2p ont des formes identiques, mais elles se trouvent respectivement le long de l’axe x (\(2p_x\)) et de l’axe y (\(2p_y\)). Notez que chaque orbitale p n’a qu’un seul plan nodal. Dans chaque cas, la phase de la fonction d’onde fo\(r\) de chacune des orbitales 2p est positive fo\(r\) le lobe qui pointe le long de l’axe positif et négative fo\(r\) le lobe qui pointe le long de l’axe négatif. Il est important de souligner que ces signes correspondent à la phase de l’onde qui décrit le mouvement de l’électron, et non à des charges positives o\(r\) négatives.
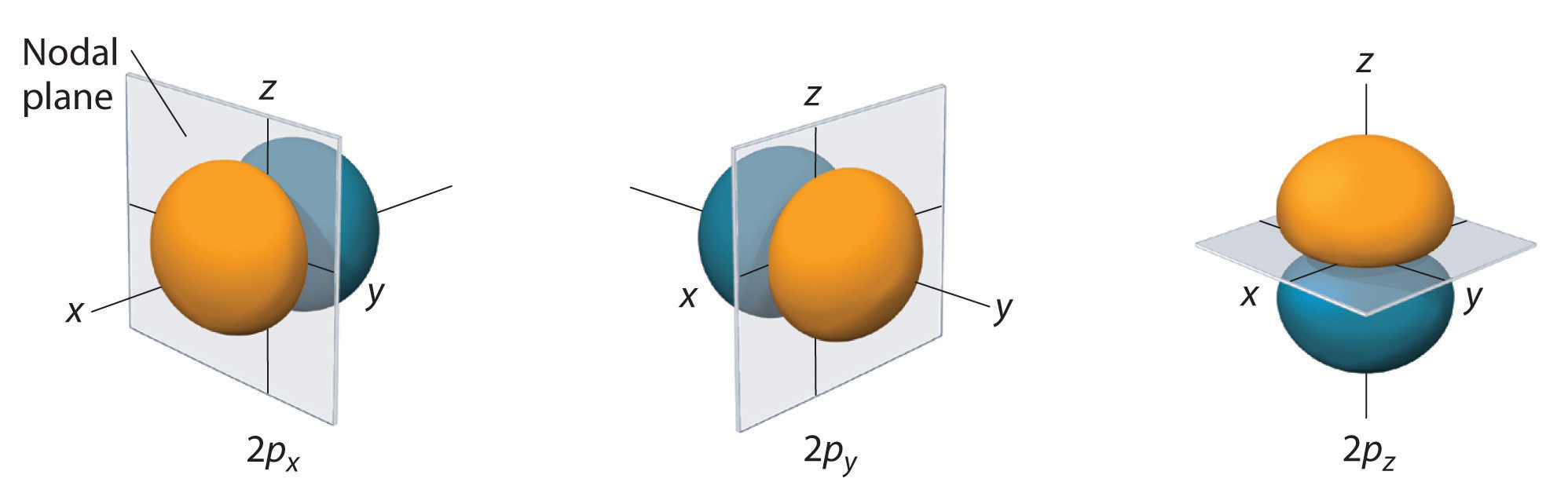
Les surfaces représentées enferment 90% de la probabilité totale de l’électron fo\(r\) les orbitales 2px, 2py, et 2pz. Chaque orbitale est orientée selon l’axe indiqué par l’indice et un plan nodal perpendiculaire à cet axe coupe chaque orbitale 2p. La phase de la fonction d’onde est positive (orange) dans la région de l’espace où x, y, o\(r\) z est positif et négative (bleu) où x, y, o\(r\) z est négatif. Tout comme pour les orbitales s, la taille et la complexité des orbitales p d’un atome augmentent à mesure que le nombre quantique principal n augmente. Les formes des surfaces de probabilité à 90 % des orbitales p 3p, 4p et de plus haute énergie sont toutefois essentiellement les mêmes que celles illustrées sur la figure \(\PageIndex{4}\).
Orbitales d (l=2)
Les sous-coquilles avec l = 2 ont cinq orbitales d ; la première coquille principale à avoir une sous-coquille d correspond à n = 3. Les cinq orbitales d ont des valeurs ml de -2, -1, 0, +1, et +2.
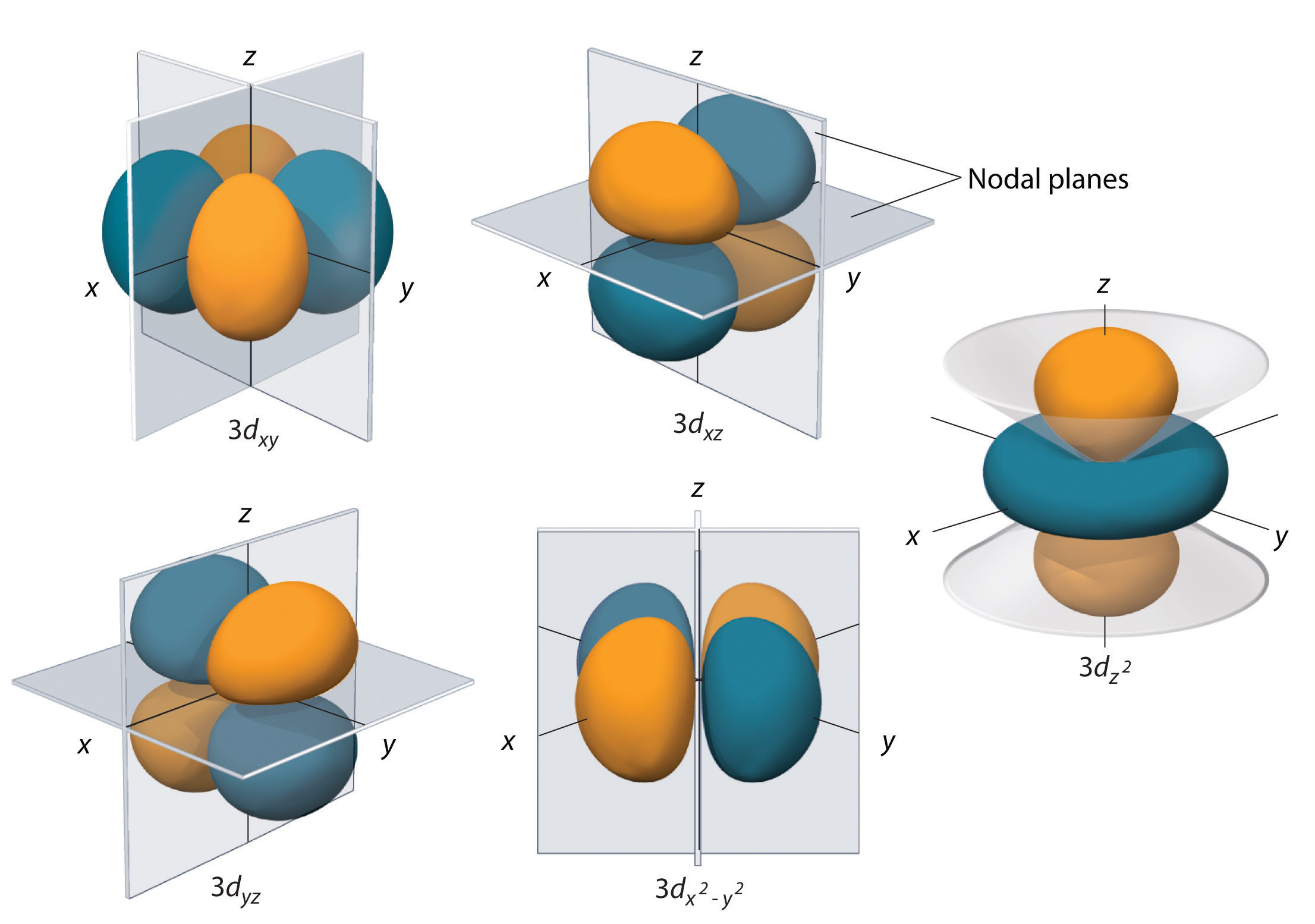
Les orbitales 3d de l’hydrogène, représentées sur la figure \(\PageIndex{5}\), ont des formes plus complexes que les orbitales 2p. Les cinq orbitales 3d contiennent toutes deux des surfaces nodales, contre une pour chaque orbitale p et zéro pour chaque orbitale s. Dans trois des orbitales d, les lobes de densité électronique sont orientés entre les plans x et y, x et z, et y et z ; ces orbitales sont appelées respectivement orbitales \(3d_{xy}\), \(3d_{xz}\) et \(3d_{yz}\). Une quatrième orbitale d possède des lobes situés le long des axes x et y ; il s’agit de l’orbitale \(3d_{x^2-y^2}\). La cinquième orbitale 3d, appelée orbitale \(3d_{z^2}\), a une forme unique : elle ressemble à une orbitale \(2p_z\) combinée à un beignet supplémentaire de probabilité électronique situé dans le plan xy. Malgré sa forme particulière, l’orbitale \(3d_{z^2}\) est mathématiquement équivalente aux autres orbitales \(r\) et possède la même énergie. Contrairement aux orbitales p, la phase de la fonction d’onde des orbitales d est la même pour les paires de lobes opposés. Comme le montre la figure, la phase de la fonction d’onde est positive pour les deux lobes de l’orbitale dz^2 qui se trouvent le long de l’axe z, tandis que la phase de la fonction d’onde est négative pour le beignet de densité électronique dans le plan xy. Comme pour les orbitales s et p, lorsque n augmente, la taille des orbitales d augmente, mais les formes générales restent similaires à celles représentées sur la figure \(\PageIndex{5}\).
Orbitales f (l=3)
Les coquilles principales avec n = 4 peuvent avoir des sous-coquilles avec l = 3 et des valeurs ml de -3, -2, -1, 0, +1, +2 et +3. Ces sous-coquilles sont composées de sept orbitales f. Chaque orbitale f possède trois surfaces nodales, de sorte que les formes i(r\) sont complexes. Comme les orbitales f ne sont pas particulièrement importantes pour nous, nous n’en parlons pas davantage, et les orbitales avec des valeurs élevées de l ne sont pas discutées du tout.
Énergies orbitales
Bien que nous ayons discuté des formes des orbitales, nous avons peu parlé de leurs énergies comparatives. Nous commençons notre discussion sur les énergies orbitales en considérant les atomes ou les ions avec un seul électron (comme H o\(r\) He+).
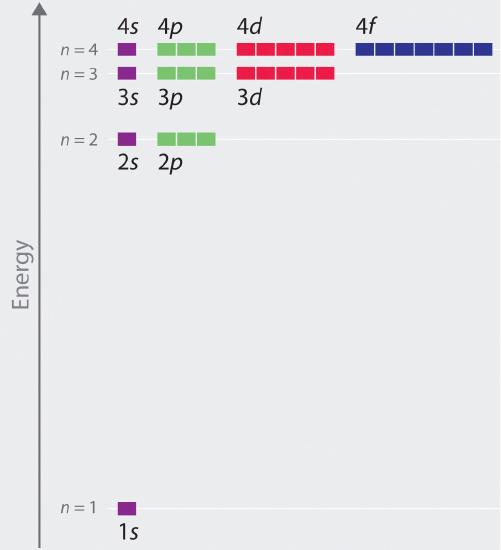
Les énergies relatives des orbitales atomiques avec n ≤ 4 pour un atome d’hydrogène sont représentées sur la figure \(\PageIndex{6}\) ; notez que les énergies orbitales dépendent uniquement du nombre quantique principal n. Par conséquent, les énergies des orbitales 2s et 2p de l’hydrogène sont les mêmes ; les énergies des orbitales 3s, 3p et 3d sont les mêmes, et ainsi de suite. La mécanique quantique prévoit que dans l’atome d’hydrogène, toutes les orbitales ayant la même valeur de n (par exemple, les trois orbitales 2p) sont dégénérées, ce qui signifie qu’elles ont la même énergie. Les énergies des orbitales obtenues pour l’hydrogène en utilisant la mécanique quantique sont exactement les mêmes que les énergies autorisées calculées par Bohème. Cependant, contrairement au modèle de Bohr, qui n’autorisait qu’une seule orbitale par niveau d’énergie, la mécanique quantique prédit qu’il existe 4 orbitales avec des distributions de densité électronique différentes dans la couche principale n = 2 (une orbitale 2s et trois orbitales 2p), 9 dans la couche principale n = 3 et 16 dans la couche principale n = 4.Les différentes valeurs de l et ml des orbitales individuelles dans une coquille principale donnée ne sont pas importantes pour comprendre les spectres d’émission ou d’absorption de l’atome d’hydrogène dans la plupart des conditions, mais elles expliquent les dédoublements des raies principales observés lorsque les atomes d’hydrogène sont placés dans un champ magnétique. La figure \(\PageIndex{6}\) montre que les niveaux d’énergie deviennent proches\(r\) et proches\(r\) l’un de l’autre quand la valeur de n augmente, comme prévu en raison de la dépendance 1/n2 des énergies orbitales.
Les énergies des orbitales dans toute espèce avec un seul électron peuvent être calculées par une variation mino\(r\) de l’équation de Bohr, qui peut être étendue à d’autres espèces à un seul électron en incorporant la charge du noyau\(r\) \(Z\) (le nombre\(r\) de protons dans le noyau) :
\
En général, l’énergie et le rayon diminuent lorsque la charge du noyau augmente. Ainsi, les orbitales les plus stables (celles dont l’énergie est la plus faible) sont celles qui sont les plus proches du noyau. Par exemple, dans l’état fondamental de l’atome d’hydrogène, l’électron unique se trouve sur l’orbitale 1s, alors que dans le premier état excité, l’atome a absorbé de l’énergie et l’électron a été promu sur l’une des orbitales n = 2. Dans les ions avec un seul électron, l’énergie d’une orbitale donnée ne dépend que de n, et toutes les sous-coquilles au sein d’une coquille principale, telles que les orbitales \(p_x\), \(p_y\) et \(p_z\), sont dégénérées.
Résumé
Les principaux types d’orbitales atomiques chimiquement importants correspondent aux valeurs de \(\ell = 0\), \(1\), \(2\), et \(3\). Les orbitales avec \(\ell = 0\) sont des orbitales s et sont sphériquement symétriques, la plus grande probabilité de trouver l’électron se trouvant au niveau du noyau. Toutes les orbitales dont les valeurs sont \(n > 1\) et \(ell = 0\) contiennent un ou plusieurs nœuds. Les orbitales avec \(\ell = 1\) sont des orbitales p et contiennent un plan nodal qui inclut le noyau, ce qui donne lieu à une forme d’haltère. Les orbitales avec \(\ell = 2\) sont des orbitales d et ont des formes plus complexes avec au moins deux surfaces nodales. Les orbitales avec \(\ell = 3\) sont des orbitales f, qui sont encore plus complexes.
Parce que sa distance moyenne du noyau détermine l’énergie d’un électron, chaque orbitale atomique avec un ensemble donné de nombres quantiques a une énergie particulaire qui lui est associée, l’énergie orbitale.
\
Dans les atomes o\(r\) ions avec un seul électron, toutes les orbitales avec la même valeur de \(n\) ont la même énergie (elles sont dégénérées), et les énergies des principales coquilles augmentent de façon régulière lorsque \(n\) augmente. Un atome o\(r\) ion avec le ou les électrons dans la ou les orbitales de plus basse énergie est dit être dans son état fondamental, tandis qu’un atome o\(r\) ion dans lequel un o\(r\) plus d’électrons occupent des orbitales de plus haute énergie est dit être dans un état excité.
Contributeurs et attributions
-
Modifié par Joshua Halpern (Howard University)
.