Comme le contrôleur P-Only, l’algorithme proportionnel-intégral (PI) calcule et transmet un signal de sortie de contrôleur (CO) à chaque temps d’échantillonnage, T, à l’élément de contrôle final (par exemple, une vanne, une pompe à vitesse variable). Le CO calculé par l’algorithme PI est influencé par les paramètres de réglage du contrôleur et l’erreur du contrôleur, e(t).
Les contrôleurs PI ont deux paramètres de réglage à ajuster. Bien que cela les rende plus difficiles à régler qu’un contrôleur P-Only, ils ne sont pas aussi complexes que le contrôleur PID à trois paramètres.
L’action intégrale permet aux contrôleurs PI d’éliminer l’offset, une faiblesse majeure d’un contrôleur P-only. Ainsi, les contrôleurs PI offrent un équilibre entre complexité et capacité qui en fait de loin l’algorithme le plus utilisé dans les applications de contrôle de processus.
L’algorithme PI
Alors que différents vendeurs coulent ce qui est essentiellement le même algorithme sous différentes formes, nous explorons ici ce qui est diversement décrit comme la forme dépendante, idéale, continue, de position :
![]()
Où :
CO = signal de sortie du contrôleur (le fil de sortie)
CObias = biais du contrôleur ou valeur nulle ; réglé par transfert sans à-coups comme expliqué ci-dessous
e(t) = erreur actuelle du contrôleur, définie comme SP – PV
SP = point de consigne
PV = variable de processus mesurée (le fil d’entrée)
Kc = gain du contrôleur, un paramètre de réglage
Ti = temps de réinitialisation, un paramètre de réglage
Les deux premiers termes à droite du signe égal sont identiques au contrôleur P-Only référencé en haut de cet article.
Le mode intégral du contrôleur est le dernier terme de l’équation. Sa fonction est d’intégrer ou de sommer continuellement l’erreur du contrôleur, e(t), au cours du temps.
Certaines choses que nous devrions savoir sur le paramètre de réglage du temps de réinitialisation, Ti:
| ▪ | Il fournit un poids séparé au terme intégral de sorte que l’influence de l’action intégrale peut être ajustée indépendamment. |
| ▪ | Il se trouve dans le dénominateur de sorte que les valeurs plus petites fournissent un poids plus important à (c’est-à-dire. augmenter l’influence de) le terme intégral. |
| ▪ | Il a des unités de temps donc il est toujours positif. |
Fonction du terme proportionnel
Comme pour le contrôleur P-Only, le terme proportionnel du contrôleur PI, Kc-e(t), ajoute ou soustrait à CObias en fonction de la taille de l’erreur du contrôleur e(t) à chaque instant t.
Lorsque e(t) augmente ou diminue, la quantité ajoutée à CObias augmente ou diminue immédiatement et proportionnellement. L’histoire passée et la trajectoire actuelle de l’erreur du contrôleur n’ont aucune influence sur le calcul du terme proportionnel.
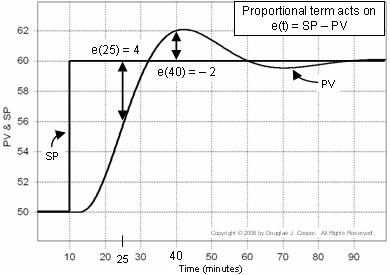
Le tracé ci-dessous (cliquez pour une vue agrandie) illustre cette idée pour une réponse à un point de consigne. L’erreur utilisée dans le calcul proportionnel est indiquée sur le tracé :
▪ Au temps t = 25 min, e(25) = 60-56 = 4
▪ Au temps t = 40 min, e(40) = 60-62 = -2
Rappelant que l’erreur du contrôleur e(t) = SP – PV, plutôt que de considérer PV et SP comme des traces séparées comme nous le faisons ci-dessus, nous pouvons calculer et tracer e(t) à chaque point du temps t.
Vous trouverez ci-dessous (cliquez pour une vue agrandie) les données identiques à celles ci-dessus, sauf qu’elles sont refondues comme un tracé de e(t) lui-même. Remarquez que dans le tracé ci-dessus, PV = SP = 50 pour les 10 premières min, alors que dans le tracé de l’erreur ci-dessous, e(t) = 0 pour la même période.
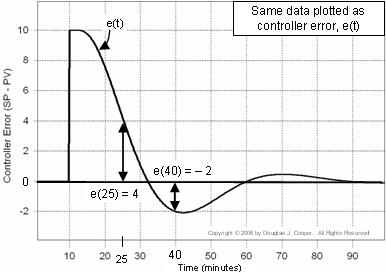
Ce tracé est utile car il nous aide à visualiser comment l’erreur du contrôleur change continuellement de taille et de signe au fil du temps.
Fonction du terme intégral
Alors que le terme proportionnel considère la taille actuelle de e(t) uniquement au moment du calcul du contrôleur, le terme intégral considère l’historique de l’erreur, ou la durée et la distance de la variable de processus mesurée par rapport au point de consigne au fil du temps.
L’intégration est une addition continue. L’intégration de l’erreur dans le temps signifie que nous additionnons l’historique complet des erreurs du contrôleur jusqu’au moment présent, en commençant par le moment où le contrôleur a été commuté pour la première fois en automatique.
L’erreur du contrôleur est e(t) = SP – PV. Dans le tracé ci-dessous (cliquez pour une vue agrandie), la somme intégrale de l’erreur est calculée comme les zones ombrées entre les traces SP et PV.
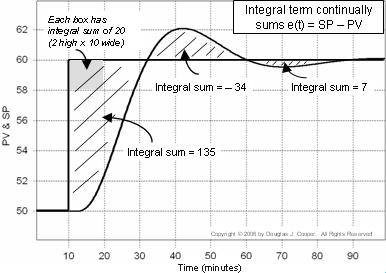
Chaque boîte du tracé a une somme intégrale de 20 (2 de haut par 10 de large). Si nous comptons le nombre de boîtes (y compris les fractions de boîtes) contenues dans les zones ombrées, nous pouvons calculer la somme intégrale de l’erreur.
Donc, lorsque la PV franchit pour la première fois la consigne vers t = 32, la somme intégrale a augmenté d’environ 135. Nous écrivons le terme intégral du contrôleur PI comme:
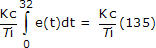
Puisque c’est l’erreur du contrôleur qui dirige le calcul, nous obtenons une vue directe de la situation à partir d’un graphique d’erreur du contrôleur comme indiqué ci-dessous (cliquez pour une grande vue):

Notez que l’intégrale de chaque partie ombrée a le même signe que l’erreur. Comme la somme intégrale commence à s’accumuler lorsque le régulateur est mis en automatique pour la première fois, la somme intégrale totale croît tant que e(t) est positive et se réduit lorsqu’elle est négative.
Au temps t = 60 min sur les tracés, la somme intégrale est de 135 – 34 = 101. La réponse est en grande partie réglée au temps t = 90 min, et la somme intégrale est alors 135 – 34 + 7 = 108.
L’action intégrale élimine le décalage
La phrase précédente fait une observation subtile mais très importante. La réponse est en grande partie terminée au temps t = 90 min, et pourtant la somme intégrale de toutes les erreurs n’est pas nulle.
Dans cet exemple, la somme intégrale a une valeur finale ou résiduelle de 108. C’est cette valeur résiduelle qui permet à l’action intégrale du contrôleur PI d’éliminer l’offset.
Comme nous l’avons vu dans un article précédent, la plupart des processus sous contrôle P-only subissent un offset pendant le fonctionnement normal. L’offset est une valeur soutenue pour l’erreur du contrôleur (c’est-à-dire que PV n’est pas égal à SP à l’état stable).
Nous reconnaissons du contrôleur P-Only :
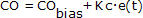
que CO sera toujours égal à CObias à moins que nous y ajoutions ou soustrayions quelque chose.
La seule façon dont nous avons quelque chose à ajouter ou à soustraire de CObias dans l’équation P-Only ci-dessus est si e(t) n’est pas zéro. Si e(t) n’est pas stable à zéro, alors PV n’est pas égal à SP et nous avons un décalage.
Cependant, avec le contrôleur PI:
![]()
nous savons maintenant que la somme intégrale de l’erreur peut avoir une valeur finale ou résiduelle après qu’une réponse soit terminée. Ceci est important car cela signifie que e(t) peut être zéro, et pourtant nous pouvons toujours avoir quelque chose à ajouter ou à soustraire de CObias pour former la sortie finale du contrôleur, CO.
Donc, tant qu’il y a une erreur (tant que e(t) n’est pas zéro), le terme intégral augmentera ou diminuera en taille pour avoir un impact sur CO. Les changements de CO ne cesseront que lorsque PV sera égal à SP (lorsque e(t) = 0) pendant une période de temps soutenue.
À ce moment-là, le terme intégral peut avoir une valeur résiduelle comme nous venons de le voir. Cette valeur résiduelle de l’intégration, lorsqu’elle est ajoutée à CObias, crée essentiellement une nouvelle valeur de biais globale qui correspond au nouveau niveau de fonctionnement.
En effet, l’action intégrale réinitialise continuellement la valeur de biais pour éliminer le décalage lorsque le niveau de fonctionnement change.
Défis de la commande PI
L’emploi de l’algorithme PI présente des défis :
| ▪ | Les deux paramètres de réglage interagissent entre eux et leur influence doit être équilibrée par le concepteur. |
| ▪ | Le terme intégral tend à augmenter le comportement oscillatoire ou de roulement de la réponse du processus. |
Parce que les deux paramètres de réglage interagissent l’un avec l’autre, il peut être difficile d’arriver aux « meilleures » valeurs de réglage. La valeur et l’importance de notre recette de conception et de réglage augmentent à mesure que le contrôleur devient plus complexe.
Initialisation du contrôleur pour le transfert sans bosses
Lorsque nous faisons passer n’importe quel contrôleur du mode manuel au mode automatique (de la boucle ouverte à la boucle fermée), nous voulons que le résultat soit sans incident. C’est-à-dire que nous ne voulons pas que la commutation provoque des actions de contrôle brusques qui ont un impact sur notre processus ou le perturbent
Nous obtenons ce résultat souhaité lors de la commutation en initialisant la somme intégrale des erreurs du contrôleur à zéro. De plus, le point de consigne et la valeur du biais du contrôleur sont initialisés en réglant :
▪ SP égal à la PV actuelle
▪ CObias égal au CO actuel
Avec la somme intégrale de l’erreur réglée à zéro, il n’y a rien à ajouter ou à soustraire de CObias qui causerait un changement soudain dans la sortie actuelle du contrôleur. Avec le point de consigne égal à la variable de processus mesurée, il n’y a pas d’erreur pour entraîner un changement dans notre CO. Et avec le biais du contrôleur réglé sur notre valeur de CO actuelle, nous sommes préparés par défaut à maintenir le fonctionnement actuel.
Ainsi, lorsque nous passons du mode manuel au mode automatique, nous avons un « transfert sans à-coups » sans surprise. C’est un résultat que tout le monde apprécie.
Temps de réinitialisation vers le taux de réinitialisation
Différents fournisseurs coulent leurs algorithmes de contrôle sous des formes légèrement différentes. Certains utilisent la bande proportionnelle plutôt que le gain du contrôleur. De même, certains utilisent le taux de réinitialisation, Tr, au lieu du temps de réinitialisation. Ceux-ci sont simplement l’inverse les uns des autres :
Tr = 1/Ti
Quoi qu’il en soit de la façon dont les paramètres de réglage sont exprimés, les algorithmes PI sont tous également capables.
Mais il est essentiel de connaître votre fabricant avant de commencer à régler votre contrôleur car les valeurs des paramètres doivent être adaptées à votre forme particulière d’algorithme.Les logiciels commerciaux de conception et de réglage des contrôleurs aborderont automatiquement ce problème pour vous.
Mise en œuvre d’un contrôleur PI
Nous explorons la conception, le réglage et la mise en œuvre des contrôleurs PI sur l’échangeur de chaleur dans cet article et sur les réservoirs drainés par gravité dans cet article.