Une asymptote est une ligne qu’un graphique approche, mais ne coupe pas.
Dans cette leçon, nous apprendrons à trouver les asymptotes verticales, les asymptotes horizontales et les asymptotes obliques (obliques) des fonctions rationnelles.
Thèmes connexes :
Plus de leçons sur le calcul

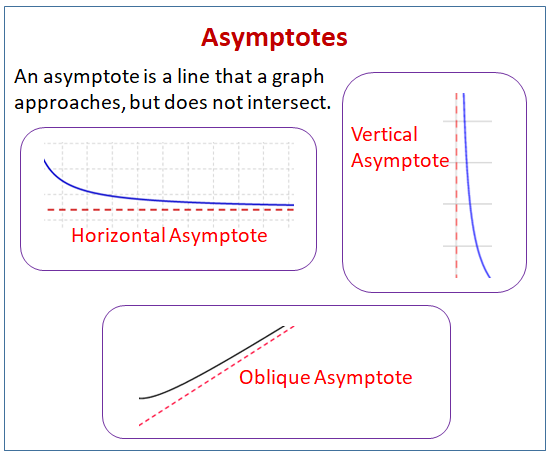
Le diagramme suivant montre les différents types d’asymptotes : asymptotes horizontales, asymptotes verticales et asymptotes obliques. Faites défiler la page pour plus d’exemples et de solutions sur la façon de trouver des asymptotes.

Comment déterminer l’asymptote verticale?

Méthode 1 : Utilisez la définition de l’asymptote verticale

La ligne x = a est appelée une asymptote verticale de la courbe y = f(x) si au moins une des déclarations suivantes est vraie.

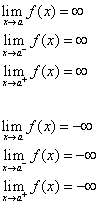
Méthode 2 :

Pour les fonctions rationnelles, les asymptotes verticales sont des lignes verticales qui correspondent aux zéros du dénominateur.
Donné la fonction rationnelle, f(x)

Etape 1 : écrire f(x) sous forme réduite

Etape 2 : si x – c est un facteur du dénominateur alors x = c est l’asymptote verticale.

Exemple :

Trouver les asymptotes verticales de

Solution :

Méthode 1 : utiliser la définition de l’asymptote verticale.

Si x est proche de 3 mais plus grand que 3, alors le dénominateur x – 3 est un petit nombre positif et 2x est proche de 8. Donc, est un grand nombre positif.

Intuitivement, on voit que

De même, si x est proche de 3 mais plus petit que 3, alors x – 3 est un petit nombre négatif et 2x est proche de 8. Donc, est un grand nombre négatif.

La droite x = 3 est l’asymptote verticale.

Méthode 2:

Etape 1 : f(x) est déjà sous forme réduite.

Etape 2 : Le dénominateur est x – 3, et donc l’asymptote verticale est en x = 3.

Trouver les asymptotes verticales des fonctions rationnelles

Ce qu’il faut rechercher, pour trouver les asymptotes verticales des fonctions rationnelles.

• Afficher les solutions pas à pas

Asymptotes verticales des fonctions rationnelles : Manière rapide de les trouver

Exemple de recherche des asymptotes verticales des fonctions rationnelles.

• Afficher les solutions pas à pas

Comment trouver les asymptotes verticales des fonctions rationnelles

• Afficher les solutions pas à pas

Comment déterminer l’asymptote horizontale ?

Méthode 1 : utiliser la définition de l’Asymptote horizontale

La droite y = L est appelée une asymptote horizontale de la courbe y = f(x) si soit

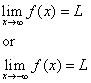
Méthode 2 :

Pour la fonction rationnelle, f(x)

Si le degré de x au numérateur est inférieur au degré de x au dénominateur alors y = 0 est l’asymptote horizontale.

Si le degré de x au numérateur est égal au degré de x au dénominateur alors y = c où c est obtenu en divisant les coefficients de tête.

Exemple :

Trouver les asymptotes horizontale et verticale de la fonction.

Solution :

Méthode 1 :

Diviser le numérateur et le dénominateur par x.

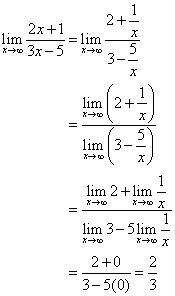
La ligne est l’asymptote horizontale.

Méthode 2 :

Le degré de x au numérateur est égal au degré de x au dénominateur.

En divisant les coefficients de tête, on obtient

La droite est l’asymptote horizontale.

Courci pour trouver les asymptotes horizontales des fonctions rationnelles

Un couple d’astuces qui rendent la recherche des asymptotes horizontales des fonctions rationnelles très facile à faire

• Afficher les solutions pas à pas

Cette vidéo donnera un aperçu de base des asymptotes horizontales. Nous déterminerons si les fonctions rationnelles données ont des asymptotes horizontales et ce qu’elles sont.

• Afficher les solutions étape par étape

Cette vidéo entrera plus en détail dans les règles des asymptotes horizontales.

• Afficher les solutions étape par étape

Asymptote oblique ou asymptote oblique

Certaines courbes ont des asymptotes obliques, c’est-à-dire ni horizontales ni verticales.

Si alors la droite y = mx + b est appelée asymptote oblique ou oblique car les distances verticales entre la courbe y = f(x) et la droite y = mx + b approchent de 0.

Pour les fonctions rationnelles, les asymptotes obliques se produisent lorsque le degré du numérateur est supérieur d’un degré à celui du dénominateur. Dans ce cas, l’équation de l’asymptote oblique peut être trouvée par division longue.

Exemple :

Trouver les asymptotes de la fonction

Solution :

Puisque le dénominateur x2 + 1 n’est jamais 0, il n’y a pas d’asymptote verticale.

Puisque le degré de x au numérateur est supérieur au degré de x au dénominateur, il n’y a pas d’asymptote horizontale.

Puisque le degré de x au numérateur est supérieur de un au degré de x au dénominateur, nous pouvons utiliser la division longue pour obtenir l’asymptote oblique.

Donc, la droite y = x est l’asymptote oblique.

Formation d’asymptotes obliques de fonctions rationnelles

Cette vidéo décrit quand une fonction rationnelle a une asymptote oblique, décrit brièvement ce qu’est une asymptote oblique, puis fait deux exemples.

• Afficher les solutions pas à pas

Trouver les asymptotes d’une fonction rationnelle (verticales, horizontales et obliques)

Cette vidéo montre comment trouver les asymptotes verticales et une asymptote oblique / oblique d’une fonction rationnelle.

• Afficher les solutions pas à pas

Trouver toutes les asymptotes d’une fonction rationnelle (verticale, horizontale, oblique / oblique)

Nous examinons ici une fonction et trouvons l’asymptote verticale et concluons également qu’il n’y a pas d’asymptotes horizontales, mais qu’une asymptote oblique existe. Nous utilisons alors la division longue pour trouver l’asymptote oblique.

• Montrer les solutions étape par étape

Essayez la calculatrice gratuite Mathway et le résolveur de problèmes ci-dessous pour pratiquer divers sujets mathématiques. Essayez les exemples donnés, ou tapez votre propre problème et vérifiez votre réponse avec les explications étape par étape.