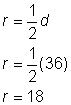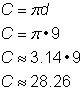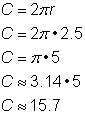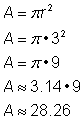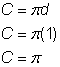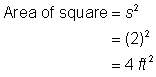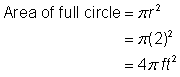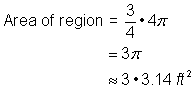Cercles
Objectif(s) d’apprentissage :
– Identifier les propriétés des cercles.
– Trouver la circonférence d’un cercle.
– Trouver l’aire d’un cercle.
– Trouver l’aire et le périmètre de figures géométriques composées.
Introduction
Les cercles sont une forme commune. On en voit partout – les roues d’une voiture, les frisbees qui passent dans l’air, les disques compacts qui délivrent des données. Ce sont tous des cercles.
Un cercle est une figure bidimensionnelle tout comme les polygones et les quadrilatères. Cependant, les cercles sont mesurés différemment de ces autres formes – vous devez même utiliser certains termes différents pour les décrire. Jetons un coup d’œil à cette forme intéressante.
Propriétés des cercles
Un cercle représente un ensemble de points, qui sont tous à la même distance d’un point fixe et central. Ce point fixe est appelé le centre. La distance du centre du cercle à n’importe quel point du cercle s’appelle le rayon.
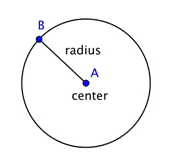
Lorsque deux rayons (le pluriel de rayon) sont mis ensemble pour former un segment de ligne à travers le cercle, vous avez un diamètre. Le diamètre d’un cercle passe par le centre du cercle et a ses extrémités sur le cercle lui-même.
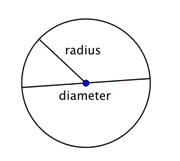
Le diamètre d’un cercle quelconque est deux fois la longueur du rayon de ce cercle. Il peut être représenté par l’expression 2r, ou « deux fois le rayon ». Ainsi, si vous connaissez le rayon d’un cercle, vous pouvez le multiplier par 2 pour trouver le diamètre ; cela signifie également que si vous connaissez le diamètre d’un cercle, vous pouvez le diviser par 2 pour trouver le rayon.
|
Exemple |
||
|
Problème |
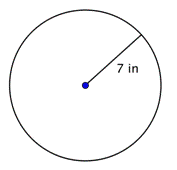
Trouver le diamètre du cercle.
|
|
|
d = 2r d = 2(7) d = 14 |
Le diamètre est égal à deux fois le rayon, soit 2r. Le rayon de ce cercle est de 7 pouces, donc le diamètre est 2(7) = 14 pouces. |
|
|
Réponse |
Le diamètre est de 14 pouces. |
|
|
Exemple |
||
|
Problème |
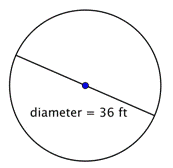
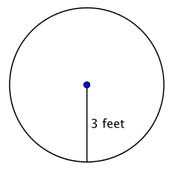
Trouver le rayon du cercle.
|
|
|
|
Le rayon est la moitié du diamètre, soit |
|
|
Réponse |
Le rayon est de 18 pieds. |
|
Circonférence
La distance autour d’un cercle est appelée la circonférence. (Rappelons que la distance autour d’un polygone est le périmètre.)
Une propriété intéressante des cercles est que le rapport entre la circonférence d’un cercle et son diamètre est le même pour tous les cercles. Quelle que soit la taille du cercle, le rapport de la circonférence et du diamètre sera le même.
Certaines mesures réelles de différents articles sont fournies ci-dessous. Les mesures sont précises au millimètre ou au quart de pouce près (selon l’unité de mesure utilisée). Regardez le rapport entre la circonférence et le diamètre pour chacun d’eux – bien que les articles soient différents, le rapport pour chacun est approximativement le même.
|
Item |
Circonférence (C) (arrondie au centième le plus proche) |
.
Diamètre (d) |
Ratio |
|
Bonnet |
253 mm . |
79 mm |
|
|
Quarter |
84 mm |
27 mm |
|
|
Bowl |
37.25 in |
11.75 in |
|
La circonférence et le diamètre sont des mesures approximatives, car il n’y a pas de moyen précis de mesurer ces dimensions exactement. Cependant, si vous étiez en mesure de les mesurer plus précisément, vous constateriez que le rapport ![]() se rapprocherait de 3,14 pour chacun des éléments donnés. Le nom mathématique du rapport
se rapprocherait de 3,14 pour chacun des éléments donnés. Le nom mathématique du rapport ![]() est pi, et est représenté par la lettre grecque
est pi, et est représenté par la lettre grecque ![]() .
.
![]() est une décimale non terminale et non répétitive, il est donc impossible de l’écrire complètement. Les 10 premiers chiffres de
est une décimale non terminale et non répétitive, il est donc impossible de l’écrire complètement. Les 10 premiers chiffres de ![]() sont 3,141592653 ; ils sont souvent arrondis à 3,14 ou estimés sous la forme de la fraction
sont 3,141592653 ; ils sont souvent arrondis à 3,14 ou estimés sous la forme de la fraction ![]() . Notez que 3,14 et
. Notez que 3,14 et ![]() sont tous deux des approximations de
sont tous deux des approximations de![]() , et sont utilisés dans des calculs où il n’est pas important d’être précis.
, et sont utilisés dans des calculs où il n’est pas important d’être précis.
Puisque vous savez que le rapport de la circonférence au diamètre (ou ![]() ) est cohérent pour tous les cercles, vous pouvez utiliser ce nombre pour trouver la circonférence d’un cercle si vous connaissez son diamètre.
) est cohérent pour tous les cercles, vous pouvez utiliser ce nombre pour trouver la circonférence d’un cercle si vous connaissez son diamètre.
![]() =
= ![]() , donc C =
, donc C = ![]() d
d
Aussi, puisque d = 2r, alors C = ![]() d =
d = ![]() (2r) = 2
(2r) = 2![]() r.
r.
Circonférence d’un cercle
Pour trouver la circonférence (C) d’un cercle, utilisez l’une des formules suivantes :
Si vous connaissez le diamètre (d) d’un cercle : ![]()
Si vous connaissez le rayon (r) d’un cercle : ![]()
|
Exemple |
||
|
Problème |
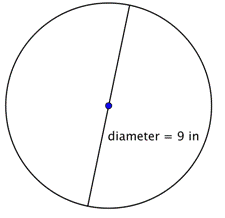
Déterminez la circonférence du cercle.
|
|
|
|
Pour calculer la circonférence étant donné un diamètre de 9 pouces, utilisez la formule Puisque vous utilisez une approximation pour |
|
|
Réponse |
La circonférence est de 9 |
|
|
Exemple |
||
|
Problème |
Trouver la circonférence d’un cercle dont le rayon est de 2.5 yards. |
|
|
|
Pour calculer la circonférence d’un cercle dont le rayon est de 2,5 yards, utilisez la formule |
|
|
Réponse |
La circonférence est de 5 |
|
Un cercle a un rayon de 8 pouces. Quelle est sa circonférence, arrondie au pouce le plus proche?
A) 25 pouces
B) 50 pouces
C) 64 pouces2
D) 201 pouces
L’aire
![]() est un nombre important en géométrie. Vous l’avez déjà utilisé pour calculer la circonférence d’un cercle. Vous utilisez également
est un nombre important en géométrie. Vous l’avez déjà utilisé pour calculer la circonférence d’un cercle. Vous utilisez également ![]() lorsque vous calculez l’aire d’un cercle.
lorsque vous calculez l’aire d’un cercle.
Aire d’un cercle
Pour trouver l’aire (A) d’un cercle, utilisez la formule : ![]()
|
Exemple |
||
|
Problème |
Trouve l’aire du cercle.
|
|
|
|
Pour trouver l’aire de ce cercle, utilisez la formule N’oubliez pas d’écrire la réponse en termes d’unités carrées, puisque vous trouvez l’aire. |
|
|
Réponse |
L’aire est de 9 |
|
Un bouton a un diamètre de 20 millimètres. Quelle est l’aire du bouton ? Utilisez 3.14 comme approximation de ![]() .
.
A) 62,8 mm
B) 314 mm2
C) 400 mm2
D) 1256 mm2
Figures composées
Maintenant que vous savez comment calculer la circonférence et l’aire d’un cercle, vous pouvez utiliser ces connaissances pour trouver le périmètre et l’aire de figures composées. L’astuce pour résoudre ce type de problèmes est d’identifier les formes (et les parties de formes) dans la figure composite, de calculer leurs dimensions individuelles, puis de les additionner.
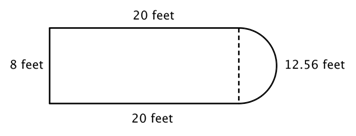
Par exemple, regardez l’image ci-dessous. Est-il possible de trouver le périmètre ?
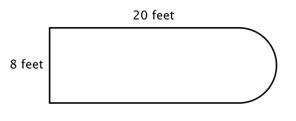
La première étape consiste à identifier des figures plus simples dans cette figure composite. Vous pouvez la décomposer en un rectangle et un demi-cercle, comme indiqué ci-dessous.
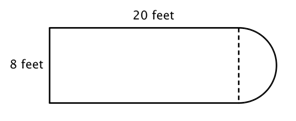
Vous savez comment trouver le périmètre d’un rectangle, et vous savez comment trouver la circonférence d’un cercle. Ici, le périmètre des trois côtés pleins du rectangle est de 8 + 20 + 20 = 48 pieds. (Notez que seulement trois côtés du rectangle s’ajouteront au périmètre de la figure composée parce que l’autre côté n’est pas à un bord ; il est couvert par le demi-cercle !)
Pour trouver la circonférence du demi-cercle, utilisez la formule ![]() avec un diamètre de 8 pieds, puis prenez la moitié du résultat. La circonférence du demi-cercle est
avec un diamètre de 8 pieds, puis prenez la moitié du résultat. La circonférence du demi-cercle est ![]() , soit environ 12,56 pieds, donc le périmètre total est d’environ 60,56 pieds.
, soit environ 12,56 pieds, donc le périmètre total est d’environ 60,56 pieds.
|
Exemple |
||
|
Problème |
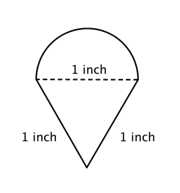
Trouve le périmètre (au centième près) de la figure composée, constituée d’un demi-cercle et d’un triangle.
|
|
|
|
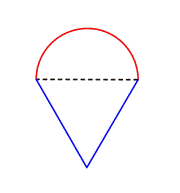
Identifier les formes plus petites dans la figure composée. Cette figure contient un demi-cercle et un triangle. |
|
|
Diamètre (d) = 1
Circonférence du demi-cercle = |
Trouvez la circonférence du cercle. Puis divisez par 2 pour trouver la circonférence du demi-cercle. |
|
|
|
|
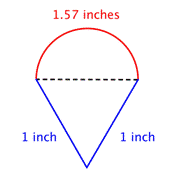
Déterminez le périmètre total en ajoutant la circonférence du demi-cercle et les longueurs des deux jambes. Puisque notre mesure de la circonférence du demi-cercle est approximative, le périmètre sera également une approximation. |
|
Réponse |
Approximativement 3.57 pouces |
|
|
Exemple |
||
|
Problème |
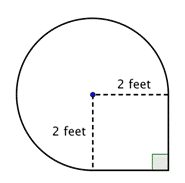
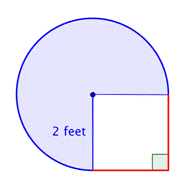
Trouver l’aire de la figure composée, composée des trois quarts d’un cercle et d’un carré, au centième près.
|
|
|
|
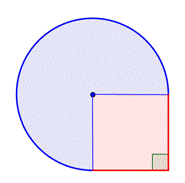
Identifier les formes plus petites dans la figure composite. Cette figure contient une région circulaire et un carré. Si vous trouvez l’aire de chacune, vous pouvez trouver l’aire de la figure entière. |
|
|
|
Trouvez l’aire du carré. |
|
|
|
|
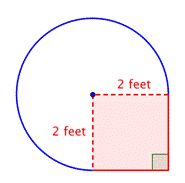
Trouve l’aire de la région circulaire. Le rayon est de 2 pieds. Notez que la région est |
|
|
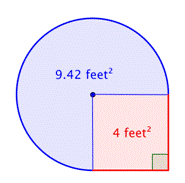
4 pieds2 + |
Ajoutez les deux régions ensemble. Puisque votre mesure de l’aire du cercle est approximative, l’aire de la figure sera également une approximation. |
|
Réponse |
L’aire est d’environ 13.42 pieds2. |
|
Quelle est l’aire (au centième près) de la figure représentée ci-dessous ? (Les deux régions arrondies sont des demi-cercles.)
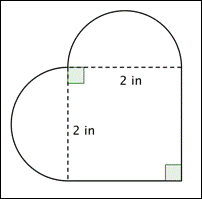
A) 16,56 po2
B) 7,14 po2
C) 4 in2
D) 3,14 in2
Summary
Les cercles sont une forme géométrique importante. La distance autour d’un cercle est appelée la circonférence, et l’espace intérieur d’un cercle est appelé l’aire. Le calcul de la circonférence et de l’aire d’un cercle nécessite un nombre appelé pi (![]() ), qui est une décimale non terminale et non répétitive. Pi est souvent approximé par les valeurs 3,14 et
), qui est une décimale non terminale et non répétitive. Pi est souvent approximé par les valeurs 3,14 et ![]() . Vous pouvez trouver le périmètre ou l’aire de formes composées – y compris les formes qui contiennent des sections circulaires – en appliquant les formules de circonférence et d’aire lorsque cela est approprié.
. Vous pouvez trouver le périmètre ou l’aire de formes composées – y compris les formes qui contiennent des sections circulaires – en appliquant les formules de circonférence et d’aire lorsque cela est approprié.